一種由粗到細的脈壓雷達信號調制類型識別方法*

李 利，紀 凱，柴娟芳

（1海軍大連艦艇學院，遼寧大連 116018；2上海機電工程研究所，上海 200233）

0 引言

脈壓雷達信號的脈內調制方式識別是脈壓雷達脈內特征分析的第一個主要組成部分，它是根據脈內調制方式實現有針對性脈內調制參數估計的重要前提[1]。因此，脈內調制方式識別作為脈內特征分析的重要組成，對現代雷達電子對抗中新型反輻射導彈導引頭的脈壓雷達信號的識別、截獲與跟蹤具有重要的現實意義。

脈內調制方式識別隸屬于無線電信號調制識別范疇，國內外在這方面的研究還沒有獲得特別公認的有效方法，而且大部分集中在通信信號的調制方式識別上面[2－3]。文中通過分析普通雷達信號CW（common waveform）、PSK（phase shift keying）信號、LFM（linear frequency modulation）信號和 NLFM（nonlinear frequency modulation）信號的調制特征，從這些信號的時頻域調制特征入手，提出了一種從粗到細的調制方式識別方法。所謂由粗到細是指首先對信號進行粗類型識別，即先將信號分成PSK信號和調頻信號兩大類，PSK信號包括二相編碼（BPSK）信號、四相編碼（QPSK）信號和普通雷達信號（PSK信號相位無跳變的特例），調頻信號包括LFM信號和NLFM信號，然后使用時域累加瞬時自相關法實現了PSK信號的類內細分，采用一次瞬時自相關實現了調頻信號的類內細分，仿真實驗證實了算法具有優良的識別性能。

1 算法原理

文中研究的脈壓信號包括2PSK、QPSK、LFM信號和NLFM信號[4－5]。PSK信號的表達式可以寫成：

其中：a（t）為信號包絡，φ（t）為相位調制函數，φ0為初相。M 為PSK信號的編碼形式。M ＝2為2PSK，φ（t）有0，π兩個取值；M ＝4為QPSK，φ（t）有0四個取值。

調頻信號的表達式可以寫為：

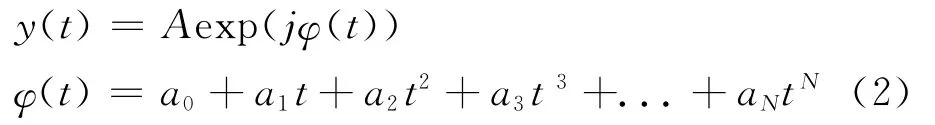
當N＝2時為LFM信號，當N＝3時為文中研究的NLFM信號。它們的幅度歸一化頻譜形狀可以由圖1表示。

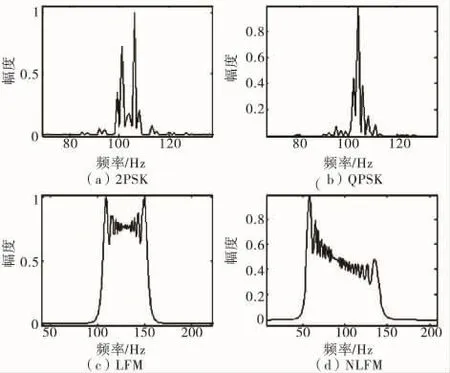
圖1 脈壓雷達信號的幅度歸一化頻譜

從上述信號的頻譜特征可以看出，PSK信號的功率譜呈現出沖擊型的三角形外形特征，帶寬較窄，而調頻信號的功率譜呈現出類似矩形的外形特征，具有一定的帶寬，利用這個特點，通過測信號的帶寬，然后設定一個閾值，可以很容易將信號分成PSK信號和調頻信號兩類。

由于PSK信號的頻譜包含連續譜和離散譜兩部分，加之噪聲的影響，直接估計信號的帶寬并不容易。在此，采用了首先對頻譜進行多點平滑，然后估算信號3dB帶寬的方法來估計信號的帶寬。下式為信號功率譜全序列頻域平滑公式[6]：

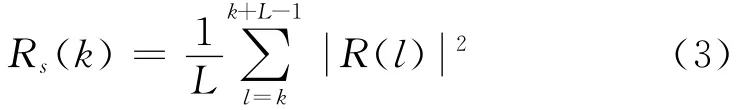
式中：R（l）為接收信號r（t）的頻譜，L為平滑窗寬度。通過對接收信號的功率譜進行平滑處理，可以在較低信噪比條件下對信號的中心頻率進行有效估計。

設Rs（k）最大的幅度值為Rs（k0），搜索Rs（k）中大于0.5Rs（k0）的所有譜線，這些譜線所占的帶寬即為信號的3dB帶寬。由信號的3dB帶寬，根據事先設定的閾值，可以很容易實現粗分類。同時，對PSK信號，可以計算3dB帶寬內頻譜的重心：

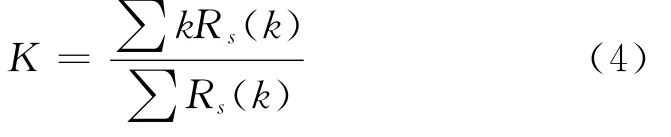
式中k為所有滿足Rs（k）中大于0.5Rs（k0）的譜線序號。則利用平滑后的功率譜重心得到載頻的粗估計值為：

式中：m為FFT點數，T為采樣間隔。

此處，已經實現了信號的粗分類，下面對信號進行細分類。對兩類信號進行細分類，均采用了瞬時自相關的方法，通過觀察瞬時自相關后PSK信號的時域波形和調頻信號瞬時自相關后的功率譜，就可以實現兩類信號的類內細分類。首先分析PSK信號的類內細分：

設下面的PSK信號：

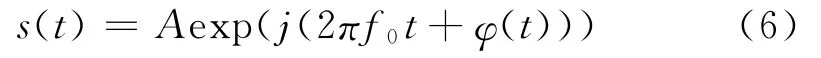
式中：A為常數，f0為信號載頻，φ（t）為相位調制函數。對信號延遲τ，有：

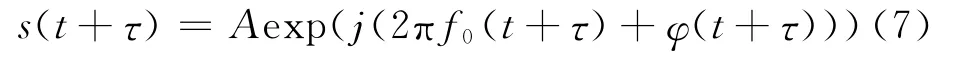
式（6）與式（7）的共軛相乘得：

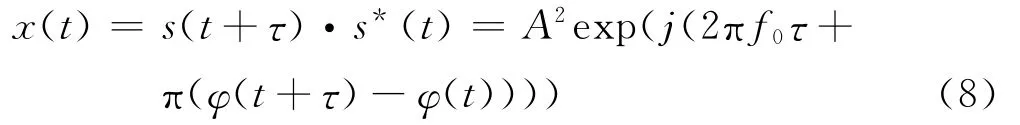
上式稱為信號的瞬時自相關。為了消除相位偏移量2πf0τ的影響，需要首先估計信號的載頻。而信號的載頻估計已經由上面給出為f′0，Δf0＝f′0－f0為載頻估計誤差。然后抵消掉相位偏移量，如下式：

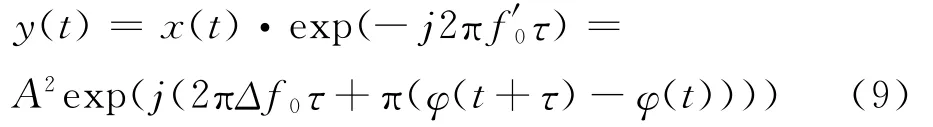
在載頻估計足夠準確的情況下，估計誤差近似為0，不考慮幅值，上式可以近似等于：

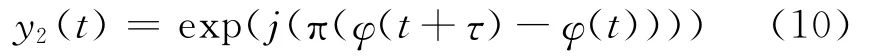
對于BPSK信號，當不存在相位跳變時，上式的取值為＋1，當存在相位跳變時，上式取值為－1。對于QPSK信號，跳變處的幅值會增加一個0跳變值，通過觀察式（10）的時域波形跳變點的幅度，可以實現PSK信號的類內細分。

由于相位的變化對噪聲比較敏感，所以式（10）的抗噪能力不強。為了改善上述方法的低信噪比性能，采用了時域累加瞬時自相關的方法。假設信號s（t）到信號s（t＋τ）發生相位突變，那么依次增大τ（τ＜T（碼元周期）），分別取不同的τ值，多次運算，然后時域疊加，由于相位突變點從同一時刻開始，因此相互疊加而增強，提高了抗噪性能。時間延遲此處取等間隔τ，上述過程離散形式可表示為：

式中：k為自然數，L為疊加次數。

其次分析調頻信號的類內細分：

對于三階PPS（多項式相位信號），即文中討論的NLFM信號，可以表示為：

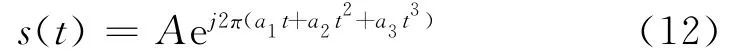
對信號做瞬時自相關得：

由于τ為固定值，上式退化為一個LFM信號，其功率譜密度將呈現近似矩形的外形特征。如果信號s（t）為LFM信號，此時a3＝0，上式將退化為一個單載頻信號，其功率譜密度在頻域表現為一根沖擊譜線，因此，通過觀察調頻信號在瞬時自相關后的功率譜，可以實現LFM和NLFM的調制類型細分類。

綜上所述，文中提出的由粗到細的脈壓雷達信號調制方式識別算法識別過程總結如下：

1）對信號做FFT計算信號的功率譜；

2）對功率譜進行多點平滑，計算3dB帶寬和功率譜重心；

3）設定閾值，根據3dB帶寬將信號粗分為PSK信號和調頻信號兩類，并根據功率譜重心計算PSK信號的載頻；

4）使用載頻估計值抵消PSK信號的相位偏移，然后計算時域累加瞬時自相關，根據時域波形的跳變幅值可以實現普通雷達信號、BPSK信號和QPSK信號的細分類；

5）計算調頻信號的瞬時自相關，然后做FFT計算功率譜密度，如果是近似矩形的功率譜外形則為NLFM信號，如果是沖擊譜線，則為LFM信號。

2 仿真實驗

選取5種典型參數脈壓雷達信號進行仿真實驗，參數如下：

采樣頻率100MHz。普通雷達信號：載頻20MHz；BPSK信號：碼字[1 0 1 0 0 1 0]，載頻20MHz；QPSK信號：碼字[0 2 1 3 0 2 0]，載頻20MHz；LFM 信號：a0＝0，a1＝2×107，a2＝1.0×1012；NLFM信號：a0＝0，a1＝1.0×107，a2＝0.8×1012，a3＝0.8×1017。采樣點數均為512點，信噪比為6dB。計算結果如圖2～圖4所示，圖2和圖3中從左到右從上至下分別為LFM、NLFM、BPSK和QPSK所對應的波形。由于普通雷達信號在自相關以后時域波形無幅度突變，很容易被識別出來，故文中沒有畫出普通雷達信號的波形。

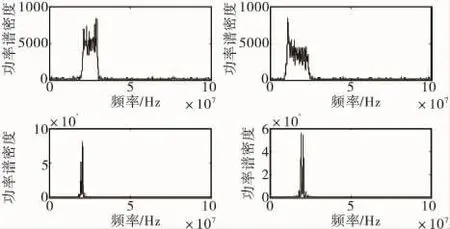
圖2 脈壓雷達信號的功率譜（SNR＝6dB）

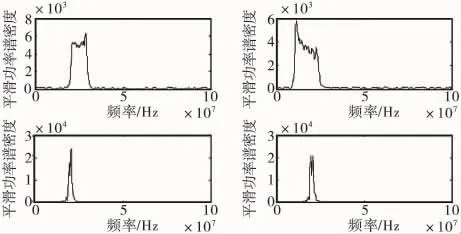
圖3 脈壓雷達信號的平滑功率譜（SNR＝6dB）

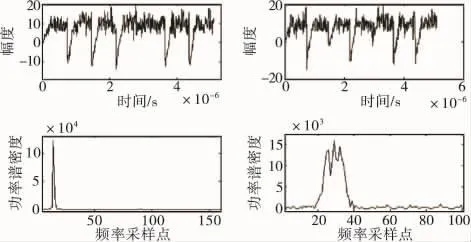
圖4 調制方式識別結果（SNR＝6dB）

通過觀察平滑后的脈壓雷達信號功率譜可以發現，調頻信號的帶寬要明顯大于PSK信號的帶寬，通過這一點可以很容易實現信號的粗類型識別。圖4中上面一行為BPSK和QPSK信號10次累加瞬時自相關的結果，延遲時間從2個采樣點到20個采樣點，步長為2，共10次，此時要注意最大延遲要小于碼元周期。通過觀察時域波形可得，BPSK相關結果的幅值只有10，－10兩種，而QPSK相關結果幅值有10，0，－10三種，而普通雷達信號相關結果幅值只有10一種，通過這一點可以實現PSK信號的細分類。

圖4下面一行為LFM和NLFM信號一次瞬時自相關后的功率譜波形。LFM信號瞬時自相關后將變成單載頻信號，其功率譜會在2a2τ處呈現沖擊波形，而NLFM信號一次瞬時自相關后將變成LFM信號，其功率譜將呈現類似矩形的外形特征，如圖所示，通過這一點，LFM信號和NLFM信號被區分開來。此時對延遲τ的取值要注意，τ取值過小會使NLFM自相關后得到的LFM信號帶寬過小，導致信號不容易區分，而τ取值過大，會使可用的采樣點數變少，導致FFT后的頻譜不夠準確，此處綜合考慮選取的τ值為128個采樣點。

圖5畫出了識別成功率與信噪比的關系曲線，包括粗類型識別成功率與信噪比的關系、PSK類內識別成功率與信噪比的關系（10次累加瞬時自相關時）和調頻信號類內識別成功率與信噪比的關系。信噪比從－6dB到6dB，步長2dB，每條曲線仿真實驗次數100次。

圖5 識別成功率與信噪比的關系

從曲線圖中可以看出，粗類型識別的性能最好，FM識別次之，PSK識別算法的抗噪聲能力最差。這是因為前面二者都使用了FFT算法，而FFT算法具有良好的抗噪聲性能，而PSK識別時域算法的突變點很容易被噪聲干擾，雖然采用了時域累積的方法在一定程度上增強了抗噪性能，但是效果有限，并沒有獲得根本性的性能改善，這種方法雖然有缺陷，但是它計算簡單，方便有效，在6dB時可以達到將近100%的識別成功率，具有很高的工程應用價值。

3 結論

文中分析了普通雷達信號、PSK信號、LFM信號和NLFM信號的調制特征，從這些信號的時頻域調制特征入手，提出了一種從粗到細的調制方式識別方法，首先將信號分成PSK信號和調頻信號兩大類，然后實現了信號的類內細分。仿真實驗表明，該算法計算簡單，方便有效，在6dB時可以達到將近100%的識別成功率，具有很高的工程應用價值。

[1]Roome S J.Classification of radar signals in modulation domain[J].Electronics Letters，1992，28（8）：704－705.

[2]李楊，李國通，楊根慶.通信信號數字調制方式自動識別算法研究[J].電子與信息學報，2005，27（2）：197－201.

[3]Hsue Z S，Soliman S S.Automatic modulation classification using zero crossing[J].Radar and Signal Processing，IEE Proceedings F，1990，137（6）：459－464.

[4]張群逸.雷達中的相位編碼信號與處理[J].火控雷達技術，2005，34（4）：30－32.

[5]李利，司錫才，彭巧樂.一種綜合時頻分布在mc－PPS檢測中的應用[J].大連海事大學學報，2009，35（1）：39－42.

[6]鄧振淼，劉渝，楊姍姍.多相碼雷達信號調制方式識別[J].數據采集與處理，2008，23（3）：265－269.