捷聯姿態系統的誤差分配算法設計＊

陳 辭，高洪宇，張崇猛，舒東亮

（1海軍駐大連造船廠軍事代表室，遼寧大連 116005；2天津航海儀器研究所，天津 300131）

0 引言

在純慣導狀態下，由于存在加速度計誤差和陀螺誤差，捷聯慣導系統的姿態誤差存在較大幅值震蕩，難以滿足長時間提供較高精度姿態的需求。因此，為了提高系統的性價比，需要加入外部參考速度信息，構成捷聯式羅經姿態系統，將姿態誤差抑制在一定范圍內，從而長時間提供高精度的姿態信息。在系統的研制階段，需要對慣性元件和測速裝置的誤差引起的系統姿態誤差進行分析，并確定所研制系統需要采用慣性元件和測速裝置的精度，即進行誤差分配[1]。

平臺式羅經系統已非常成熟，其通過在水平回路和方位回路中引入阻尼環節，調整對陀螺的控制量，從而使平臺精確的保持水平和航向。利用與其此相同的原理，在水平回路計算和方位回路計算過程中引入阻尼環節，可使捷聯式慣性導航系統處于羅經工作狀態，長時間提供精度較高的姿態信息。目前已有精度較高的捷聯羅經姿態系統研制完成并得到大量使用，如法國的 Octans[2－3]，該系統使用的陀螺為光纖陀螺。

1 捷聯慣導系統的誤差

捷聯慣導系統的誤差方程與平臺式慣導系統的誤差方程是等效的[4]。如式（1）所示[5]：

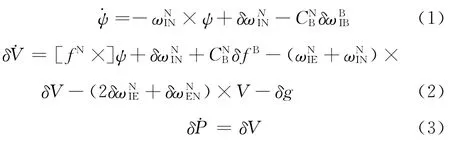
式中：ψ為姿態誤差；δV為速度誤差；δg為重力加速度誤差；δP為位置誤差；I表示慣性坐標系；E表示地球坐標系；N表示當地地理坐標系；B表示載體坐標系。

式（1）中的陀螺組件誤差δωBIB包括陀螺常漂、標度誤差、安裝誤差和隨機誤差，其可用等效到地理坐標系的陀螺漂移表示，如式（4）所示。同樣，加速度計組件誤差δfB包括加速度計零偏、標度誤差、安裝誤差和隨機誤差，其也可用等效到地理坐標系的加速度計零偏表示，如式（5）所示。

根據上述誤差方程，可得捷聯慣導系統的誤差框圖如圖1所示。Ω為地球自轉角速率；φ為當地維度；R為地球半徑；g為地球重力加速度。圖中省略了垂向通道的誤差計算。

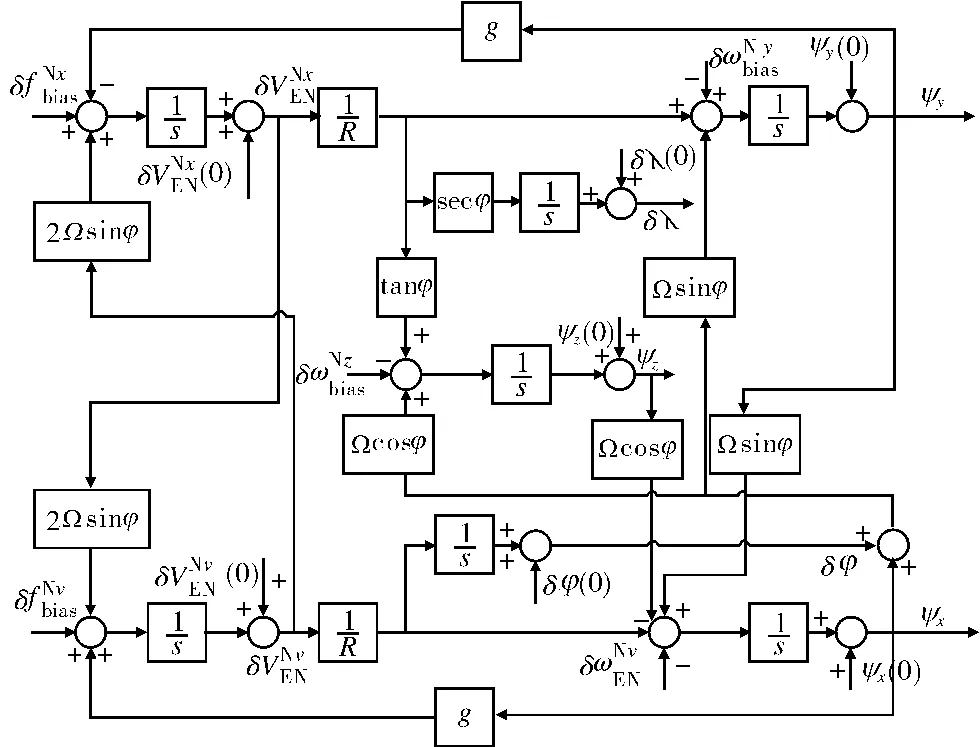
圖1 捷聯慣導系統的誤差框圖

2 羅經回路及其誤差分析

如圖1所示，在北向水平回路中，存在著由航向角誤差引起的等效陀螺漂移ψzΩcosφ，從而引起東向水平姿態誤差ψx的變化，這種影響稱為羅經效應。利用羅經效應，通過設計適當的阻尼網絡，將東向水平姿態誤差引入航向角計算環節，形成羅經回路，從而減小航向角誤差，使系統輸出在一定誤差范圍內的航向。同樣，在東向水平回路中加入阻尼環節，也可使系統輸出在一定誤差范圍內的水平姿態。羅經回路及水平回路中阻尼網絡的設計與平臺式阻尼網絡的設計原理和方法相同[6]。

加入阻尼網絡后羅經系統東向水平回路的誤差框圖如圖2所示，羅經回路的誤差方框圖如圖3所示。圖2所示為多輸入單輸出系統，圖3所示為多輸入多輸出系統。系統對準后，處于穩定狀態，因此系統的誤差主要由穩態誤差決定。

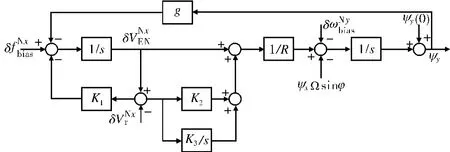
圖2 系統東向水平回路的誤差框圖

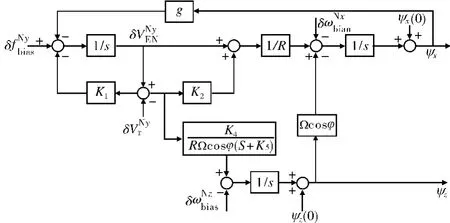
圖3 系統羅經回路的誤差框圖

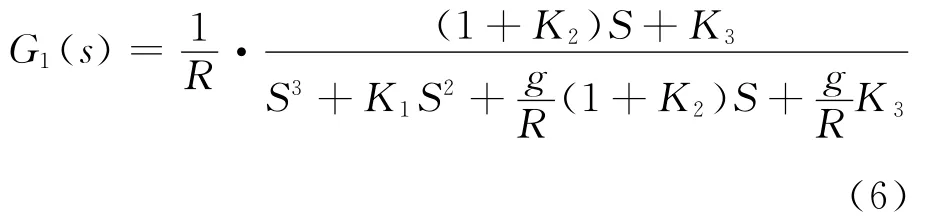
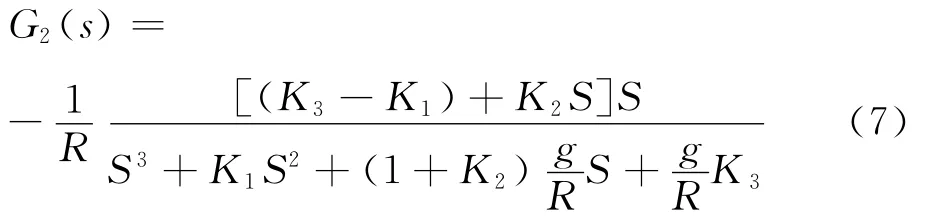
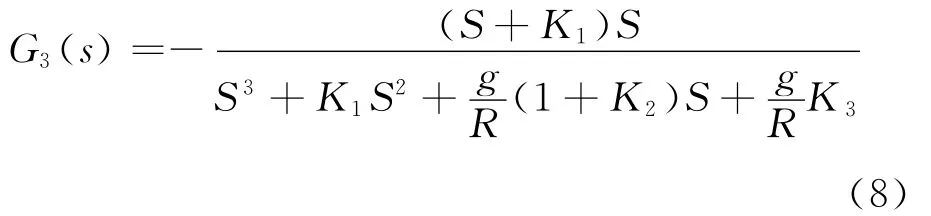
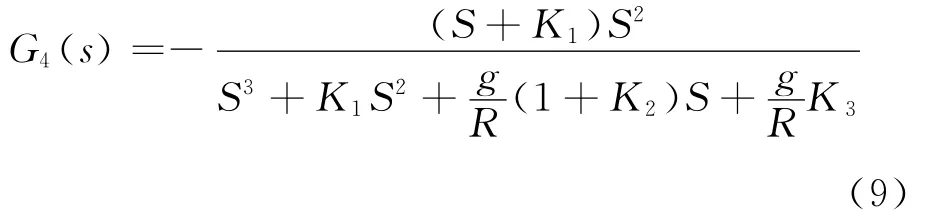
式（6）傳遞函數為0型系統，式（7）和式（8）為Ⅰ型系統，式（9）為 Ⅱ 型系統。因此，在穩態條件下，ψy僅與δ有關。即：

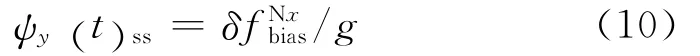
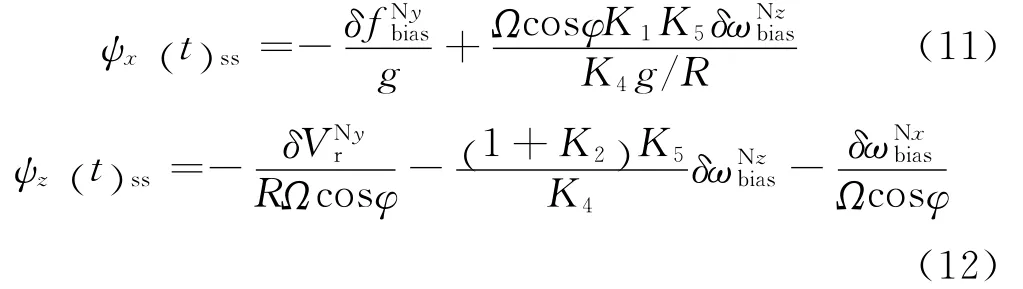
在羅經回路中，適當的選擇K2、K4和K5后，的影響很小，可以忽略。

經上述分析，對于采用羅經方式的捷聯姿態系統，穩態下其水平姿態誤差主要由加速度計的零偏決定，成一定的比例關系；航向誤差主要由東向陀螺漂移和北向參考速度誤差決定。

3 仿真結果

在捷聯姿態系統中采用羅經方案，針對現有陀螺和加速度計的性能進行了動態仿真。陀螺誤差如表1所示，加速度計誤差如表2所示，系統搖擺條件如表3所示。仿真的緯度為39.183°，航向45°，參 考 速 度 誤 差0.2kn，導航時間為8h。系統姿態角誤差的仿真結果如圖4、圖5和圖6所示。最大姿態誤差如表4所示。

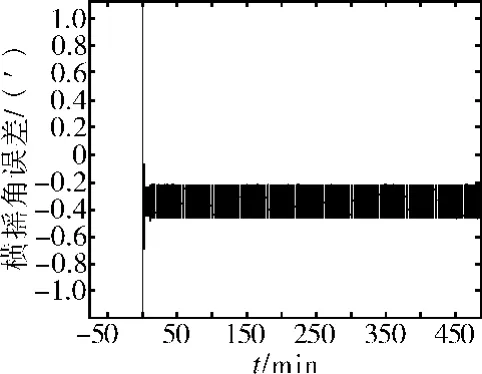
圖4 橫搖角誤差

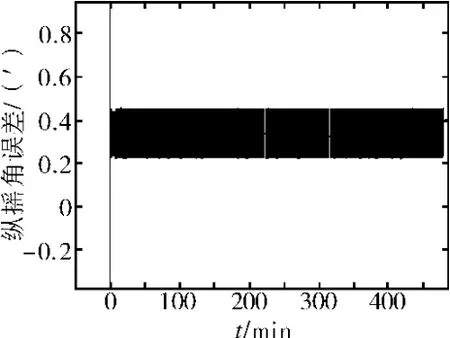
圖5 縱搖角誤差

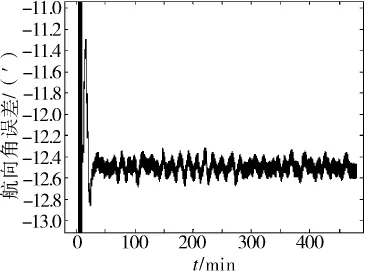
圖6 航向角誤差

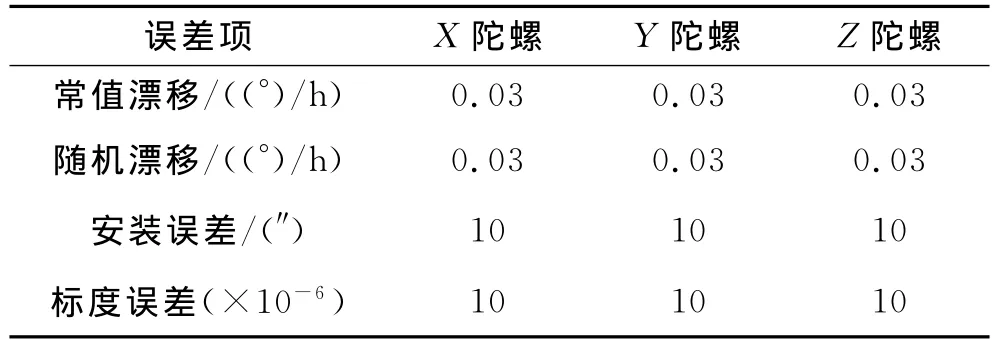
表1 陀螺組件誤差

表2 加表組件誤差

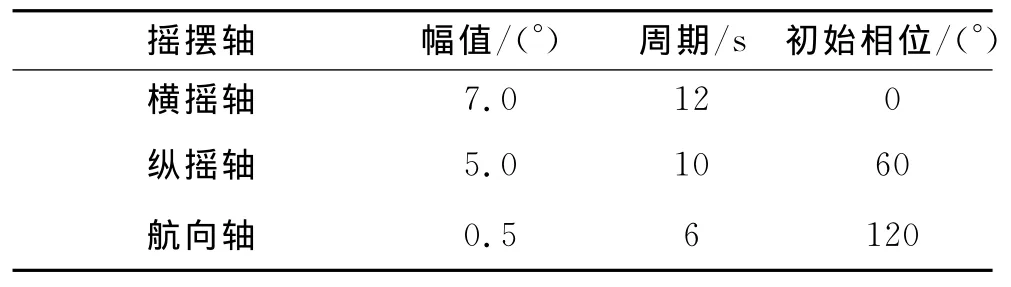
表3 系統搖擺規律

表4 系統最大姿態誤差

4 結論

在東向水平通道和航向通道中加入阻尼環節，系統工作在羅經狀態下，系統的姿態信息可以抑制在較小的誤差范圍內。在穩定狀態下，北向水平姿態誤差僅與東向加速度計零偏有關，東向水平姿態誤差僅與北向加速度計零偏和天向陀螺漂移有關，其中主要起作用的是加速度計零偏；航向角誤差僅與北向參考速度誤差、天向陀螺漂移和東向陀螺漂移有關，其中主要起作用的是北向參考速度和東向陀螺漂移。通過計算機仿真可以看出針對捷聯姿態系統中采用羅經方案設計的姿態誤差分配算法的正確性。

[1]James E Kain，James R Cloutier.Rapid transfer alignment for tactical weapon applications[C]//Proceedings of AIAA Guidance，Navigation and Control Conference，1989：1290－1300.

[2]T Gaiffe，Y Cottreau，N Faussot，et al.Marine fiberoptic gyrocompass with integral motion sensor[C]//DGON 99，Stuttgart，15.0－15.7.

[3]T Gaiffe，Y Cottreau，N Faussot，et al.Highly compact fiber optic gyrocompass for applications at depth up to 3000meters[C]//Underwater Technology，2000，UT 00.Proceedings of the 2000International Symposium，2000：155－160.

[4]Weinred A，Bar－Itzhack I Y.The Psi－angle error equation in strapdown inertial navigation systems[J].IEEE Transaction on Aerospace and Electronic Systems，1978，AES－14（3）：539－542.

[5]D H Titterton，J L Weston.Strapdown inertial navigation technology[M].London：Peter Peregrinus Ltd.，1997：119－147.

[6]黃德鳴，程祿.慣性導航系統[M].北京：國防工業出版社，1992：107－150.