基于單軸旋轉的捷聯系統誤差特性分析＊

孫 偉，孫 楓

（1遼寧工程技術大學測繪與地理科學學院，遼寧阜新 123000；2哈爾濱工程大學自動化學院，哈爾濱150001）

0 引言

長時間工作的捷聯慣導系統，慣性測量元件的常值偏差將引起隨時間積累的定位誤差，它是影響慣性導航系統性能的重要因素[1－2]，將慣性測量單元（inertial measurement unit，IMU）進行轉動以調制慣性器件常值偏差是實現高精度慣性導航的有效方法之一[3－5]，但是IMU的連續轉動會激發出新的誤差因素[6]，引起系統定位誤差。因此，文中針對轉臺轉軸與當地垂線偏離及尺寸效應這兩個誤差因素對旋轉捷聯系統導航精度的影響進行分析與仿真。

1 IMU單軸旋轉捷聯系統誤差抑制原理

捷聯慣導系統單軸旋轉自動補償方法[7－9]是將安裝有慣性器件的IMU相對載體坐標系（b坐標系，oxbybzb）旋轉，使慣性器件的偏差沿著載體坐標系呈周期性變化。設oxsyszs為IMU坐標系，s坐標系是隨著IMU位置改變而改變的一個時變坐標系。

設初始時刻IMU坐標系與載體坐標系重合，然后s系以角速度ω繞ozb軸旋轉。采用地理坐標系作為導航坐標系。圖1是以IMU單軸旋轉為例說明自動補償原理。

在t時刻，載體坐標系和IMU坐標系的夾角為ωt，兩個坐標系之間的關系用方向余弦表示[10]：

圖1 IMU坐標系與載體坐標系的相對位置關系

慣性器件的輸出誤差中一般包括常值偏差和隨機偏差，常值偏差可以通過標定的方法進行補償，但是這種常值偏差也呈現出變化的趨勢，主要體現在逐次啟動誤差和逐日變化的誤差，因此通過標定的方法不能將慣性器件的常值偏差進行完全的補償。假設標定結束后陀螺儀和加速度計的誤差模型為[11]：

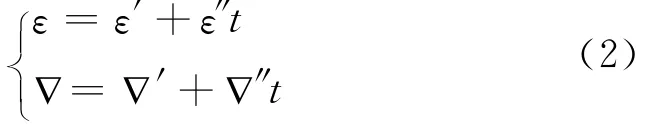
式中：ε′、?′分別表示陀螺儀和加速度計剩余常值誤差；ε″、?″分別表示陀螺儀和加速度計與系統工作時間相關的誤差系數。

根據IMU旋轉過程中s坐標系與b坐標系的相對位置關系，得到載體系下慣性器件偏差的調制形式：

由式（3）和式（4）可以看出，水平方向上慣性器件的剩余常值偏差被調制成周期變化的量，在一個轉動周期內經過積分后為零，與時間有關的項經過積累后為常值，因此ozb軸引起的誤差將隨時間積累。除了慣性器件自身的誤差因素外，旋轉捷聯慣導系統中轉臺轉軸與當地垂線偏離及尺寸效應誤差是影響導航精度的主要因素，下文圍繞這兩種誤差對導航精度的影響機理進行分析。

2 轉臺轉軸與當地垂線偏離

以單軸旋轉為例，分析轉臺的轉動軸與當地垂線存在夾角時對導航精度的影響。轉臺傾斜角的大小及傾斜角的方向具有任意性，為便于分析及不失一般性，假定α為轉臺平面與載體平面的夾角，β為平臺傾斜取向與地理東向的夾角，得到旋轉過程中s坐標系相對b系的位置關系，如圖2所示。

根據圖2描述的b系相對s系的位置關系，可以得到兩個坐標系之間的關系用方向余弦Tsb表示：

圖2 IMU旋轉過程中s系與b系的相對位置

由于轉臺轉動軸與地垂線不重合，在IMU的旋轉過程中，3個陀螺儀均敏感到地球自轉角速度在s坐標系上的分量；水平加速度計敏感到重力加速度在s坐標系水平方向上的分量：

如圖2所示，s坐標系到b坐標系的轉動過程：

其中，兩坐標系的轉換關系可以用如下轉換矩陣表示：

將式（8）和式（9）分別代入式（10），經過化簡得到陀螺儀和加速度計的輸出在載體系下的表示形式：

由式（12）可以看出，轉臺轉軸與當地垂線偏離導致旋轉角速度和方位陀螺漂移在水平方向上產生常值分量，水平方向上的陀螺儀敏感此分量。捷聯矩陣Tnb的微分方程及Tnb與陀螺儀輸出的函數關系分別如下：

通過對式（12）分析可得，在平臺傾斜取向一定的條件下，臺面傾角α越大，旋轉角速度的水平分量越大，系統積累的誤差就越大。加速度計的偏差在水平方向上產生投影，使水平方向上的均值不為零，即轉動后加速度計的水平常值漂移得到部分調制。為了定性分析轉臺轉軸與當地垂線偏離時引起的系統誤差，忽略由于陀螺儀輸出的變化導致捷聯矩陣更新時產生的變化，即假定＝I。則經過時間t′，IMU旋轉過程中加速度計的輸出經過積分得到水平速度誤差為：

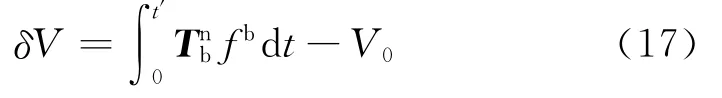
V0表示載體理想狀態下的水平速度，其值為零。在水平通道內：

由式（17）可以看出，與時間有關的三角函數項經過一個周期的積分后為零，但是反映在速度上，引起速度的周期性波動，周期為IMU的旋轉周期；由于旋轉機構的轉動軸與地垂線偏離，方位陀螺儀漂移在水平方向上產生分量，導致速度誤差表現為隨時間持續增長。

3 尺寸效應誤差

當加速度計偏離理想位置和IMU處于轉動狀態時，離心加速度和切向加速度的存在引起加速度計的測量誤差。加速度計輸出誤差的表達式為[12]：

式中第一項表示切向加速度的影響，第二項表示向心加速度的影響。

由于IMU安裝在載體上，假設IMU坐標系和b坐標系具有同一個水平面，此時不用考慮IMU方位軸上加速度計的尺寸效應。將兩個水平加速度計構成一個測量組件，可得到慣性測量組件的尺寸效應誤差為：

如圖3，對于每個加速度計的位置矢量rp能分解為兩個分量r和dp，r是IMU坐標系上的加速度計組件中心p的位置矢量；dp是加速度計ax相對于IMU坐標原點的位置矢量，因此有：

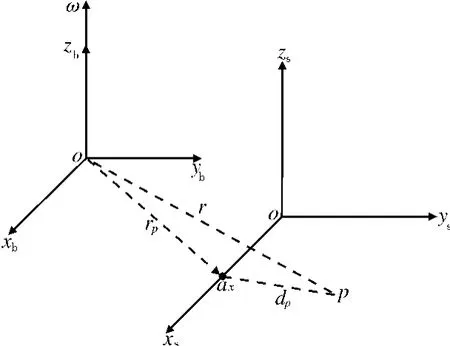
圖3 尺寸效應幾何分析圖

式（21）代入式（20）：

式（22）中第一項是由于r不等于零引起的，稱為“慣性測量組件的安裝偏差尺寸效應”用?m表示；第二項是由于dp不等于零引起的，稱為“加速度計的尺寸效應”用?e表示。其中慣性測量組件的安裝偏差可以通過在線標定補償，文中主要討論IMU連續轉動過程中加速度計尺寸效應產生的影響，假定水平方向上的加速度計到IMU坐標原點的距離均為dp，則加速度計的輸出表示為：

IMU轉動過程中，旋轉角速度的不平穩導致水平加速度計輸出是一個帶有隨機振蕩的量。為便于分析問題，假設載體始終處于靜止狀態，有Tnb＝I得到導航系下加速度值為：

水平加速度計偏差在一個完整的周期內完全得到調制，與旋轉角速度有關的項由于伴隨有隨機量導致一個周期內不能完全得到調制，因此旋轉角速度在水平方向上產生了不對稱的常值，通過對加速度的積分得到載體速度誤差和位置誤差。

4 仿真分析

為驗證轉臺轉軸與當地垂線偏離及尺寸效應誤差對旋轉捷聯系統導航精度的影響，利用VC＋＋開發工具構建這兩種條件下的捷聯慣性導航系統模擬器及解算過程，根據仿真結果驗證上述兩種誤差因素對系統導航精度的影響。

4.1 轉臺轉軸與當地垂線偏離仿真

仿真條件：靜基座導航，初始地理位置為北緯45.7796°、東經126.6705°，轉臺轉軸與當地垂線夾角為0.001°，為了問題分析的簡單化，傾斜角取向為沿導航坐標系東西向。IMU旋轉角速度為6°／s，加速度零位誤差10－4g，暫不考慮陀螺漂移和其它誤差因數，仿真時間24h。

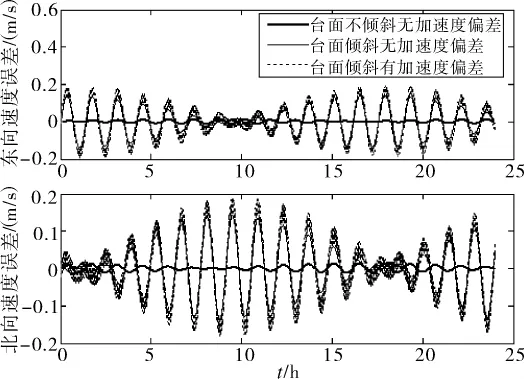
圖4 IMU旋轉過程中不同條件下系統水平速度誤差曲線

下面對圖4進行分析。理論上講，根據式（17），當轉臺傾角取向沿導航系東西方向，由傾角取向定義得β＝0°，在一個旋轉周期內方位陀螺漂移得到積累，引起北向速度產生常值誤差；加速度計零位偏差在一個轉動周期內得到調制，但是引起速度誤差的周期振蕩。仿真結果驗證了這一點：無加速度計零位偏差時，臺體傾斜導致水平速度產生舒勒周期和傅科周期振蕩；在轉臺平面傾斜的條件下，無加速度零位偏差導致系統中不產生旋轉周期，有加速度零位偏差導致舒勒周期中存在旋轉周期。

圖5 IMU旋轉過程中不同條件下系統位置誤差曲線

旋轉角速度在導航坐標系oxb軸上的投影被東向陀螺感知，這一分量引起常值經度誤差，如圖5所示。為了直觀反映出載體在不同誤差條件下的定位精度，根據定位誤差計算公式（25）計算出不同時刻系統的位置誤差，如圖6所示。

式中：R 表示地球半徑；L 表 示當地緯度；λ表示當地經度。經對比發現：同轉臺轉軸與當地垂線重合時相比，偏離時會引起定位誤差，達到0.12nmile以上；在轉軸與地垂線偏離的條件下，通過對比定位誤差可以看出：與沒有加速度計偏差時的定位誤差相比，有加速度計偏差時產生的定位誤差多出0.02nmile，驗證了式（14）的正確性。

圖6 IMU旋轉過程中不同條件下系統定位誤差曲線

4.2 尺寸效應誤差仿真

仿真條件：IMU轉動角速度6°／s，轉速誤差為10－5，加速度計到坐標原點的距離為0.1m，初始位置同4.1，不考慮任何其它誤差因素。

圖7 有無尺寸效應時載體姿態誤差曲線

圖8 有無尺寸效應時載體定位誤差曲線

IMU轉動過程中，尺寸效應引起的向心加速度參與慣導解算導致水平姿態角產生常值偏差，轉動角速度的不平穩同時引起陀螺儀的輸出是非對稱的，在一個轉動周期不能將其完全調制，導致姿態誤差加劇；轉速的不平穩同時引起加速度計的輸出在導航系上的分量不能得到完全調制，如式（20），激發出導航系統的位置誤差。如圖8所示，24h的仿真過程中最大可以達到0.06nmile，大于無尺寸效應時的導航誤差。

5 結論

文中概述了旋轉捷聯慣導系統的誤差抑制機理，分別針對轉臺轉軸與當地垂線偏離、尺寸效應對系統導航精度的影響進行了理論推導、分析與仿真。通過對比仿真結果可以看出當轉臺轉軸與當地垂線偏離時產生了0.14nmile的定位誤差，遠大于轉軸與地垂線重合時的位置誤差；雖然尺寸效應引起的定位誤差遠小于轉軸與地垂線偏離所引起的定位誤差，但是轉動角速度的不平穩仍然會激發出0.06nmile的位置誤差。目前旋轉式捷聯慣導系統處于實驗室階段，如何設計合理的誤差補償措施是本實驗室下一步的主要工作。

[1]于旭東，王宇，張鵬飛，等.單軸旋轉對慣性導航系統誤差特性的影響[J].中國慣性技術學報，2008，16（6）：643－648.

[2]Ishibashi S，Tsukioka S，Sawa T.The rotation control system to improve the accuracy of an inertial navigation system installed in an autonomous underwater vehicle[C]// Workshop on Scientific Use of Submarine Cables and Related Technologies 2007，2007：495－498.

[3]Morrow R B，Heckman D W.High precision IFOG insertion into the strategic submarine navigation system[C]//IEEE 1998Position Location and Navigation Symposium，1998：332－338.

[4]Levinson E，Willcocks M.The next generation marine inertial navigation is here now[C]//IEEE Position Location and Navigation Symposium，1994：121－127.

[5]孫楓，孫偉.旋轉捷聯慣導系統精對準技術研究[J].系統工程與電子技術，2010，32（3）：630－633.

[6]黃昆，王戈，楊功流，等.旋轉式捷聯慣導系統的誤差特性分析[C]//中國慣性技術學會第六屆學術年會論文集，2008：56－61.

[7]袁保侖，饒谷音.光學陀螺旋轉慣導系統原理探討[J].國防科技大學學報，2006，28（6）：76－80.

[8]孫楓，孫偉.旋轉自動補償捷聯慣導系統技術研究[J].系統工程與電子技術，2010，32（1）：122－125.

[9]孫楓，孫偉，郭真.基于IMU旋轉的捷聯慣導系統自補償方法[J].儀器儀表學報，2009，30（12）：2511－2517.

[10]孫楓，孫偉.搖擺基座下旋轉捷聯系統粗對準技術研究[J].儀器儀表學報，2010，31（4）：929－936.

[11]劉峰，徐策，尚克軍，等.水平初始對準誤差對旋轉IMU導航系統的精度影響[J].中國慣性技術學報，2008，16（6）：649－656.

[12]張樹俠，孫靜.捷聯式慣性導航系統[M].北京：國防工業出版社，1992.