恒速下旋轉葉片同步振動辨識方法

歐陽濤，段發階，李孟麟，孔祥洪

(天津大學精密測試技術及儀器國家重點實驗室，天津 300072)

旋轉機械廣泛應用于航空、電力、能源工業等部門，主要包括航空發動機、燃氣輪機、煙氣輪機、汽輪機等．旋轉葉片作為旋轉機械的核心部件，對旋轉機械的安全運行起到關鍵性作用．旋轉葉片的振動測量是旋轉機械的一個重要研究領域．目前，葉尖定時非接觸旋轉葉片測振技術已得到廣泛研究和應用，為旋轉機械的狀態監測和故障診斷提供可靠依據．

葉尖定時(blade tip timing，BTT)測振的基本原理[1-4]是將葉尖定時傳感器沿徑向安裝在旋轉機械相對靜止的殼體上，利用傳感器感受在它前面通過的旋轉葉片所產生的脈沖信號來記錄葉片到來的時刻．由于葉片的振動，葉片的端部相對于轉動方向將會向前或向后偏移，使得葉片每次到達傳感器的實際時間與無振動時的期望值不相等，即脈沖到達時間t會隨著葉片的振動發生改變，通過不同的分析算法對該信號序列｛t｝進行處理，可得到葉片同步共振、異步顫振等參數信息，進而對旋轉機械的運行狀況做出準確評價．

針對葉片不同的運行狀態和振動形式，基于葉尖定時原理的葉片振動辨識方法主要有用于辨識異步振動的多傳感器均布法、“5＋2” 分布法、差頻法等[5-6]，用于辨識同步振動的速矢端跡法[7]、雙參數法[8]、自回歸法[9-10]等．速矢端跡法和雙參數法主要是通過變速掃頻方式測量同步振動，自回歸法應用范圍有限．針對恒速下葉片同步振動特點，本文提出一種多傳感器倍頻遍歷辨識算法，采用4 支以上任意分布的葉尖定時傳感器準確辨識出葉片同步振動參數，并能夠對葉片同步振動信號進行有效恢復．

1 葉尖定時同步振動欠采樣模型

根據葉尖定時測振原理，在轉軸上安裝一支轉速同步傳感器ZT，在葉片頂端機殼上分布一支或多支葉尖定時傳感器TIP，如圖1 所示．經過葉尖定時處理系統，每支傳感器可獲得葉片經過時的振動位移序列{y}．轉子每旋轉一周，同一葉片經過每支傳感器各一次，即相當于每支傳感器以轉速頻率?為采樣頻率對葉片振動位移信號進行采樣．由于葉片振動頻率ω一般遠大于轉子的轉速頻率，不滿足Nyquist采樣定理，葉尖定時測振方法屬于嚴重的欠采樣，僅僅通過一支或幾支傳感器是很難直接還原出葉片的振動信號．

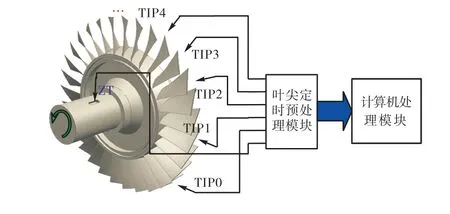
圖1 葉尖定時測振系統示意Fig.1 BTT system schematic

葉片振動模型方程為

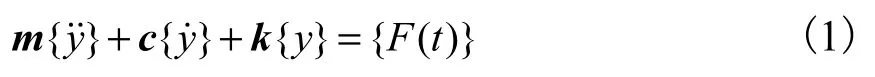
式中：m為質量矩陣；c為阻尼矩陣；k為剛度矩陣；{F(t)}為隨時間t變化的外界激振力．任意時刻葉片振動可以寫成多個諧波疊加形式

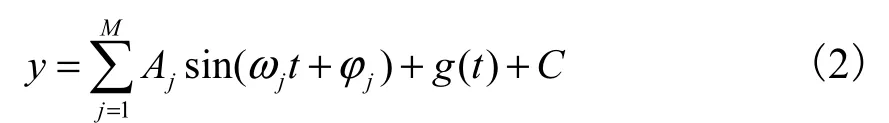
式中：諧波數量M≥1；y為振動位移；Aj為各諧波幅值；φj為各諧波初始相位；g(t)為獨立白噪聲；C為葉片振動平衡位置可能產生的常偏量．

恒速下，葉片發生同步振動時，葉片振動頻率是轉速頻率的整數倍，即ω＝Ne×?，Ne為自然數，稱為振動倍頻，一般與葉片振動激勵源分布及激勵諧波成分有關．考慮單頻占優的同步振動成分

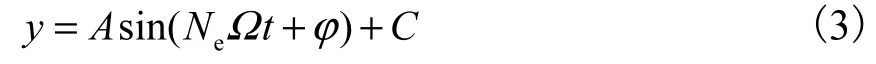
葉片每周到達各支傳感器的時間t不變，因此同一傳感器不同周期測得的葉片振動位移值y也保持不變．葉尖定時測振系統對葉片同步振動的欠采樣模型如圖2 所示，同一傳感器采樣不同振動周期上的同一點．

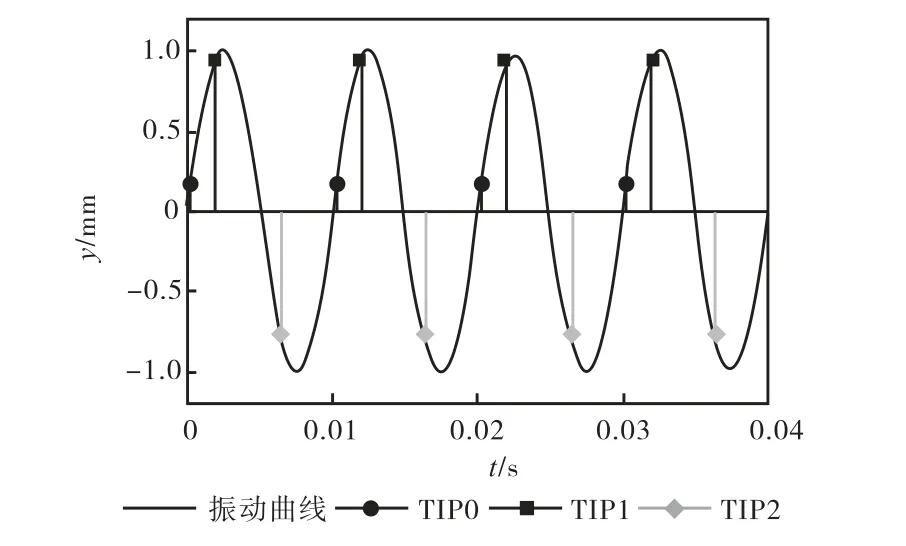
圖2 同步振動欠采樣Fig.2 Sub-Nyquist-sampling of synchronous vibration

由于葉片振動初始相位具有不定性以及振動倍頻未知，各傳感器獲取的恒定位移值具有不確定性，不能由單傳感器測得位移值判斷葉片是否存在同步振動．因此，直接由傳感器采樣的位移值獲取葉片同步振動信息比較困難．針對以上問題，設計一種辨識方法，利用各傳感器測得位移值的差異來辨識出同步振動參數，滿足葉尖定時測振系統在恒速對葉片振動測量要求．

2 多傳感器倍頻遍歷算法

在機殼上任意分布n(n≥4)支傳感器，按轉子旋轉方向傳感器依次編號為：0～n-1，相對0 號傳感器的安裝夾角分別為α0，α1，α2，…，αn-1(其中令α0＝0°)．由以上分析可知，葉片在恒速下發生同步振動時，不同的葉尖定時傳感器采樣到不同的恒定位移值

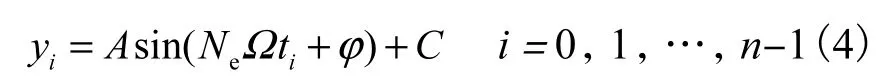
令葉片經過0 號傳感器的時刻定為t0＝0，忽略葉片本身振動帶來的時間誤差，葉片到達其他傳感器的時間為因此，各傳感器測得的振動位移值可表示為

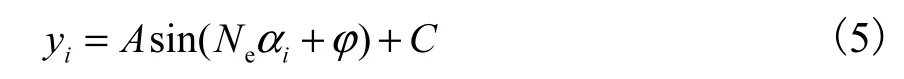
式(5)所示方程組包含n個方程，振動位移yi為測量值，A、Ne、φ和C都為未知數．方程組屬于超限定非線性方程組，其解不易直接求得．通過三角函數變換，式(5)可寫為

展開后寫成

分別令

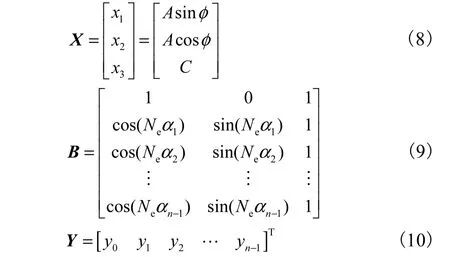
式(7)可寫成矩陣形式

將向量X看作未知向量，矩陣B看作系數矩陣，式(1)為超定線性方程組．由上述變換可知未知向量X中包含了A、φ和C 3 個未知數，而系數矩陣B中只包含了1 個未知數Ne．如果參數Ne已知，即可通過最小二乘法對其求解得到其他振動參數．而實際中，由于振動倍頻Ne值是一個自然數，并且旋轉機械主要葉片振動可能產生的倍頻值也是有限的，在旋轉機械設計時，已經基本估計出所有的主要振動倍頻范圍．選取一定的Ne范圍，對其進行遍歷，即將可能的Nek(k為自然數)值一一代入到式(11)中，通過最小二乘法求出對應的解向量

最小二乘解Xk代入式(11)與實際測得振動位移值Y的殘差定義為

以殘差Ek的標準差表示遍歷估計值偏離實際測量值的大小，即

考慮實際測量中的存在各種誤差，當遍歷倍頻Nek=時，Sk取最小值．因此倍頻遍歷過程中， 最小Sk值對應的倍頻Nek即為實際振動倍頻，從而求得解向量X *，計算葉片同步振動參數的公式如下．

振動頻率為

振動幅值為

振動相位為

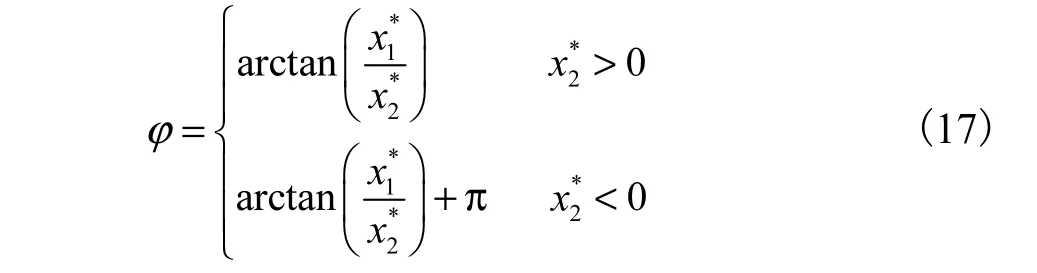
振動偏差為

由式(7)可知，未知的振動參數共4 個，因此振動倍頻遍歷方法要求利用4 支以上的葉尖定時傳感器．根據誤差理論，傳感器數量越多，獲取數據樣本越多，辨識精度也越高．但根據不同旋轉機械要求，實際傳感器安裝數量有限．傳感器的分布對該辨識方法有一定的影響，一般可任意分布．呈特殊規律分布的傳感器對特定倍頻值的振動將無法達到辨識效果．如“五均布”，傳感器安裝夾角α0～α4依次為：0°、72°、144°、216°、288°．對倍頻Ne進行遍歷時，角度N eαi需規整到一周內，即[0，360°）．當Ne為5的整數倍時(如Ne＝5，10，20，…)，規整后的N eα i均等于0°．因此式(7)等效一個等式，即等同于僅1支傳感器測量振動數據，而不能辨識出5 的整數倍振動倍頻的同步振動．為保證該方法的辨識效果，避免不同傳感器測量點的重復，采用無規律的任意分布可取得較好辨識效果．

3 實驗結果分析

為了驗證多傳感器倍頻遍歷方法對恒速下葉片同步振動的辨識效果，在某型號航空設備進行了模擬實驗驗證．實驗轉子及葉尖定時傳感器分布如圖3所示．轉子共8 個葉片，按圖3 所示逆時針旋轉．在葉片端部殼體上分布多支傳感器，順著轉速方向依次編號為TIP0～TIP6．安裝夾角α0～α6依次為：0°、18.4°、36.0°、53.6°、72.3°、119.5°、238.9°．實驗過程中，為了使葉片產生較明顯的同步振動，結合葉片設計先驗知識及葉片振動測試情況，選取葉片同步共振轉速(5,430,r/min、9,090,r/min、9,930,r/min 等)附近進行恒速實驗，并采用氮氣對葉片進行適當氣激．

圖3 同步振動測量實驗裝置Fig.3 Experimental facility of synchronous vibration measurement on rotating machinery

以9,090,r/min 附近恒速下測得的0 號葉片振動數據為例進行分析處理，截取實驗過程中1,000 圈數據，實測轉速平均值為9,089.2,r/min．傳感器測得的0 號葉片振動實時位移數據如圖4 所示．圖4(a)示出0 號傳感器測得的振動位移波形，其余傳感器測得波形類似．圖4(b)示出7 支傳感器測得0 號葉片振動位移平均值．每支傳感器同時采樣葉片的異步振動和同步振動，由前面分析可知，恒速下傳感器測得的同步振動位移值為一恒定值，因此各振動數據的平均值即可代表傳感器采樣的同步振動位移值．7 支傳感器測得0 號葉片的同步振動位移值y0～y6大小依次為 2.49 μm、－4.15 μm、40.52 μm、－22.84 μm、29.02 μm、－3.44 μm 和－6.04,μm．

圖4 恒速下葉片振動數據Fig.4 Blade vibration data at constant speed

根據多傳感器倍頻遍歷算法，結合先驗知識選取倍頻范圍1～30 進行遍歷．遍歷結果如圖5 所示，每個倍頻對應的Sk不同，可以明顯看到Ne＝12 時，出現最小值．因而確定葉片實際倍頻= 12，與理論分析一致．由式(15)～式(18)求得同步振動參數：f＝1,817.8,Hz ，A ＝0.033,mm ，φ＝－ 12.8 °，C ＝0.009,mm．已知葉片設計時的固有頻率在1,800,Hz附近，與辨識的振動頻率接近，可認為葉片在該轉速下發生同步共振．

利用以上辨識參數可以對該同步振動信號進行恢復，如圖6 所示，葉片每旋轉一周，7 支葉尖定時傳感器測得振動信號上7 點不同位移值．傳感器采集的位移值與恢復信號之間的標準差僅為2.3,μm，即信號恢復精度為2.3,μm．

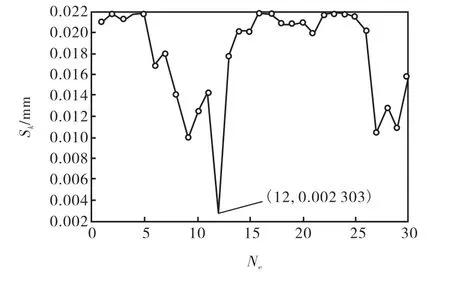
圖5 倍頻遍歷結果Fig.5 Results of traversing engine order

圖6 同步振動信號恢復Fig.6 Reconstruction of synchronous vibration signal

同理，按以上方法處理5,430,r/min 和9,930,r/min附近0 號葉片的振動數據，分別辨識出20 和11 倍頻的同步振動．3 個不同轉速辨識結果如表1 所示．

由表1 數據可以看到，不同轉速均能準確辨識出葉片同步振動，辨識結果與理論分析一致．另外，信號恢復精度隨振幅增大而變高，表明同步振動越明顯，辨識精度越高．

轉速/(r·min-1) 倍頻 振動頻率/Hz振幅/mm相位/(°)常偏量/mm信號恢復精度/μm 5,434.5 20 1811.5 0.018 65.1 0.008 3.03 9,089.2 12 1817.8 0.033 -12.8 0.009 2.30 9,928.8 11 1820.3 0.036 -59.6 0.013 1.06

4 結 語

本文基于葉尖定時測振原理，設計了一種恒速下旋轉葉片同步振動辨識方法并進行了模擬實驗驗證．利用多傳感器倍頻遍歷算法準確辨識出葉片同步振動參數，并且還原了同步振動信號，精度約2,μm，成功解決了恒速下葉尖定時測振對葉片同步振動欠采樣問題．該方法理論簡單，計算量小，易于實現，運用多傳感器測得位移值巧妙地達到振動辨識要求．主要應用于旋轉葉片恒速運行下的同步振動實時測量，結合葉尖定時測振中變速振動分析、異步振動分析等技術，形成一套完整的旋轉葉片振動實時監測系統，為旋轉機械安全運行提供可靠保障．

［1］Zielinski M，Ziller G，Non-contact vibration measurements on compressor rotor blades[J].Measurement Science and Technology，2000，11(7)：847-856.

［2］薩勃洛斯基. 渦輪機葉片振動的非接觸測量[M]. 吳士祥，鄭叔琛，譯. 北京：國防工業出社，1986：40-60.ЗАБЛОЦКИЙ И Е.Noncontact Measurement of Turbine Blades Vibration[M]. Wu Shixiang，Zheng Shuchen，trans. Beijing ： National Defence Industry Press ，1986：40-60(in Chinese).

［3］Gallego-Garrido J，Dimitriadis G. Validating synchronous blade vibration amplitudes from blade tip-timing data analysis[J].Institution of Mechanical Engineers，2004，623(23)：205-213.

［4］Bendali Salhi，Joseph Lardies，Marc Berthillier，et al.Modal parameter identification of mistuned blades disks using tip timing data[J].Journal of Sound and Vibration，2008，314(3/4/5)：885-906

［5］張玉貴，段發階，方志強，等. 間斷相位法測量葉片同步振動幅值的研究[J]. 振動與沖擊， 2008 ，27(10)：183-186.Zhang Yugui，Duan Fajie，Fang Zhiqiang，et al，Measuring synchronous vibration of rotating blades using discontinuous phase method[J].Journal of Vibration and Shock，2008，27(10)：183-186(in Chinese).

［6］張玉貴，段發階，方志強，等. 基于葉尖定時的非接觸式旋轉葉片異步振動分析[J]. 機械工程學報，2008，44(7)：147-150.Zhang Yugui ， Duan Fajie ， Fang Zhiqiang ， et al.Analysis of non-contact asynchronous vibration of rotating blades based on tip-timing[J].Chinese Journal of Mechanical Engineering，2008，44(7)：147-150(in Chinese).

［7］張玉貴，段發階，方志強，等. 速矢端跡法分析葉片同步振動幅值的方法研究[J]. 傳感技術學報，2007，20(9)：2044-2048.Zhang Yugui，Duan Fajie，Fang Zhiqiang，et al. Research on analyzing amplitude of synchronous blade vibration using speed-vector-end-track method[J].Chinese Journal of Sensors and Actuators，2007，20(9)：2044-2048(in Chinese)

［8］Heath S. A new technique for identifying synchronous resonances using tip-timing[J].Journal of Engineering for Gas Turbines and Power，2000，122(2)：219-225.

［9］Dimitriadis G，Carrington I B，Wright J R，et al.Blade-tip timing measurement of synchronous vibration of rotating bladed assemblies[J].Mechanical Systems and Signal Processing，2002，16(4)：599-622.

［10］Gallego-Garrido J，Dimitriadis G，Wright J R. A class of methods for the analysis of blade tip timing data from bladed assemblies undergoing simultaneous resonances[J].International Journal of Rotating Machinery，2007(1)：1-11.