顧先明

（唐山師范學院 數學與信息科學系，河北 唐山 063000）

第二型二元含參量正常積分函數的分析性質

顧先明

（唐山師范學院 數學與信息科學系，河北 唐山 063000）

根據含參量正常積分（積分限量函數的情形）的定義，類似地給出了第二型含參量正常積分函數的定義。研究發現第二型二元含參量正常積分函數在其定義域上具有連續性、可微性、可積性等分析性質，最后給出了一些應用實例。

含參變量正常積分函數；連續性；可微性；可積性

1 引理及預備知識

許多數學分析（或微積分學）教材都對含參變量正常積分做了較為細致的研究，均得到了含參量正常積分在其定義域上，當被積函數滿足一定條件后可以具有連續性、可微可積性等結果，但后繼的研究多集中在對已有結果的條件做改進或推廣，對含參量正常積分中被積函數推廣研究不多見。文[1]把含參量正常積分（積分限量為常數）的被積函數推廣到三元函數（甚至是n元函數）后，定義了一類二元含參量正常積分函數，并發現它在定義域上也具有連續性、可微性、可積性。本文將含參量正常積分（積分限量為常數）的被積函數推廣到三元函數，相應的積分限函數推廣到二元函數。然后定義了一類第二型二元含參量正常積分函數，進而探討該類函數的分析性質，并給出了一些實例。

定義1 一般地設f(x,y,z)為定義在區域

G ={(x, y, z) |α(x, y) ≤z ≤ β(x, y )(x, y) ∈ [a, b ]×[c, d ]}

上的三元函數，其中α (x ,y),β(x,y)為定義在矩形區域

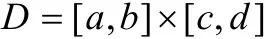
上的連續函數，若對于

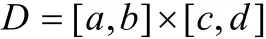
上有一固定點P( x, y)， f( x, y, z)作為z的函數在閉區間

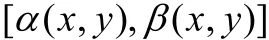
上可積，則其積分值是(x,y)在矩形區域

上取值函數，記作F(x,y)，則有

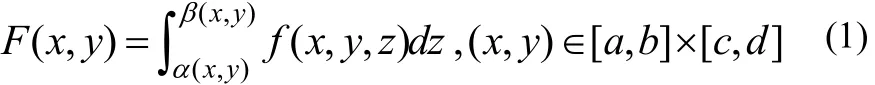
把形如⑴式的函數稱為第二型二元含參量正常積分函數（以下簡稱函數(1)）。

引理1 若 f( x,y,z)是定義在有界閉區間D上的連續函數，那么函數 f( x,y,z)在D上必可積。

引理 2 設函數f(x,y)的各偏導數在點( x0, y0)的某個鄰域上存在偏導數，在( x0, y0)點連續，那么f在點(x0,y0)處可微。

定理1 設函數f(x,y,z)為定義在區域

G ={(x, y, z) |α(x, y) ≤z ≤ β(x, y )(x, y) ∈ [a, b ]×[c, d ]}上的連續函數，其中α (x ,y),β(x,y)為矩形區域

2 主要結果及證明

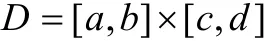
上的連續函數，則函數

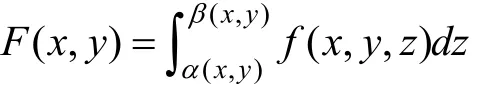
在區域

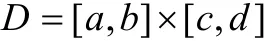
上連續。

證明 設P0( x0,y0)為 D= [a,b ]×[c,d ]

上任意一點，要證：

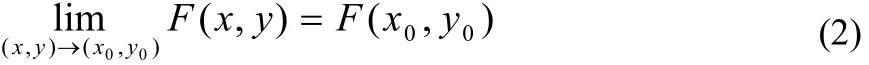
因為

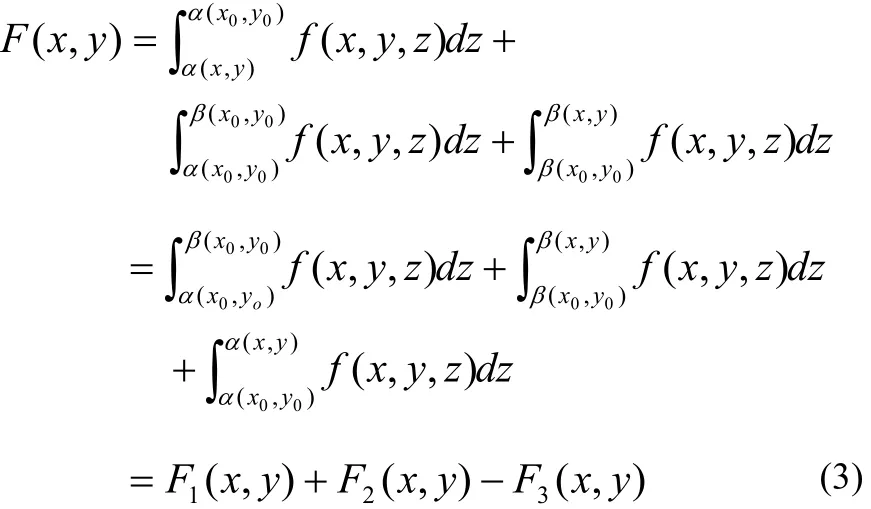
其中F1( x, y)，F2( x, y)，F3( x, y)分別為上式右端的三個積分。積分 F1(x,y)的積分限量是常數，滿足文[1]的條件，故

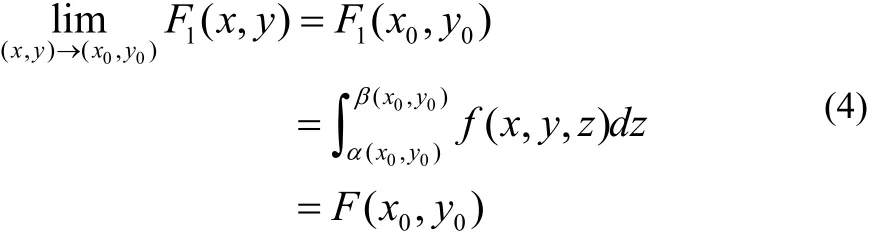
另外

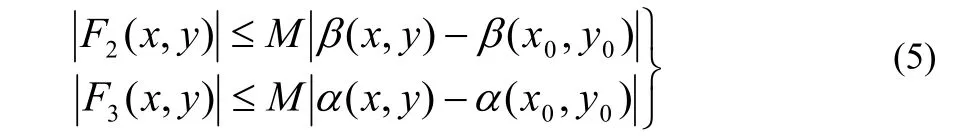
其中

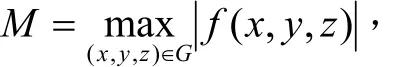
再根據 α(x ,y),β(x,y )的連續性，知(5)式右端趨于零，當(x, y)→ (x0,y0)時，從而

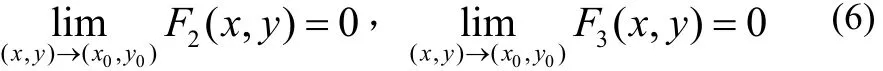
由(3)、(4)及(5)式即知(2)式正確。證畢。

定理2 設 f( x, y, z) , fx'( x, y, z) , fy'(x, y, z )都在長方體區域

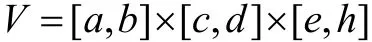
上連續，又設 α(x ,y),β(x,y)在矩形區域

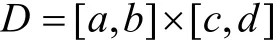
上具有連續偏導數，且滿足

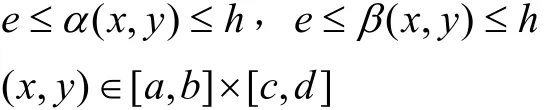
則函數

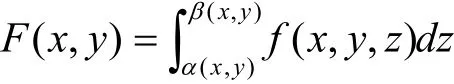
在D= [a,b ]× [c,d]上分別關于x,y可微，即

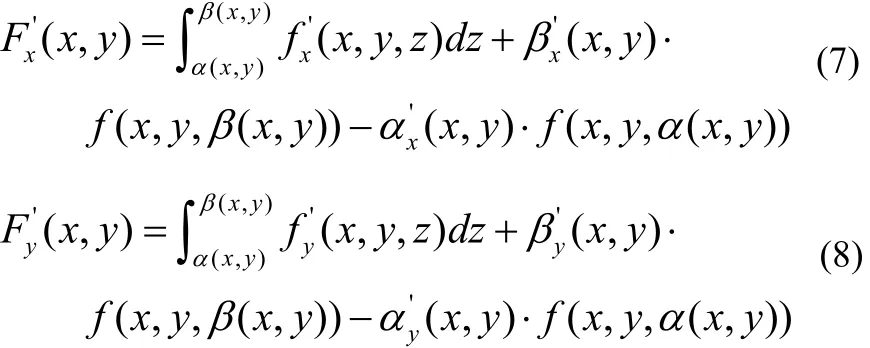
證明 這里只證(7)，(8)類似。

由于 F1(x,y)的積分限量是常數，滿足文[1]中定理3的條件，故有

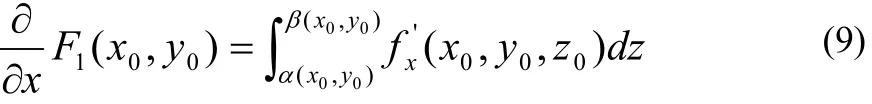
此外，由積分第一中值定理，可知

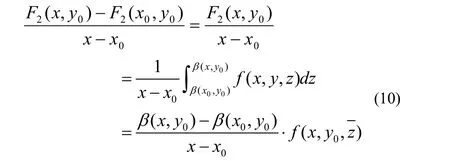
其中z在 β( x0, y0)與β( x,y0)之間，令(10)式中 x→ x0，并注意到此時→β(x0,y0)，即得

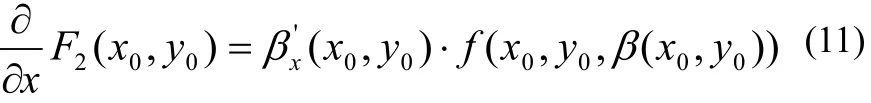
同理可證

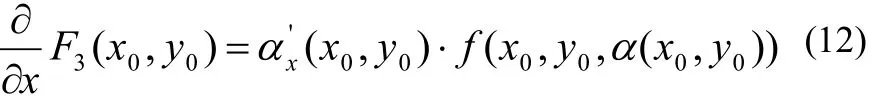
由(3)、(9)以及(11)、(12)，即知(7)當 (x,y)= ( x0, y0)時成立，由( x0, y0)可為矩形區域 D= [a,b] × [c,d ]中任一點，故知(7)對一切 (x, y)∈ [a,b]× [c,d]都成立。證畢。

推論1 若函數 f( x,y,z)滿足定理2的條件，則函數F (x,y)在矩形區域 D= [a,b ]× [c,d ]上可微。

證明 由定理2可知，F(x,y)的兩個偏導分別為

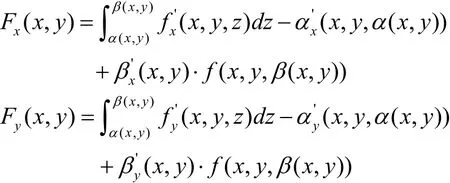
結合定理1，可知Fx(x,y)和Fy(x,y)的右端均是連續函數，即 Fx(x,y)和Fy(x,y)在定義域上存在且連續，再由引理1知，F(x,y)在矩形區域 D= [a,b] × [c,d ]上可微。

定理3 設函數 f( x,y,z)在區域

G ={(x, y, z) |α(x, y) ≤z ≤ β(x, y) (x, y) ∈[a, b ]×[c, d ]}上連續，其中α ( x, y) , β( x, y)為矩形區域

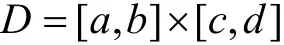
上連續函數，則函數

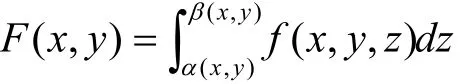
在區域 D= [a,b] × [c,d ]上可積。

證明 由定理1可知F(x,y)在 D= [a,b] × [c,d ]上連續，再結合[1]文引理1可知F(x,y)在D上可積。

從上述的證明過程可以看出，當將含參量正常積分（積分限量為函數）的被積函數推廣到三元以上函數，仍可以得到如前文所述的分析性質。

3 一些實例

例1 設

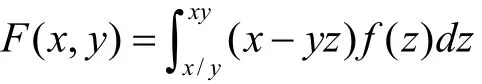
其中f(z)為可微函數，求 Fxy"(x, y)。

解 由已知條件并結合定理2知

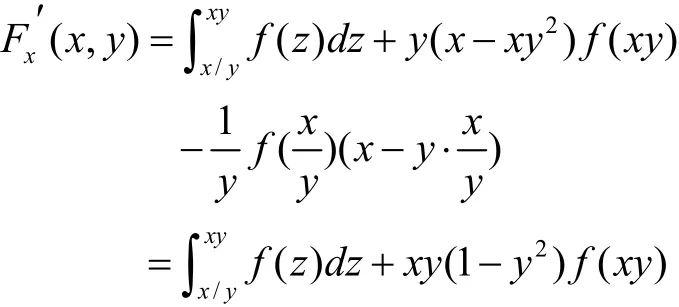
所以

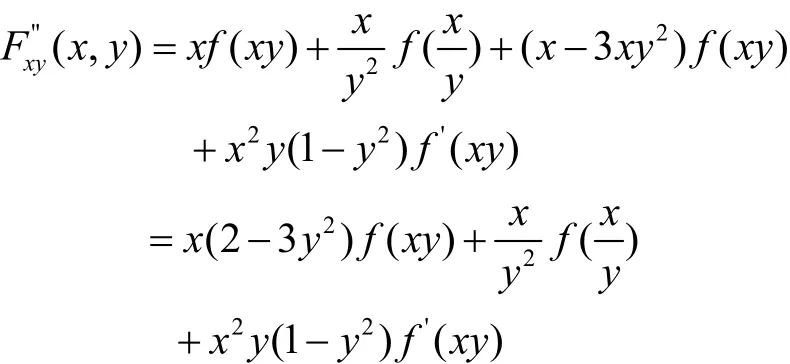
例2 設f(x)二階可微，F(x)可微，證明：

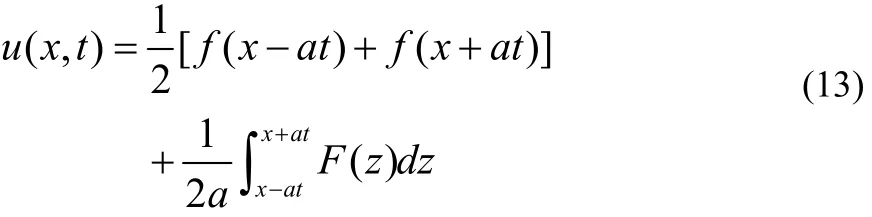
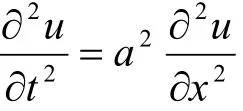
滿足弦振動方程及初值條件 u( x, 0) =f( x)， ut( x, 0) =F( x)。

證明 分別對x與t應用定理4

則由(14)和(15)知

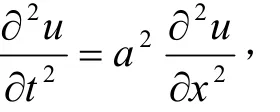
即u(x,t)是弦振動方程

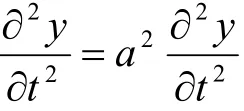
的解，且滿足

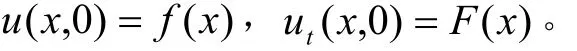
注 式(13)在偏微分方程中被稱為無限長弦自由振動達朗貝爾（d’ Alembere）公式或達朗貝爾（d’ Alembere）解。

[1] 顧先明.二元含參量正常積分函數的性質[J].唐山師范學院學報,2010,32(2)：41-44.

[2] 華東師范大學數學系.數學分析[M].北京：高等教育出版社,2006.

[3] 陳紀修等.數學分析[M].北京：高等教育出版社,2004.

[4] 常庚哲,史濟懷.數學分析教程[M].北京：高等教育出版社, 2003.

[5] 張筑生.數學分析新講[M].北京：北京出版社,2009.

（責任編輯、校對：趙光峰）

Analysis Characteristic of the Second Type of Normal Integral Function with Binary Parameter

GU Xian-ming

(Department of Mathematics and Information Science, Tangshan Teachers College, Tangshan 063000, China)

On the base of the definition of normal integral function (the case of integral limiter function), the definition and consequence of the second type with given parameters of normal integral function was carred out. It was found that, in its domain, this type of integral function was of continuity, differentiability and integrability. Some examples were given.

normal integral depending on a parameter; continuity; differentiability; integrability

唐山師范學院大學生科研立項項目

2010-04-25

顧先明（1989-），男，安徽壽縣人，唐山師范學院數學與信息科學系學生，研究方向為函數論。

O172

A

1009-9115(2011)05-0022-03