一道德國奧數題的巧解和錯解引發的探究

●

(南通高等師范學校 江蘇南通 226100)

一道德國奧數題的巧解和錯解引發的探究

●曹軍

(南通高等師范學校 江蘇南通 226100)

2008年德國數學奧林匹克有如下一道題目：

題目求最小的常數c，使得對所有的實數x，y，有

1+(x+y)2≤c(1+x2)(1+y2)．

《中等數學》2009年增刊第191頁給出如下巧解：

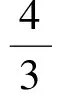
化簡整理得

(2x-y)2+(x-y)2≥0,

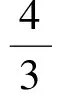
解法21+(x+y)2≤c(1+x2)(1+y2)等價于

cx2y2+(c-1)(x2+y2)-2xy+c-1.

(1)

令x=y=0，得c≥1，于是

cx2y2+(c-1)(x2+y2)-2xy+c-1≥

cx2y2+2(c-1)xy-2xy+c-1=

cx2y2+2(c-2)xy+c-1.

(2)

令xy=t，則t∈R，設f(t)=ct2+2(c-2)t+c-1.若f(t)≥0恒成立，則

(2c-4)2-4c(c-1)≤0，

解得

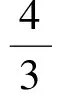
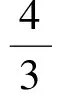
解法1的確太神秘了，就像從魔術師的帽子里突然鉆出兔子一樣，讓人匪夷所思.解法2雖比解法1自然，但遺憾的是解法有誤，于是筆者作了一番探究，現將探究過程整理出來，和大家分享．

g(x,y)=cx2y2+(c-1)(x2+y2)-2xy+c-1，

f(xy)=cx2y2+2(c-2)xy+c-1.

解法3(解法2的修正)

(1)當c≥2時，滿足題意.事實上,只需驗證

1+(x+y)2≤2(1+x2)(1+y2)，

化簡得

(x-y)2+2x2y2+1≥0，

這是顯然成立的.而

2(1+x2)(1+y2)≤c(1+x2)(1+y2)，

因此

1+(x+y)2≤c(1+x2)(1+y2).

(2)當c<2時，在原不等式中令x=y=0，得c≥1，于是

1≤c<2.

從而1+(x+y)2≤c(1+x2)(1+y2)等價于

cx2y2+(c-1)(x2+y2)-2xy+c-1≥0.

(3)

令g(x,y)=cx2y2+(c-1)(x2+y2)-2xy+c-1，則不等式(3)恒成立的充要條件是g(x,y)min≥0.

下面求g(x,y)min：由基本不等式x2+y2≥2xy,得

g(x,y)≥cx2y2+2(c-2)xy+c-1,

(4)

當且僅當x=y時，等號成立.記f(xy)=cx2y2+2(c-2)xy+c-1,令xy=t，則

f(xy)=f(t)=ct2+2(c-2)t+c-1(t∈R)，

因此

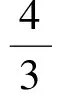
以上解法不但修正了解法2，而且揭開了解法1的神秘面紗，真可謂一舉兩得．其實，錯誤的解法都有某些合理的因素，充分挖掘并運用這些合理因素往往能修正錯誤的解法，甚至有時還能啟迪新的解題思路．進一步反思解法2，它是利用基本不等式放縮，轉化為一元二次不等式恒成立問題，利用判別式求解．然而已知的不等式本來既可以看作關于x的一元二次不等式，也可以看作關于y的一元二次不等式，因此利用基本不等式放縮顯得多余，由此引發了下面的創新解法.

解法4不等式1+(x+y)2≤c(1+x2)(1+y2)可化為

令x=y=0，得c≥1．對任意x,y∈R，式(6)恒成立等價于

Δ=4y2-4(cy2+c-1)(c-1)(y2-1)≤0

對任意y∈R恒成立，整理得

c(c-1)y4+c(2c-3)y2+(c-1)2≥0.

令y2=t，則等價于

c(c-1)t2+c(2c-3)t+(c-1)2≥0

對任意t∈[0,+∞)恒成立．

當c=1時，顯然不符合題意；

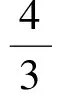
該賽題是一道含參數的恒成立問題，另一種常規思路是分離參數后轉化為最值問題，如果先分離參數，會怎樣呢？

解法5x,y∈R，1+(x+y)2≤c(1+x2)(1+y2)等價于對任意x，y∈R，有

(7)

即

(8)

(9)

注意到式(9)的分子、分母中3處出現了xy，結合分母中的x2+y2，自然想到用基本不等式x2+y2≥2xy來放縮，但必須考慮2xy-x2y2的正負．由式(9)可知，M的最大值在2xy-x2y2>0時取得，于是不妨設2xy-x2y2>0(即0

當且僅當x=y時，等號成立.

即

(2)配方法

解法3至解法5的共同特征都是先求出c的取值范圍，再確定c的最小值.解題過程比較繁瑣，有沒有簡捷的解法呢?自然會聯想到解法1.解法1雖神秘巧妙，令人匪夷所思，但它卻凸現了一個很重要的解題思想方法——先求必要性再驗證充分性，借鑒這種思想方法，將解法1稍作修改，可得解法6.

解法6由于式(7)對任意的實數x,y都成立，當然在特殊情形x=y下也成立，于是得到了式(7)的一個必要條件，即對任意x∈R，都有

即

接下來驗證充分條件，同解法1．

這道競賽題的探究歷程至少給我們如下2點啟示：第一，任何一種解法都有一定的價值，錯解也不例外，其價值有時并不在于錯誤本身，而在于從中可以挖掘合理因素，修正錯誤解法，化失敗為成功，甚至還能啟迪創新思路，因此教學中要注重錯誤資源的有效利用;第二，問題的巧解不是憑空產生的，它往往依托于通性解法，因此教學中既要注重教通法，又要注重教反思，通過引導學生對通法進行反思，使學生在反思中看到轉變思維的方向、方式、方法和策略，盡快獲得成功.這不僅使學生感到巧妙思路的到來是順其自然的，而且在發展學生思維、培養創新能力上無疑是一種很好的體驗和進步．

[1] 高孝君．一道德國數學奧林匹克試題的解答[J]．數學通訊(上半月)，2010(11-12)：117．