2011年全國高中數(shù)學(xué)聯(lián)賽模擬卷(一)
2011年全國高中數(shù)學(xué)聯(lián)賽模擬卷(一)
第一試
一、填空題
1.將數(shù)20分成5個(gè)實(shí)數(shù)之和,則這5個(gè)數(shù)的平方和的最小值是________.
2.設(shè)函數(shù)f(x)的定義域是N*,且f(x+y)=f(x)+f(y)+xy,f(1)=1,則f(2 011)=________.
3.設(shè)a,b,c,d為已知常數(shù),且b≥c≥d≥0,要使
|x-a|+|x-a+b|+|x-a+b-c|+|x-a+b+c|+|x-a+b-c+d|+|x-a+b+c-d|
為常數(shù),則x的取值范圍是________.
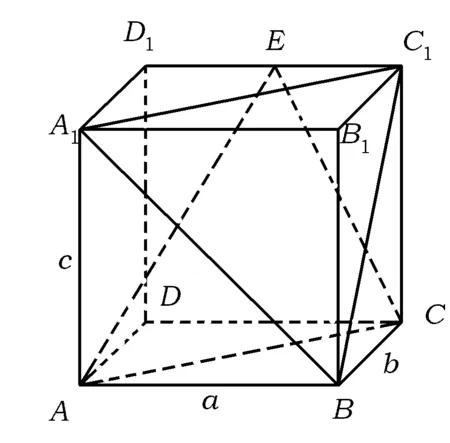
圖1
4.如圖1,長方體ABCD-A1B1C1D1,AB=a,BC=b,A1A=c,E為D1C1的中點(diǎn).若平面A1BC1與平面ACE所成二面角的平面角為θ,則sinθ=________.
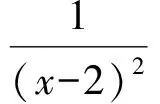
6.已知曲線y2=ax與其關(guān)于點(diǎn)(1,1)對稱的曲線有2個(gè)不同的公共點(diǎn),如果過這2個(gè)公共點(diǎn)的直線的傾斜角為45°,那么實(shí)數(shù)a=________.
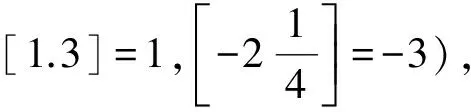
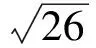
二、解答題

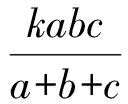
11.在數(shù)列{an}中,a1,a2是給定的非零整數(shù),an+2=|an+1-an|.證明:從{an}中一定可以選取無窮多項(xiàng)組成2個(gè)不同的常數(shù)數(shù)列.
第二試
一、在△ABC中,D,E,F(xiàn)和X,Y,Z分別為邊BC,CA,AB上的中點(diǎn)和高的垂足,ZD與FX交于點(diǎn)L,ZE與FY交于點(diǎn)M,DY與XE交于點(diǎn)N,求證:點(diǎn)L,M,N都在△ABC的歐拉線上(即三角形外心和垂心的連線上).
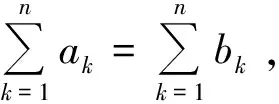
三、桌上放著個(gè)數(shù)分別為1,2,…,k的k堆石子(k≥3).第1步,任選3堆石子將它們合并成一堆,并在這堆石子中挑出一個(gè)石子扔掉;第2步,從現(xiàn)在桌上的所有石子堆中選出3堆石子將它們合并成一堆,并在這堆石子中挑出2個(gè)石子扔掉;…;一般地,第i步,在桌上選取石子總數(shù)大于i的3堆將它們合并成一堆,并在這堆石子中挑出i個(gè)石子扔掉.若經(jīng)過有限步上述操作后,桌面上僅剩下一堆p個(gè)石子.求證:當(dāng)且僅當(dāng)2k+2和3k+1都是完全平方數(shù)時(shí),p為完全平方數(shù),并求這樣的最小自然數(shù)k.
四、一副牌有2n+1張,其中有一張“王”,1,2,…,n各2張.把這2n+1張牌排成一行,使得王在中間,且對每個(gè)k(1≤k≤n),2個(gè)k之間恰有k-1張牌.當(dāng)n≤10時(shí),對怎樣的n,上述安排是可能的嗎?并給出相應(yīng)的安排方法.
參考答案
第一試
1.80 2.2 023 066 3.a(chǎn)-b≤x≤a-b+c-d
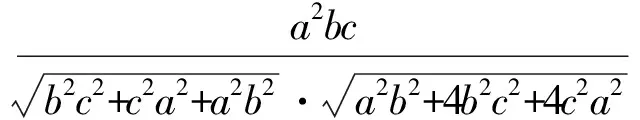
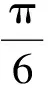
8.2n+1.
9.解存在符合條件的二次函數(shù).設(shè)f(x)=ax2+bx+c,則當(dāng)k=1,2,3時(shí),


聯(lián)立式(1),式(2),式(3),解得

于是

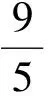


因此


10.解由均值不等式得
(a+b)2+(a+b+4c)2=
(a+b)2+[(a+2c)+(b+2c)]2≥
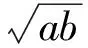
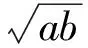
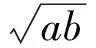
于是

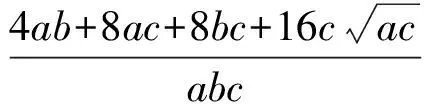
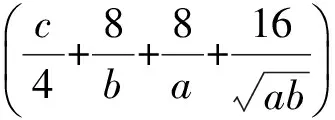
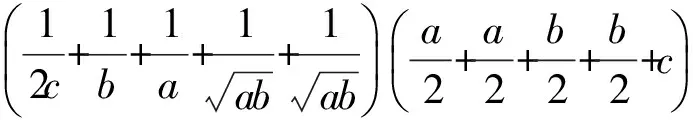
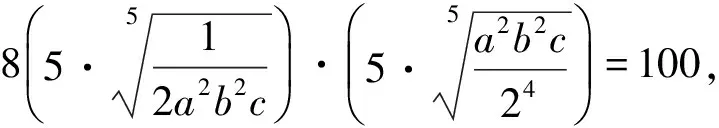
當(dāng)且僅當(dāng)a=b=2cgt;0,等號成立,故k的最大值為100.
11.解首先證明數(shù)列{an}必在有限項(xiàng)后出現(xiàn)零項(xiàng).假設(shè){an}中沒有零項(xiàng).由于
an+2=|an+1-an|,
因此當(dāng)n≥3時(shí),有an≥1.
當(dāng)an+1gt;an時(shí),
an+2=an+1-an≤an+1-1(n≥3);
當(dāng)an+1lt;an時(shí),
an+2=an-an+1≤an-1(n≥3),
即an+2的值要么比an+1至少小1,要么比an至少小1.令
則
0lt;bn+1≤bn-1.
由于b1是確定的正整數(shù),因此這樣下去,必然存在某項(xiàng)bklt;0,與bkgt;0矛盾,從而{an}中必有零項(xiàng).
若第一次出現(xiàn)的零項(xiàng)為an,記an-1=M(M≠0),則自第n項(xiàng)開始,每3個(gè)相鄰的項(xiàng)周期地取值0,M,M,即
因此數(shù)列{an}中一定可以選取無窮多項(xiàng)組成2個(gè)不同的常數(shù)數(shù)列.
第二試
一、證明設(shè)O,H分別為△ABC的外心和垂心,下面證明點(diǎn)L在OH上.設(shè)△ABC外接圓半徑為R.設(shè)直線ZC,F(xiàn)X交于點(diǎn)P,連結(jié)OF,HL,OL.由OF⊥AB,PZ⊥AB,得
OF∥PZ,
從而
∠OFL=∠P.
由F為Rt△AXB斜邊AB上的中點(diǎn),得FX=FB,從而
∠B=∠FXB=∠CXP,
于是
∠P=90°-∠ZFP=90°-2∠B.
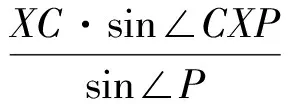
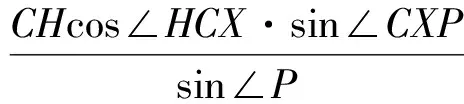
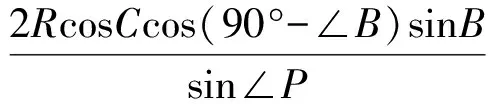
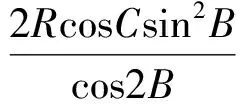
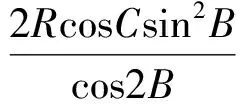
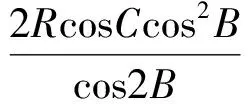
又由FO=RcosC,得
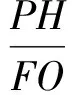
同理可得∠B=∠DZB.于是在△PLZ中,

在△FLZ中,
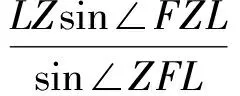
從而
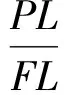
得
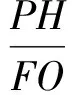
又因?yàn)椤螼FL=∠P,所以
△OFL∽△HPL,
而F,L,P共線,故O,L,H共線,即點(diǎn)L在OH上.
同理可證,點(diǎn)M,N也在OH上.
二、解不妨設(shè)12∈A,由于當(dāng)集合A確定后,集合B便唯一確定,因此只需考慮集合A的個(gè)數(shù),設(shè)A={a1,a2,…,a6},a6為最大數(shù).由1+2+…+12=78,得
a1+a2+…+a6=39,a6=12,
于是
a1+a2+a3+a4+a5=27,
故A1={a1,a2,a3,a4,a5}中有奇數(shù)個(gè)奇數(shù).
(1)若A1中有5個(gè)奇數(shù),因M中的6個(gè)奇數(shù)之和為36,而27=36-9,則A1={1,3,5,7,11},這時(shí)得到唯一的A={1,3,5,7,11,12}.
(2)若A1中有3個(gè)奇數(shù)、2個(gè)偶數(shù),用p表示A1中這2個(gè)偶數(shù)x1,x2之和;q表示A1中這3個(gè)奇數(shù)y1,y2,y3之和,則
p≥6,q≥9,
于是
q≤21,p≤18.
可得A1的24種情形.
1°當(dāng)p=6,q=21時(shí),
(x1,x2)=(2,4),
(y1,y2,y3)=(1,9,11),(3,7,11),(5,7,9),
可搭配成A1的3種情形;
2°當(dāng)p=8,q=19時(shí),
(x1,x2)=(2,6),
(y1,y2,y3)=(1,7,11),(3,5,11),(3,7,9),
可搭配成A1的3種情形;
3°當(dāng)p=10,q=17時(shí),
(x1,x2)=(2,8),(4,6),
(y1,y2,y3)=(1,5,11),(1,7,9),(3,5,9),
可搭配成A1的6種情形;
4°當(dāng)p=12,q=15時(shí),
(x1,x2)=(2,10),(4,8),
(y1,y2,y3)=(1,3,11),(1,5,9),(3,5,7),
可搭配成A1的6種情形;
5°當(dāng)p=14,q=13時(shí),
(x1,x2)=(4,10),(6,8),
(y1,y2,y3)=(1,39),(1,5,7),
可搭配成A1的4種情形;
6°當(dāng)p=16,q=11時(shí),
(x1,x2)=(6,10),(y1,y2,y3)=(1,3,7),
可搭配成A1的1種情形;
7°當(dāng)p=18,q=9時(shí),
(x1,x2)=(8,10),(y1,y2,y3)=(1,3,5),
可搭配成A1的1種情形.
(3)若A1中有1個(gè)奇數(shù)、4個(gè)偶數(shù),由于M中除12外,其余的5個(gè)偶數(shù)和2+4+6+8+10=30,從中去掉一個(gè)偶數(shù),補(bǔ)加一個(gè)奇數(shù),使A1中五數(shù)之和為27,分別得到A1的4種情形:(7,2,4,6,8),(5,2,4,6,10),(3,2,4,8,10),(1,2,6,8,10).
綜合以上討論,可知集合A有1+24+4=29種情形,即M有29種“等和劃分”.
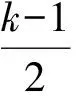
下面分k≡1(mod 4)和k≡3(mod 4)這2種情況來解決問題.
(1)若k≡1(mod 4),記k=4c+1,則開始時(shí)共有石子

經(jīng)過2c步共扔掉的石子數(shù)為
1+2+…+2c=c(2c+1),
故p=(4c+1)(2c+1)-c(2c+1)=
(2c+1)(3c+1).
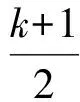
(2)若k≡3(mod 4),記k=4c+3,則
3k+1=12c+10≡2(mod 4),
不可能為完全平方數(shù).
下證p也一定不是完全平方數(shù).此時(shí)總的石子數(shù)為
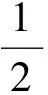
2(4c+1)(c+1).
經(jīng)過2c步共扔掉的石子數(shù)為
1+2+…+2c=(c+1)(2c+1),
故p=2(4c+1)(c+1)-(c+1)(2c+1)=
(c+1)(6c+5).
若p為完全平方數(shù),則由(c+1,6c+5)=1知,c+1和6c+5均為完全平方數(shù).記c+1=x2,6c+5=y2,則6x2-y2=1,y為奇數(shù),于是
y2≡1(mod)8,6x2≡2(mod 8).
故3x2≡1(mod 4),這不可能,故p不為完全平方數(shù).
綜上所述,當(dāng)且僅當(dāng)2k+2和3k+1都是完全平方數(shù)時(shí),p為完全平方數(shù).
下面尋找滿足條件的最小自然數(shù)k.由上面的證明可得k=4c+1(c≥1),因此只需尋找最小的c.記2c+1=x2,3c+1=y2,則
顯然x≡1(mod 2),x2≡1(mod 4),則
2y2=2(mod 4),y≡1(mod 2).
設(shè)x=2a+1,y=2b+1,則式(4)變?yōu)?/p>
3a(a+1)=2b(b+1)。
將a=1,2,…逐一代入,知最小的a=4,此時(shí)b=5,故最小的
k=4c+1=2x2-1=2(2a+1)2-1=161.
四、解把2n+1個(gè)位置從左到右依次記為第1號位,第2號位,…,第2n+1號位.
對每個(gè)k(1≤k≤n),設(shè)左邊的那個(gè)k位于第ak號位,右邊的k位于第bk號位.由于2個(gè)k之間恰有k-1張牌,因此k=ak+k,即
(ak+bk)-2ak=k.
對k從1到n求和,得
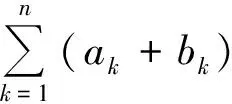
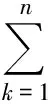
2n(n+1).
由式(5),得
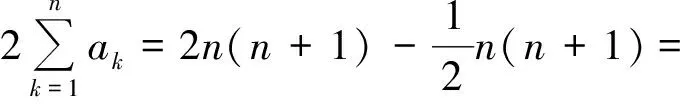
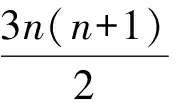
當(dāng)n=3,4,7,8時(shí),滿足題設(shè)要求的安排是可能的,具體排法如下:
當(dāng)n=3時(shí),1 1 3 王 2 3 2;
當(dāng)n=4時(shí),1 1 3 4 王 3 2 4 2;
當(dāng)n=7時(shí),1 1 3 6 7 3 4 王 5 6 4 7 2 5 2;
當(dāng)n=8時(shí),5 8 4 1 1 5 4 7 王 8 6 2 3 2 7 3 6.
(供稿人:虞金龍)

