2011年希望杯全國數學邀請賽初三競賽二試模擬卷(二)

2011年希望杯全國數學邀請賽初三競賽二試模擬卷(二)

一、選擇題(共8小題，每小題5分，滿分40分)

1．直四棱柱、長方體和正方體之間的包含關系是

( )

A. B. C. D.

2．由多項式乘法m(a+b+c)=ma+mb+mc，可得：(a+b)(a2-ab+b2)=a3+b3,我們把上述等式叫做多項式乘法的立方公式.下列應用這個立方公式進行的變形不正確的是

( )

A．(x+4y)(x2-4xy+16y2)=x3+64y3B．(2x+y)(4x2-2xy+y2)=8x3+y3

C．(a+1)(a2+a+1)=a3+1 D．x3+27=(x+3)(x2-3x+9)

( )

圖1

4．小毛和大毛各有一副三角尺和一個量角器(如圖1),他們分別從自己這3件文具中隨機取出1件,則可以拼成一個軸對稱圖案的概率是

( )

5．拋物線y=ax2+bx+c關于x軸對稱的二次函數解析式是

( )

A．y=-ax2-bx-cB．y=-ax2+bx-c

C．y=ax2-bx+cD．y=ax2-bx-c

( )

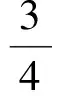
圖2

7．如圖2，點P是⊙O的弦AB上的一點，連結OP，過點P作PC⊥OP，PC交⊙O于點C，若BP=4,CP=8，則AP的長為

( )

A.10B.12C.14D.16

8．為提高信息在傳輸中的抗干擾能力，通常在原信息中按照一定規則加入相關數據組成傳輸信息．設定原信息為a0a1a2,ai∈{0,1}(i=0,1,2)，傳輸信息為h0a0a1a2h1，其中h0=a0?a1,h1=h0?a2，?運算規則為：0?0=0，0?1=1，1?0=1，1?1=0，例如原信息為111，則傳輸信息為01111．傳輸信息在傳輸過程中受到干擾可能導致接收信息出錯，則下列接收信息一定有誤的是

( )

A.11010 B.01100 C.10111 D.00011

二、填空題(共8小題，每小題5分，滿分40分)

9.如圖3所示的圖形是某些多面體的平面展開圖,請寫出它們的名稱:

①____________;②____________;③____________;④____________.

圖3

10．若0≤x≤1,且x2+y2=3，xy=1，則x-y=________.

11．在△ABC中,AB=AC,邊AC上的中線BD把△ABC的周長分成12和18兩部分，則△ABC各邊的長為________.

12．有A,B,C三粒骰子，骰子A的6個面上分別刻有1,2,3,4,5,6；骰子B的6個面上分別刻有1,3,5,7,9,11；骰子C的6個面上分別刻有2,4,6,8,10,12.現將它們拋擲后，面朝上的3粒骰子上的點數和為12的概率是________.

圖4 圖5

14.如圖4，⊙O與Rt△AOB的斜邊交于點C,D,C,D恰是AB的2個三等分點.若⊙O半徑的長等于5,則AB=________.

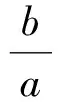
圖6

16．如圖6，n+1個邊長為2的等邊三角形有一條邊在同一直線上，設△B2D1C1的面積為S1，△B3D2C2的面積為S2，…，△Bn+1DnCn的面積為Sn,則S2=________；Sn=________(用含n的式子表示)．

三、解答題(共2小題，每小題20分，滿分40分)

17．在等腰梯形ABCD中，CD∥AB，對角線AC,BD相交于點O,∠ACD=60°,點P,Q,S分別為OA,BC,OD的中點．

(1)求證：△PQS是等邊三角形;

(2)若AB=5，CD=3,求△PQS的面積；

(3)若△PQS的面積與△AOD的面積比是7∶8，求梯形上、下底的比CD∶AB．

18．已知拋物線y=ax2+bx+c(a≠0)的對稱軸為x=1,與x軸交于點A,B,與y軸交于點C,其中B(3,0),C(0,2).

(1)求這條拋物線的解析式.

(2)已知在對稱軸上存在一點P,使得△PAC的周長最小(可不必證明),請求出點P的坐標.

(3)若點D是線段OC上的一個動點(不與點O、點C重合),過點D作DE∥PC交x軸于點E,連結PD,PE.設CD的長為t,△PDE的面積為S,求S與t之間的函數關系式,試說明S是否存在最大值.若存在,請求出這個最大值;若不存在,請說明理由.

參考答案

1．A 2．C 3．D 4．B 5．A 6．B 7．D 8．C

9.①長方體;②三棱柱;③三棱錐;④圓錐

圖7

17．(1)證明如圖7，連結PB，SC,容易證明△DAB≌△CBA，則

∠OAB=∠OBA.

又由∠ACD=60°，可知△COD,△AOB都是等邊三角形.由PB⊥OA,得

同理可得

于是

(3)解設CD=a,AB=b(bgt;a),則

S△AOD∶S△COD=b∶a，

從而

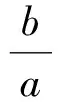
又由S△SPQ∶S△AOD=7∶8，得

8S△SPQ=7S△AOD，

即

于是

2a2-5ab+2b2=0，

解得

b=2a，

從而

CD∶AB=1∶2．

圖9

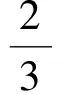
(2)連結BC,交對稱軸x=1于點P,可知△PBC的周長最小.根據點B,C的坐標可得過點B,C的直線的一次函數解析式為

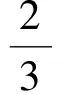
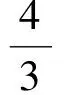
(3)由△OED∽△OBC，得

即

得

連結OP,得

S=S四形邊PDOE-S△OED=

S△POE+S△POD-S△OED=

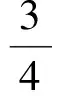
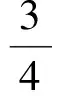
(供稿人：施 儲)