簡談二次函數的綜合應用

●

(蘇步青學校 浙江平陽 325404)

簡談二次函數的綜合應用

●周增強

(蘇步青學校 浙江平陽 325404)

二次函數是初中數學教學的重要內容之一．作為最基本的初等函數，二次函數內容廣泛，頗受命題者青睞．各地中考試題中二次函數的考題，既有解析式、值域與最值等基本內容，也有通過與二次方程、二次不等式的聯系而變化出各種各樣的代數問題；還有大量的從圖像角度、結合坐標系衍生而成的數形結合問題.這類問題綜合性強、難度大，往往以壓軸題的形式出現.本文將通過一些中考試題和模擬題對二次函數綜合應用進行分類說明.

1 實際應用題

例1利達經銷店為某工廠代銷一種建筑材料(這里的代銷是指廠家先免費提供貨源，待貨物售出后再進行結算，未售出的由廠家負責處理)．當每噸售價為260元時，月銷售量為45噸.該經銷店為提高經營利潤，準備采取降價的方式進行促銷.經市場調查發現：當每噸售價下降10元時，月銷售量就會增加7.5噸．綜合考慮各種因素，每售出1噸建筑材料共需支付廠家及其他費用100元.設每噸材料售價為x(元)，該經銷店的月利潤為y(元).

(1)當每噸售價為240元時，計算此時的月銷售量；

(2)求出y與x的函數關系式(不要求寫出x的取值范圍)；

(3)該經銷店要獲得最大月利潤，售價應定為每噸多少元？

(4)小靜說：“當月利潤最大時，月銷售額也最大”,你認為對嗎？請說明理由.

解(1)由題意得，月銷售量為

45+(260-240)×7.5÷10=60(噸).

(2)根據題意得

即

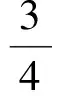
(3)對第(2)小題的結論配方得

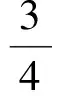
因此利達經銷店要獲得最大月利潤，材料的售價應定價為每噸210元.

(4)小靜說的不對.當月利潤最大時，x為210元，此時月銷售額為17 325元；當x為200元時，月銷售額為18 000元.因為

17 325lt;18 000，

所以當月利潤最大時，月銷售額不是最大，故小靜說的不對.

說明這是二次函數的性質在實際問題中的應用.解這類題型的重點是列出二次函數的關系式，然后運用二次函數的性質解題.

2 動點運動問題

圖1

(1)求這條拋物線的函數關系式.

(2)2個動點P，Q分別從點O，A同時出發,以每秒1個單位長度的速度運動.其中點P沿著線段OA向點A運動，點Q沿著折線A→B→C的路線向點C運動.設這2個動點運動的時間為t(秒)(0lt;tlt;4)，△PQA的面積記為S.

①求S與t的函數關系式.

②當t為何值時，S有最大值，最大值是多少？并指出此時△PQA的形狀.

③是否存在這樣的t值，使得△PQA是直角三角形?若存在，請直接寫出此時點P,Q的坐標；若不存在，請說明理由.

解得

故所求拋物線的函數關系式為

(2)①過點B作BE⊥x軸于點E，則

∠BAE=60°.

1°當點Q在線段AB上運動，即0lt;t≤2時，

QA=t，PA=4-t.

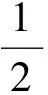
綜合1°，2°可得

②1°當0lt;t≤2時，

2°當2≤tlt;4時，

③存在.當點Q在線段AB上運動時，要使得△PQA是直角三角形，必須使得∠PQA=90°，這時PA=2QA，即

4-t=2t，

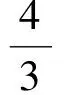
說明該動點問題的解題思路是先利用二次函數描述動點的運動規律，然后再具體運算求解.

3 含參數問題

例3已知y2=4a(x-a)(agt;0)，且當x≥a時，S=(x-3)2+y2的最小值為4，求參數a的值．

解將y2=4a(x-a)代入S的表達式中，得

S=(x-3)2+4a(x-a)=

x2-2(3-2a)x+9-4a2=

[x-(3-2a)]2+12a-8a2,

則S是關于x的二次函數，其定義域為xgt;a，對稱軸方程為x=3-2a，頂點坐標為(3-2a,12a-8a2)，圖像開口向上．

若3-2a≥a，即0lt;a≤1,則當x=3-2a時，

S最小=12a-8a2=4,

此時

若3-2alt;a，即agt;1,則當x=a時，

S最小=[a-(3-2a)]2+12a-8a2=4,

此時

a=5或a=1(因agt;1,故a=1舍去).

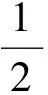
說明函數中的參數問題一般是先對參數范圍進行分析，再結合函數性質獲得等量關系進行求解．

4 圖形信息題

例4某公司推出了一種高效環保型除草劑，年初上市后，公司經歷了從虧損到盈利的過程.圖2的二次函數圖形(部分)表示了該公司年初以來累積利潤S(萬元)與時間t(月)之間的關系(即前t個月的利潤總和S與t之間的關系).

根據圖形提供信息，解答下列問題：

(1)公司從第幾個月末開始扭虧為盈；

(2)累積利潤S與時間t之間的函數關系式；

(3)求截止到何月末公司累積利潤可達30萬元；

(4)求第8個月公司所獲利是多少元？

圖2

解(1)由圖2可知公司從第4個月末以后開始扭虧為盈.

(2)由圖2可知頂點坐標為(2,-2)，可設其函數關系式為

y=a(t-2)2-2.

因為所求函數關系式的圖形過點(0,0)，所以

a(t-2)2-2=0,

解得

從而所求函數關系式為

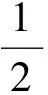
即

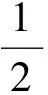
t1=10，t2=-6(舍去),

因此截止到10月末公司累積利潤可達30萬元.

(4)把t=7代入關系式，得

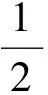
把t=8代入關系式，得

因為

16-10.5=5.5.

所以第8個月公司所獲利是5.5萬元.

說明圖形信息題顧名思義是指圖形中蘊含著條件信息，一般通過圖形中已知的點坐標，根據合適的二次函數表達式列出二次函數，從而使問題獲解．

5 代數推理題

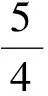
證明因為f(-1)=a-b+c,

f(1)=a+b+c,f(0)=c,

所以

當-1≤x≤0時，

-x2-x+1=

當0≤x≤-1時，

-x2+x+1=

綜上所述，問題獲證.

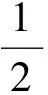
6 探索性問題

圖3

(1)求點D的坐標.

(2)求經過點O，B，D的拋物線解析式.

(3)判斷在第(2)小題中所得的拋物線上是否存在一點P，使得ΔDCP∽ΔOCD？若存在，求出點P的坐標；若不存在，請說明理由．

解(1)連結AD，則AD⊥CD于點D,作DE⊥OA于點E．由點A的坐標為(1，0)，且OC=2OA，可得AC=3，因此

于是

解得

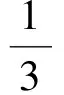
因而

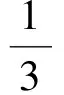
得

解得

故所求拋物線的解析式為

(3)設⊙A與x軸的另一個交點為F(2,0)，連結DF. 由CD切⊙A于點D，得

∠CDO=∠CFD.

又∠DCO=∠FCD，因此

△OCD∽△DCF.

說明二次函數探索性問題的解法并不唯一，重點是找到條件間的關系，對每一個已知條件進行分析利用．在探索性問題中比較常見的是存在性問題，這類問題的一般解法有2種，一是假設結論存在，若求出的結論符合已知條件，則結論存在；若求出結論不符合已知條件或與定理、公理等相矛盾，則結論不存在．二是像本題這樣，先找到特殊點(或特殊值)等，然后證明這些點或值就是解決問題所需要的.

[1] 梁麗平，安振平.二次函數綜合問題例談[J].數理化學習(高中版),2006(1):2-6.

[2] 顧國璽.二次函數知識的綜合應用[J].數理化解題研究(初中版),2011(2):18-20.