關于“點共圓”問題的普及

●

(鎮海蛟川書院 浙江寧波 315200)

關于“點共圓”問題的普及

●劉清泉

(鎮海蛟川書院 浙江寧波 315200)

“點共圓”是數學競賽中的一項重要內容，三角形、四邊形中的很多內容都與之關聯.但隨著新課程改革對邏輯推理要求的降低，特別是初中教材中對“點共圓”涉及的不多，在數學競賽中與“圓”相關內容的比例也在降低.此時,與“點共圓”的相關內容和相關方法更顯得重要.本文力求用幾個平面幾何中相關的定理知識將這一內容作一有機的整合.

1 基礎知識

如圖1～3，A，B，C，D四點共圓，得到如下3個結論:

(1)∠A=∠D；

(2)∠A+∠C=180°；

(3)∠PAD=∠C.

分別概括為：①同弦同側張角相等；②同弦異側張角互補；③外角等于內對角.

圖1 圖2 圖3

在圖1和圖3中,分別可得：

(4)PA·PC=PB·PD；

(5)PA·PB=PC·PD.

即“圓冪定理”中的“相交弦定理”(記為④)和“割線定理”(記為⑤).同時，不難證明：定理①～⑤的逆命題也是真命題.原命題是“四點共圓”的性質，其逆命題可作為“四點共圓”的判定.另外，一些特殊的四邊形，如矩形、等腰梯形、一組對角都為直角的四邊形是圓內接四邊形，常常作為解題,特別是添加輔助線的切入點.

2 知識應用

2.1 費馬點(三角形每個內角都小于120°的費馬點)

例1△ABC的每個內角都小于120°，在△ABC的內部找一點P，使得PA+PB+PC最小.

分析為求線段和的最小值，先將“丫”字形的3條線段PA，PB，PC,通過旋轉變換轉化為一條折線段.

解如圖4，將△APB繞點B逆時針旋轉60°得到△A′P′B.連結PP′，易證△PBP′為正三角形，從而

PB=P′P.

又由PA=P′A′，得

PA+PB+PC=A′P′+P′P+PC,

即對于△ABC內的任意一點P，PA，PB，PC的長度之和等于2端A′，C固定的折線A′P′PC的長，當且僅當A′，P′，P，C共線時，其值最小.此時由

∠A′P′B+∠BP′P=∠BPP′+∠BPC=180°

及

∠BP′P=∠BPP′=60°，

得

∠A′P′B=∠BPC=120°，

從而

∠APB=∠BPC=∠CPA=120°.

此時點P稱為△ABC的“費馬點”(又稱“正等角中心”).

圖4 圖5 圖6

怎樣用直尺、圓規來確定這個點呢？

如圖5，以△ABC的邊BC，CA為邊向外作正三角形△BCA′，△CAB′.連結AA′，BB′交于點P，易證△ACA′≌△B′CB，因此

∠A′AC=∠BB′C，

得A，B′，C，P四點共圓，從而

∠A′PC=∠AB′C=60°，

∠BPA′=∠APB′=∠ACB′=60°，

得

∠BPC=120°.

同時由∠CPA+∠AB′C=180°,得

∠CPA=120°，

于是

∠APB=∠BPC=∠CPA=120°，

故AA′，BB′的交點即為“費馬點”.

更進一步探究，此時再以AB為一邊向外作正三角形△ABC′，連結AA′，BB′，CC′,這3條線共點嗎？

如圖6，將AA′，BB′，CC′三線共點轉化為點C，C′及AA′與BB′確定的交點P三點共線.連結CP，C′P.由∠APB+∠AC′B=180°，得A，P，B，C′四點共圓，從而

∠C′PB=∠C′AB=60°.

進而由∠C′PB+∠BPC=180°，得C，P，C′三點共線，證畢.

對于論證三角形每個內角都小于120°的費馬點的其他方法,以及三角形有一個內角不小于120°的費馬點退化為120°的內角頂點問題,在此不再贅述.

2.2 托勒密定理與逆定理

2.2.1 托勒密不等式

例2對于四邊形ABCD，恒有

AB·CD+BC·DA≥AC·BD.

簡證如圖7，在四邊形內取點E，使得

∠1=∠2，∠3=∠4，

得

△ABE∽△ACD，

從而

即

AB·CD=BE·AC.

∠BAC=∠EAD，

因此

△ABC∽△AED，

從而

得

BC·DA=DE·AC，

于是

AB·CD+BC·DA=BE·AC+DE·AC=

(BE+DE)·AC≥

BD·AC.

進一步，當且僅當B，E，D共線時等號成立，此時圖中∠5=∠1.又∠1=∠2，得∠5=∠2，即A，B，C，D四點共圓.由此不難得到：在圓內接四邊形ABCD中，有

AB·CD+BC·DA=AC·BD(托勒密定理)；

對于四邊形ABCD，若AB·CD+BC·DA=AC·BD，則這個四邊形內接于一圓(托勒密定理的逆定理).

圖7 圖8

2.2.2 用托勒密不等式證明費馬點

例3△ABC的每個內角都小于120°，在△ABC的內部找一點P，使得PA+PB+PC最小.

簡證設點P為△ABC的正等角中心(即費馬點)，如圖8,作出△BPC的外接圓，并設AP交該圓于點P′.由△P′BC為圓的內接三角形，可證

PP′=PB+PC，

因此

PA+PB+PC=AP′.

設Q為不同于點P的任意一點，由托勒密不等式得

QC·BP′+QB·CP′≥BC·P′Q，

即

QC+QB≥P′Q，

故

QC+QB+QA≥P′Q+QA≥AP′=

PA+PB+PC，

當且僅當Q為圓與AP′在三角形內的交點，即點Q與點P重合時,取到等號.

2.3 九點圓

例4點O1，O2，O3分別為△ABC中邊BC，CA，AB的中點，點H為△ABC的垂心，點H1，H2，H3分別為高足，點D1，D2，D3分別為AH，BH，CH的中點.求證：點O1，O2，O3，H1，H2，H3，D1，D2，D3九點共圓.

分析欲證多點共圓，常用的辦法有:

(1)圓的定義：到定點距離等于定長；

(2)先證四點共圓，再證其余的點在這個圓上；

(3)先分別證明幾組點共圓，再證明這幾個圓重合.

圖9

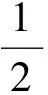
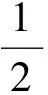
2.4 蝴蝶定理

(1)蝴蝶定理及常見證明方法.

例5在⊙O中，弦CD，EF過弦AB中點M，弦CF，DE分別交AB于點P，Q.求證：PM=QM.

方法1“軸對稱”法

分析如圖10，作直線OM(⊙O的對稱軸)，以OM為對稱軸作C的對稱點C′，則點C′在圓上.連結C′Q，可證△PMC≌△QMC′.又已知∠1=∠2，MC=MC′，可證∠3=∠4.由圓周角定理得∠3=∠5，即證∠4=∠5，故而轉化為C′，M，Q，E四點共圓的證明.

圖10 圖11

途徑1如圖11，連結CC′，C′E，易知CC′∥PQ，不難得到∠2=∠8=∠7.由C，D，E，C′四點共圓，得

∠6+∠7=180°，

從而

∠6+∠2=180°.

途徑2如圖12，連結C′E，延長C′M交⊙O于點D′，連結BD′，可得

∠2+∠6=180°.

注：以上2條途徑以“同線異側張角互補”作為落點得以證明，當然也可以把“同線同側張角相等”(如圓周角∠EC′Q與圓內角∠EMQ相等)作為落點得以證明.

圖12 圖13

方法2“相似”法

分析把一組對角都為直角的四邊形是圓內接四邊形作為添加輔助線的切入點.

簡證如圖13，作OG⊥FC于點G，作OH⊥DE于點H.由垂徑定理得

連結OM,OP,OQ,MG,MH,易知

△FMC∽△DME，

得

因此

又∠F=∠D,得△FMG∽△DMH，故∠1=∠4.

由垂徑定理知OM⊥AB，又OG⊥FC，OH⊥FC，得O，G，P，M四點共圓，O，H，P，M四點共圓，從而

∠1=∠2，∠3=∠4，

即∠2=∠3，結合OM⊥PQ易證結論.

注：蝴蝶定理的證法很多，但在初中范圍內這2種證法最易于接受.

(2)蝴蝶定理的推廣.

圖14 圖15

圖16 圖17

2.5 海倫公式的推廣

證明2S=ad·sin∠BAD+bc·sin∠BCD=

(ad+bc)·sin∠BAD.

由

BD2=a2+d2-2adcos∠BAD=

b2+c2-2bccos∠BCD=

b2+c2+2bc·cos∠BAD,

得

則

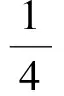
即

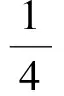
于是

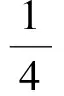
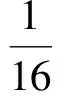
bc)-(a2+d2-b2-c2)]=

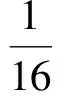
(b+c+d-a),

故

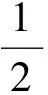
從以上內容可以看出，“點共圓”在平面幾何

圖18

中廣泛存在且至關重要，平面幾何中的很多重要定理都與之相關，再譬如：(1)“法尼阿諾——許瓦茲問題”(在銳角△ABC的3邊各取一個點M,N,P，使△MNP的周長最短)中的光路三角形與高足三角形；(2)“米庫勒定理”(如圖18，延長凸五邊形ABCDE各邊得一五角星，它的5個三角形分別是△ABF，△BCG，△CDH，△DEI，△EAJ，它們的外接圓兩兩相交得到的不同于五邊形ABCDE頂點的5個交點為A′,B′,C′,D′,E′，求證：A′,B′,C′,D′,E′共圓)等.另外，一些“圓共點”的問題也可以轉化為“點共圓”的問題得以解決.