龍鳳曲線切線的幾個有趣性質

●

(龍西路345號中301 江蘇蘇州 215128)

龍鳳曲線切線的幾個有趣性質

●錢永康張斑竹

(龍西路345號中301 江蘇蘇州 215128)

定義我們把橢圓b2x2+a2y2=a2b2和a2x2-b2y2=a2b2(agt;bgt;0)稱為龍鳳曲線(如圖1)，前者稱為龍曲線，后者稱為鳳曲線.

本文介紹龍鳳曲線切線的幾個有趣的性質.

定理1已知龍鳳曲線，過定點M(m,0)的直線l1與橢圓交于點A,B，過點M的直線l2與雙曲線交于點C,D(如圖1)，過點A，B作龍曲線的2條切線交于點P，過點C，D作鳳曲線的2條切線交于點Q，則PQ⊥x軸.

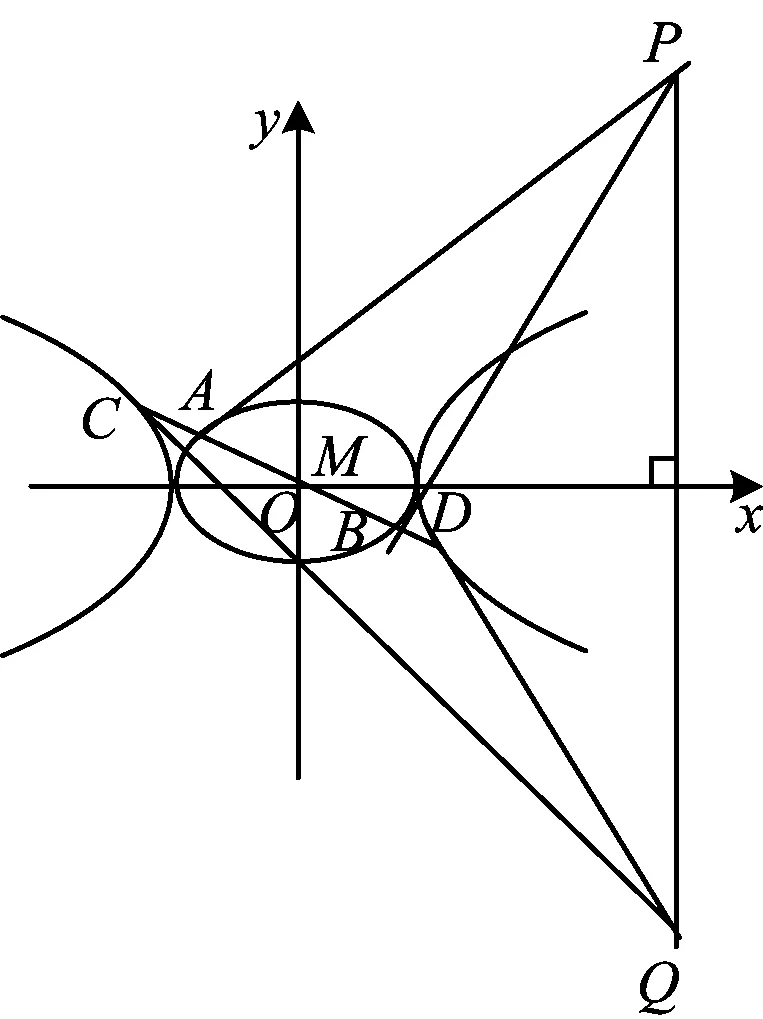
圖1

證明如圖1所示，設A(acosθ1,bsinθ1),B(acosθ2,bsinθ2)，則過點A,B的切線方程為

解得點P的坐標為

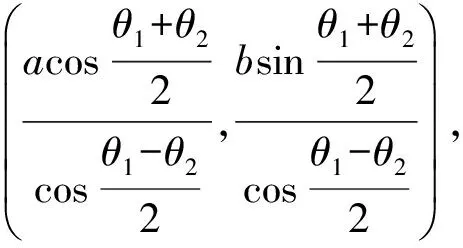
從而

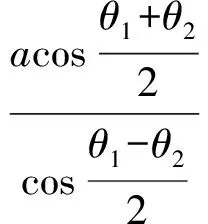
由kAM=kBM得

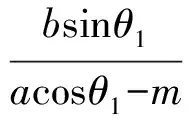
化簡得

則

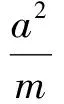
又設C(asecα1,btanα1),D(asecα2,btanα2),則過點C,D的鳳曲線的2條切線方程分別為

由kCM=kDM得

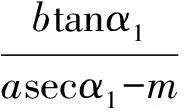
化簡得

則

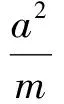
因此xP=xQ,即PQ⊥x軸.

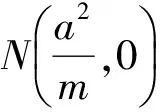
證法1設A(acosθ1,bsinθ1),B(acosθ2,bsinθ2),C(asecα1,btanα1),D(asecα2,btanα2),則

于是切點弦AB，CD的直線方程分別為

令y=0,代入上述2個方程得

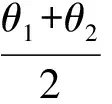
由定理1的證明知

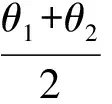
由此知

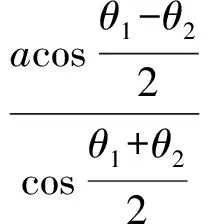
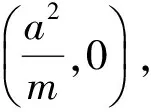
證法2設P(m,y0)，則AB，CD的直線方程分別為b2mx+a2y0y=a2b2和b2mx-a2y0y=a2b2.令y=0,得

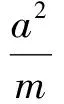
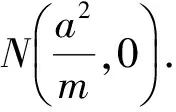
定理3已知龍鳳曲線,定點M(m,0)和N(n,0)且mn=a2，過點M,N作直線l1⊥x軸，l2⊥x軸，l1上任取一點P，作鳳曲線的2條切線PA，PB，點A，B為切點，過l2上一點Q，作龍曲線的2條切線QC，QD，C，D為切點，則AB過點N，CD過點M.

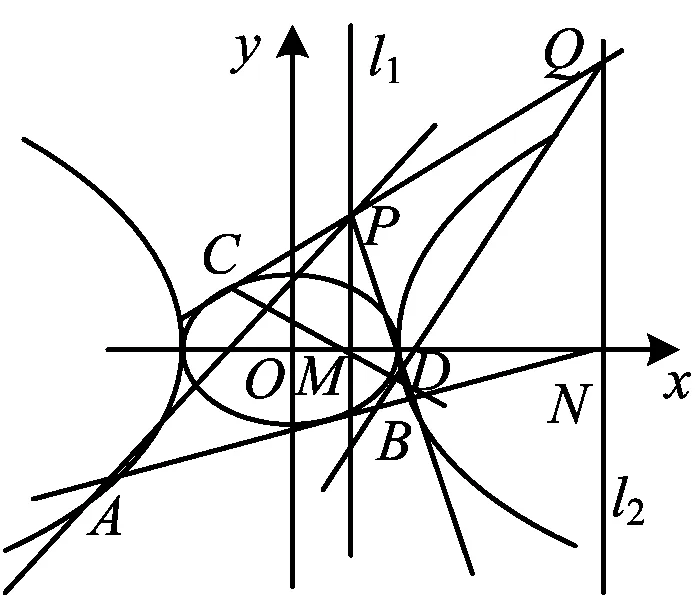
圖2

證法1如圖2所示，設C(acosθ1,bsinθ1)，D(acosθ2,bsinθ1)，得點Q的坐標為

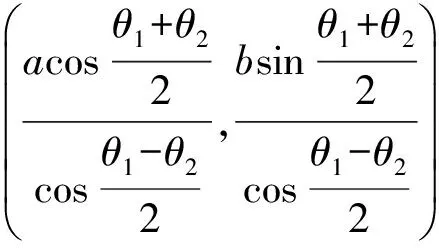
因為Q∈l2，且l2⊥x軸，所以xQ=n，即

又直線CD的方程為

令y=0得

與前式比較得

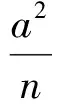
這正是點M的橫坐標，說明CD過定點M(m,0).又設A(asecα1,btanα1)，B(asecα2,btanα2)，則點P的坐標為

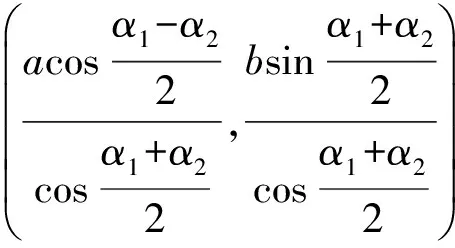
因為P∈l1,且l1⊥x軸，所以xP=xM=m,則

而直線AB的方程為

令y=0得

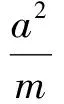
證法2設P(m,y1),Q(n,y2)，則AB,CD的直線方程為b2mx-a2y1y=a2b2和b2nx+a2y2y=a2b2.令y=0得

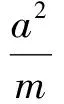
因為a2=mn,所以

xN=n,xM=m,

這說明AB過點N(n,0),CD過點M(m,0).

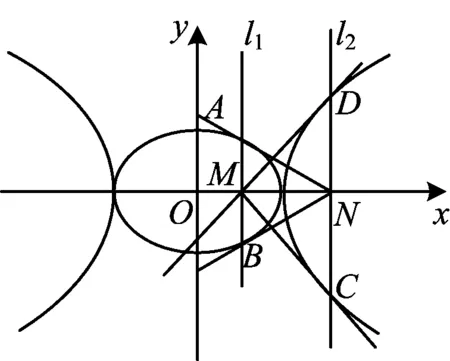
圖3

定理4已知龍鳳曲線,定點M(m,0),N(n,0)且mn=a2,過點M的直線l1⊥x軸與龍曲線交于點A，B，過點N的直線l2⊥x軸與鳳曲線交于點C,D，則A，B處龍曲線的切線均過點N，且C,D處鳳曲線的2條切線均過點M.

證明設A(acosθ1,bsinθ1)，則點A處龍曲線的切線方程為

bxcosθ1+aysinθ1=ab,

令y=0得

xcosθ1=a.

又A∈l1,且l1⊥x軸，于是acosθ1=m,代入上式得

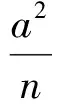
這正是點N的橫坐標，說明過點A的切線過點N.同理可得過點B的龍曲線的切線也過點N(n,0).

又設C(asecθ,tanθ)，則過點C的鳳曲線的切線方程為

bx-aysinθ=abcosθ，

令y=0得

x=acosθ.

因為C∈l2，且l2⊥x軸，所以asecθ=n，代入上式得

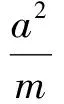
這正是點M的橫坐標，說明過點C的切線過點M(m,0).同理可知,過點D的切線也過點M.

定理5已知龍鳳曲線,定點M(m,0),N(n,0),且m·n=a2,龍曲線的長軸為AB，過點M,N的直線l1⊥x軸，l2⊥x軸，l1上一點P，連結PA，PB與鳳曲線交于點C，D，連結QA，QB與龍曲線交于點E,F，則CD過點N，EF過點M.

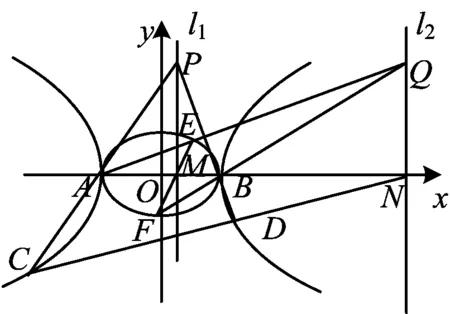
圖4

證明設A(-a,0),B(a,0)，E(acosθ1,bsinθ1)，F(acosθ2,bsinθ2)，Q(n,y0).由kAQ=kEQ和kBF=kQF,得

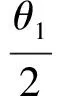
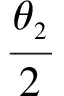
兩式相除得

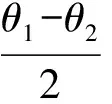
由EF的直線方程為

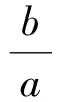
令y=0得

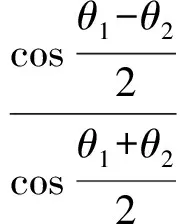
這正是點M的橫坐標,說明EF過點M(m,0).

又設C(asecθ3,btanθ3)，D(asecθ4,btanθ4)，P(m,x0).由kCA=kPA,kDB=kPB得

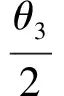
兩式相除得

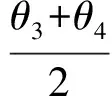
又CD的直線方程為

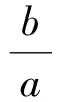
令y=0得

這正是點N的橫坐標，說明CD過點N(n,0).