第十個優美不等式的另一證明

●

(錦屏高級中學 江蘇連云港 222021)

第十個優美不等式的另一證明

●殷長征

(錦屏高級中學 江蘇連云港 222021)

文獻[1]給出了安振平教師提出的26個優美不等式中第10個不等式的具體證明.其中第10個不等式為：

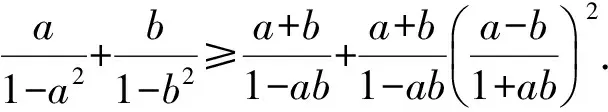
筆者經過思考探究得出另外一種證明方法，現整理如下,供大家參考.

?

?

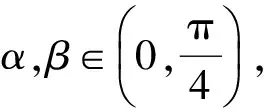
tan2α+tan2β≥2tan(α+β)[1+tan2(α-β)]

?

tan[(α+β)+(α-β)]+tan[(α+β)-(α-β)]≥2tan(α+β)[1+tan2(α-β)]

?

?

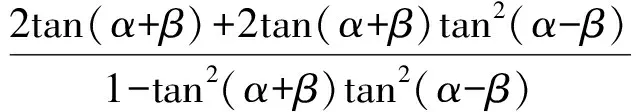
(1)

因為tan(α+β)gt;0，所以式(1)等價于

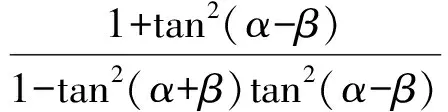
得

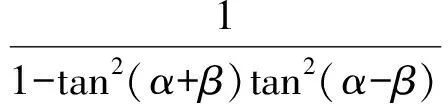
即

0≤tan2(α+β)tan2(α-β)lt;1.

顯然,0≤tan2(α+β)tan2(α-β).下面證明:tan2(α+β)tan2(α-β)lt;1.

tan2(α+β)tan2(α-β)lt;1

?

tan4α-2tan2αtan2β+4tan4β≤1-2tan2αtan2β+tan4αtan4β

?

(tan4α-1)(1-tan4β)lt;0.

(2)

[1] 尚生陳.第十個優美不等式的證明[J].中學數學教學參考(上旬)，2010(9):70.