類比思想在數學解題中的應用誤區

●

(杭州外國語學校 浙江杭州 310023)

類比思想在數學解題中的應用誤區

●趙肖東

(杭州外國語學校 浙江杭州 310023)

類比推理是由2類對象具有某些相似特征和其中一類對象的某些已知特征，推出另一類對象也具有這些特征的推理(簡稱類比).在數學中，可以由已經解決的問題和已經掌握的知識出發，通過類比推理提出新問題和作出新發現.數學家波利亞曾指出“類比是一個偉大的引路人”.高中數學新課標把培養學生的類比推理能力作為主要的能力培養目標之一.類比在發展學生創新精神的過程中有著無可比擬的價值.類比推理的創造性作用除了體現在發現新的命題，直至發現新的領域外,還可以用來發現解決問題的途徑與方法.在解決數學問題中，為尋找問題的線索往往可借助類比的方法，在類比的應用過程中，往往與解題者原有知識、經驗中類似形式或結構、類似方法或模式有聯系.類比含有猜測的成分，是或然推理，屬于合情推理的范疇，在數學思維中正是這種局限性導致學生在學習新知識、解決新問題過程中產生錯誤.本文試圖通過一些例子來探討類比推理在數學解題中的使用誤區.

1復數與實數的類比

在高中數學中，數的概念從實數集擴充到復數集后，其基本運算性質和實數的運算性質相類似，但是有些實數集中的性質就喪失了，譬如實數集中的有序性、平方的非負性等，此時再用實數集中的老辦法解決復數集中的新問題，就容易導致錯誤.

案例1

分析類比實系數一元二次方程，利用判別式判斷方程根的個數的方法來討論復系數方程根的情況是錯誤的.實系數一元二次方程ax2+bx+c=0，配方得

正解設x0為其實根，則

即

于是

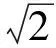
2向量與數量的類比

高中課程類比數量引入向量的概念，向量不同于數量，向量有方向，而數量的代數運算在向量范圍內不都適用，因此若將向量運算和數量運算簡單作類比，則有可能導致錯誤.

案例2

已知a，b，c是非零向量，a⊥b，x∈R，x1，x2是關于x的方程ax2+bx+c=0的2個解，求證：x1=x2． 已知x1，x2是關于x的方程ax=b(a≠0)的2個解，求證：x1=x2．方程兩邊同乘非零向量b，則b·(ax2+bx+c)=0，即b·ax2+b2x+b·c=0．因為a⊥b，所以方程可化為b2x+b·c=0．方程兩邊同乘1a，得x=-b·cb2，從而x1=x2．得x=ba，所以x1=x2．

分析實系數方程同解原理：在實系數方程中,2邊同乘非零常數，解集不變.但是將向量方程的2邊同時乘非零向量b卻不是同解變形.因為由b與ax2+bx+c垂直也可得b·ax2+b2x+b·c=0,所以b·ax2+b2x+b·c=0的解不一定是ax2+bx+c=0的解.

正解由題意得

兩式相減得

(x1-x2)[(x1+x2)a+b]=0.

因為a⊥b，所以(x1+x2)a⊥b，得

(x1+x2)a+b≠0,

故x1=x2.

3空間與平面的類比

把立體幾何知識與相關的平面幾何知識類比，是實現知識遷移的一種有效方法，同時也可以簡化運算與推理，從而優化解題過程.但是平面幾何中的定義、定理對于空間圖形不一定成立，因此兩者類比可能導致錯誤.

案例3

分析在平面幾何中有平行四邊形的判定定理：2組對邊分別相等的四邊形是平行四邊形.而在空間中，這個定理并不正確.因此該題的證明是錯誤的.

正解如圖3，在DD1上取DG=AE.由DG=AE,DG∥AE,得四邊形CGEB是平行四邊形，因此

CG=BE，CG∥BE.

從而易得△C1D1F≌△DCG(SAS)，于是

CG=D1F,CG∥D1F,

因此

BE=D1F,BE∥D1F,

圖3

故四邊形BFD1E是平行四邊形.

4圓錐曲線與圓的類比

圓是圓錐曲線中最基本、最簡單的一種圖形，與圓錐曲線在定義和幾何性質方面有很多的相似性，但由于各類曲線的差異性、特殊性，若都套用圓的解題模式，則失誤必然難免.

案例4

判斷下列橢圓和圓的位置關系：x2+2y2=8，x2+(y+2)2=4． 判斷下列兩圓的位置關系：x2+y2+2x+8y-8=0，x2+y2-4x-4y-2=0．聯立方程x2+2y2=8；x2+(y+2)2=4，{(1)聯立方程x2+y2+2x+8y-8=0；x2+y2-4x-4y-2=0，{(3)2式相減消去x，得y2-4y-8=0．(2)2式相減化簡得x+2y-1=0(4)再代入式(3)消去y得x2-2x-3=0，(5)由Δgt;0，得方程(2)有2個不同的解，則橢圓與圓有2個交點．由Δgt;0，得方程(5)有2個不同的解，則兩圓有2個交點．

分析因為式(3)等價于方程組

正解方程(2)有2個不同的解

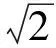
一般說來，當學生進入新知識領域時，常常會選擇熟知的、有相似特征的舊知識和方法類比地對待新知識、新問題，尋求一條快捷的解決途徑.但這有時會發生不易察覺的錯誤，上面這些例子就是如此.因此教師應采用多種方法和手段指導學生主動建構新知識，處理好新舊知識之間的聯系和區別.用好類比這把雙刃劍，對類比的過程要多加分析，去偽存真，這不但能獲得新知識，而且更重要的是它對發展學生的創新能力有著極好的促進作用.