在問題變換中引導學生做數學

●

(嘉興市第一中學實驗學校 浙江嘉興 314050)

在問題變換中引導學生做數學

●邵毓君

(嘉興市第一中學實驗學校 浙江嘉興 314050)

做數學是指運用數學知識和方法從事數學學習和解決問題的實踐活動，要求學生通過觀察分析數學事實，提出有意義的數學問題，探求適當的數學結論或規律，從而給出解釋或證明．美國數學家哈爾莫斯指出：“學習數學的唯一方法是‘做數學’”．新課程標準也指出：“力求使學生切身體會‘做數學’是學好數學的有效途徑之一”．在數學教學中，問題變換可以是把一個數學問題加以轉化、延伸或改造，得到一些新的問題，也可以是把幾個問題進行辨析、類比，找到它們之間的關系．問題變換的過程實質上是做數學的過程，它對鞏固學生基礎知識、啟迪思維、提高能力是十分有益的．本文通過實例介紹筆者是怎樣在問題變換中引導學生做數學的，供大家參考．

1問題轉化

問題轉化是解決問題的基本思想，除了把所要解決的問題轉化歸結為另一個較易解決的問題外，問題轉化也可以是問題的“一般化”和“特殊化”．“一般化”變換，就是把一個數學問題通過延伸推廣到一般形式．“特殊化”變換，就是把一個一般性的結論或題目通過賦值變形等手段，得到它的各種“特殊”形式．

例1在(x-1)(x-2)(x-3)(x-4)(x-5)的展開式中，含x4的項的系數是

( )

A．-15 B．85 C．-120 D．274

(2008年浙江省數學高考試題)

分析在教學中,可以引導學生將問題推廣為：在(x-1)(x-2)(x-3)…(x-n)的展開式中，求含xn-2的項的系數．

這個新問題可以理解成求數表A中所有數的和SA．

1·2，1·3，1·4，…,1·n

2·3，2·4，…,2·n

3·4，…,3·n

…

(n-1)·n

(數表A)

將數表A“補形”，得到數表B，考察數表B中所有數的和SB：

1·1,1·2，1·3，1·4，…,1·n

2·1,2·2,2·3，2·4，…,2·n

3·1,3·2,3·3,3·4，…,3·n

…

n·1,n·2,n·3,n·4,…,(n-1)·n

(數表B)

可以發現

SB=2SA+(12+22+32+…+n2)，

且

于是

對問題一般化，可以使學生體驗做數學的過程，同時使學生的思維在由特殊到一般、由具體到抽象的變換過程中得到發展，從而培養了學生思維的廣闊性和深刻性．

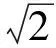
(2009年浙江省數學競賽試題)

分析可以聯系以下問題：

已知A，B，C為△ABC的3個內角，求證：

x2+y2+z2≥2xycosA+2yzcosB+2zxcosC．

這是一個重要的“母不等式”，可以由它得出許多不等式.譬如：

令x=y=z=1，得

令x=y=1,z=4，得

…

在式(2)中，令

x2+y2+z2=1，

則例2即可迎刃而解．

對問題特殊化，可以使學生在概念、定理、公式、典型問題的變換中，準確而靈活地掌握相關知識，同時培養了學生思維的靈活性．

2問題辨析

對一些似是而非的問題或解答，引導學生在改變問題條件、編擬新問題中進行剖析，從而加深認識、體驗數學.下面的例題涉及到對“數學期望”這個概念的理解．

例3甲、乙2人在一次游戲中的得分概率如表1所示，以得分多者為勝，問誰勝的希望大？

表1 得分概率表

分析 學生對這個問題給出了以下2種解法．

解法1甲得分的數學期望Eζ甲=2.1，乙得分的數學期望Eζ乙=2.2，因此

Eζ甲lt;Eζ乙，

所以乙勝的希望大．

解法2由題意得

P(甲勝)=P(甲得2分，乙得1分)+

P(甲得3分，乙得1分)+

P(甲得3分，乙得2分)=0.36,

P(乙勝)=P(乙得2分，甲得1分)+

P(乙得3分，甲得1分)+

P(乙得3分，甲得2分)=0.39．

因為

P(甲勝)lt;P(乙勝)，

所以乙勝的希望大．

在教學過程中，教師可請學生辨析這2種解法，從而引導學生改變條件中的數據來探索其正確與否．

學生1：把條件設為表2所示，其中x，ygt;0，且x+ylt;1．

表2 得分概率表

此時

Eζ甲=2.1，Eζ乙=3-2x-y；

P(甲勝)=0.6x+0.5y，

P(乙勝)=0.5-0.5x-0.1y．

比較Eζ甲和Eζ乙、P(甲勝)和P(乙勝)可知，只有在(2x+y-0.9)(1.1x+0.6y-0.5)gt;0時，2種計算結果才是一致的．特別地，取x=0.1，y=0.68，得

Eζ甲lt;Eζ乙，P(甲勝)gt;P(乙勝)，

可見此時2種計算結果是不一致的．

學生2：若將條件中的3分改為4分，則

Eζ甲=2.6，Eζ乙=2.5；

P(甲勝)=0.36，P(乙勝)=0.39．

因此

Eζ甲gt;Eζ乙，P(甲勝)lt;P(乙勝)．

可見此時2種計算結果也是不一致的．

學生3：我認為在這2種解法中，解法2是正確的，得分的數學期望大不一定勝率就大．

教師：很好，數學期望和勝率是從不同層面上來反映甲、乙得分差異的．Eζ甲gt;Eζ乙表示游戲中甲得分的平均水平要高于乙，P(甲勝)gt;P(乙勝)表示一次游戲中甲得分高于乙比乙高于甲的可能性大．

在這個例子中，教師引導學生改變問題的條件，在對各種不同情形的辨析過程中加深了對數學期望的理解.在教學中，可以通過舉例、辨析、判斷等方法來研究問題，經常進行這樣的分析和思考，有助于學生深刻理解問題并抓住本質．

3問題類比

類比是探索問題、解決問題與發現新結果的一種卓有成效的思維方法．在數學中，類比是發現概念、方法、定理和公式的重要手段，也是開拓新領域和創造數學新分支的重要途徑．

(2008年江西省數學高考試題)

圖1

分析此題可以類比圓的有關切點弦的知識：若過圓x2+y2=r2外一點P(x0,y0)作圓的2條切線，切點為A,B，則直線AB(切點弦)的方程為x0x+y0y=r2．

x1x-y1y=1.

同理可得,PB的方程為x2x-y2y=1．因為點P(m，y0)在切線PA，PB上，所以

mx1-y0y1=1,mx2-y0y2=1．

可以引導學生進一步研究下例：

(2007年全國高中數學聯賽試題)

用類比思想可以發現相關問題的聯系，找到問題解決的辦法，增強學生解題的信心．在數學教學中，學生不斷嘗試并靈活地運用類比，將會對學習數學、運用數學解決實際問題乃至學生的思維方式產生深遠的影響．

4問題改造

數學問題的改造是指在一道題的基礎上進行多角度、多層次的變式教學．改造、強化等是培養學生創造性能力的有力工具，可以調動學生思維的積極性，將學生領進數學的神秘殿堂．

例6對任意正數x,y，求證：

通過上面的例子可以發現,問題變換主要經歷以下4個環節：提出問題——聯想(猜想)——證明——提出新問題.這樣的過程不再是簡單的做數學題了.在這樣的做數學的過程中，通過一串串的問題變換，引導學生解決問題、提出新問題、探尋幾個問題之間的關系，培養學生發現問題、提出問題和解決問題的能力，提高學生的創新精神和實踐能力．問題的不斷變換是做數學的靈魂，在問題變換中引導學生做數學是一種新的學習方式，要求學生采用自主探索、大膽猜測、合作交流、積極思考等活動方式.在平時的學習中，要善于從教材的例題、習題等內容去變、去引申、去探索．這種學習方式也對教師提出了更高要求，要求教師不斷學習、加強研究、提高自身素質，利用類似的問題提供豐富的可供學生研究的素材．