在探究中升華數學習題的價值

●

(瓶窯中學 浙江杭州 311115)

在探究中升華數學習題的價值

●陳建美

(瓶窯中學 浙江杭州 311115)

荷蘭數學教育家弗賴登塔爾曾說過：“數學教學方法的核心是學生的‘再創造’”.數學教學不僅要讓學生獲得知識，更重要的是讓學生擁有智慧、學會思考和再創造.知識關乎事物，智慧關乎人生，知識能看到一塊石頭就是一塊石頭，一粒沙子就是一粒沙子，做一道習題算一道習題，智慧則能從石頭和沙子中看到風景，從習題中得到啟發，獲得創新的靈感.

數學探究是高中數學新課程中引入的一種新的學習方法，通過對習題的探究，有助于實現知識的再創造，培養學生的數學思考能力.如何對習題進行探究呢？通常可以改變命題的條件或結論，在類比中引導學生的探究過程.

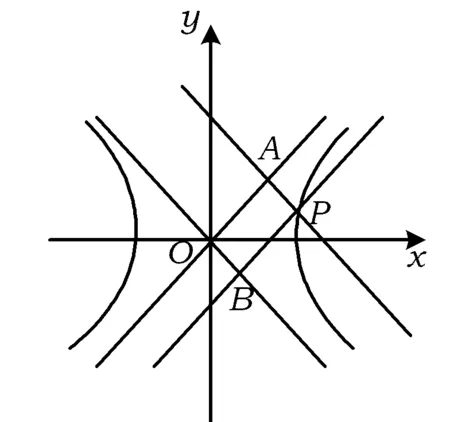
圖1

分析如圖1所示，要求平行四邊形PAOB的面積，關鍵是要知道動點P的坐標.為方便解題,不妨設點P(asecθ,btanθ)(θ∈R),由此可求出點A，B的坐標，進而求出平行四邊形PAOB的面積.

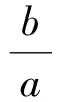
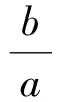
因為點P到直線OA的距離為

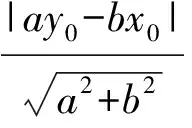
所以平行四邊形PAOB的面積為

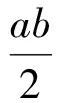
故如此構造的平行四邊形的面積是定值，即為雙曲線的實半軸和虛半軸積的一半.

因此

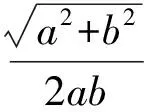
從而平行四邊形PAOB的面積為

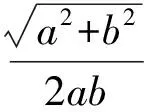
因為

(ay0+bx0)(ay0-bx0)lt;0,

于是平行四邊形PAOB的面積為

S=|OA|·A=

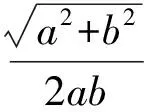
即

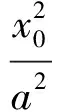
問題研究到這里好象可以結束了，但如果再用類比的方法去探究，又可得到以下性質(由雙曲線類比到橢圓).

解設動點P(acosθ,bsinθ)(θ∈R),則平行線PA的直線方程為

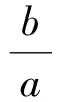
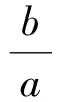
于是平行四邊形PAOB的面積為

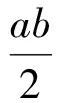
如此構造的平行四邊形的面積最大值為橢圓的長半軸和短半軸積的一半.

圖2

(1)|OM|·|ON|=a2為定值；

(2)|OQ|·|OR|=b2為定值.

平行線PR的直線方程為

令y=0,則

|OM|=|asecθ-atanθ|,|ON|=|asecθ+atanθ|,

得|OM|·|ON|=a2為定值.同理令x=0,可得|OQ|·|OR|=b2為定值.

證明(1)設點P(x0,y0)，直線l1′,l2′過點P且與l1,l2分別平行，則直線l1′的方程為

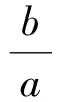
直線l2′的方程為

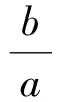
令y=0,得

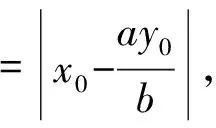
由|OM|·|ON|=a2得

又因為點M，N在x軸的同向，所以

即

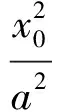
(1)|OM|2+|ON|2=2a2為定值；

(2)|OQ|2+|OR|2=2b2為定值.

一個看似平談的雙曲線習題經過了深入的探究和知識的再創造，歸納類比出曲線的其他性質，實現了知識的創新，有力地激發了學生的學習興趣，啟發了學生如何以已有的數學知識和經驗為基礎對知識進行再創造的過程.教師要創造合適的條件，提供更多、更好的具體案例，讓學生在實踐的過程中，自己探究出各種數學的性質，讓學生的各種思維能力(歸納類比、演繹證明、反思與建構等)得到充分的鍛煉.