NPC問題中幾個基本定理的證明

郭 蕾

(常州紡織服裝職業技術學院信息技術系，江蘇 常州 213164)

NPC問題中幾個基本定理的證明

郭 蕾

(常州紡織服裝職業技術學院信息技術系，江蘇 常州 213164)

就NPC問題(NP-complete，NP完全問題)中的幾個基本定理給出了證明。首先從基本的團問題、SAT問題和圖的著色問題入手，證明了它們都屬于NPC問題，再利用獨立集、頂點覆蓋、有向圖、團、SAT和圖的著色等問題本身的內在關系，對其他的定理做了一一證明。

NPC問題；SAT；著色；獨立集；頂點覆蓋；有向圖；無向圖；哈密頓道路；回路

1 團的問題屬于NPC問題

若G1完全圖是G的子圖，則G1稱為G的團。

團的問題描述如下：已知圖G和正整數k,圖G是否有k個頂點的團？

將SAT問題化為團的問題，方法如下:合取范式中每個變元及其非的一次出現對應于一個圖中的頂點,不在同一子句且不互非的變元對應的頂點以邊相連。 設合取范式的子句數為k,問題就轉化為對應的圖是否有k個頂點的團。

2 3SAT問題屬于NPC問題

對于一個合取范式，若每個子句有且僅有3個變元時，它的可滿足性問題便稱為3SAT問題。接下來說明3SAT問題屬于NPC問題。

證明因為3SAT是SAT的特殊情況， 所以它屬于NP問題。 下證SAT∝3SAT。

1) 短→長:

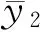
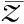
2)長→短:

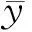
(a)可滿足?(b)可滿足，故得證。

3 圖的著色問題屬于NPC問題

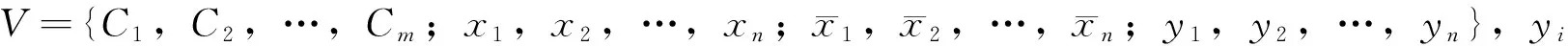
設k=n+1，給定k種顏色，下證f可滿足?G可n+1著色。

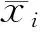
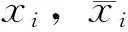
4 獨立集和頂點覆蓋問題屬于NPC問題

圖G=(V,E)，設S?V，S中任意2點都不相鄰，則稱S為G的獨立集。設C?V，與C中點關聯的邊集就是E，則稱C為G的頂點覆蓋。

獨立集問題描述如下：G=(V,E)，k∈Z+，是否存在獨立集S，使得|S|≥k；

頂點覆蓋問題描述如下：G=(V,E)，k∈Z+，是否存在頂點覆蓋C，使得|C|≤k。

定理1獨立集問題屬于NPC問題。

定理2頂點覆蓋問題屬于NPC問題。

證明下面證明獨立集問題∝頂點覆蓋問題。G=(V，E)，k∈Z+，另l=|V|-k，若有獨立集S，|S|≥k,則V-S是G的覆蓋,V-S的頂點個數為|V|-|S≤|V||-k=l。反之，若C是G的頂點覆蓋，|C| ≤l，則C=V-C是獨立集。

5 有向圖的哈密頓道路和回路問題屬于NPC問題

哈密頓道路問題描述如下：已知有向圖D=(V,A)以及u,v∈V，是否存在從u到v的哈密頓道路，使V中所有點到且僅到一次。

定理3有向圖的哈密頓道路問題屬于NPC問題。

下面證明頂點覆蓋問題∝有向圖的哈密頓道路問題。

故對應于頂點v∈V，存在一條道路：

↑↓ ↑↓

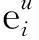
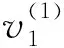
若圖G中有(u,v)∈E，則G′圖中存在從ai到aj的道路：

和:

圖G′存在有哈密頓道路的充要條件是圖G有k個頂點的(極小)頂點覆蓋。

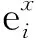
2)“?”：若G′有哈密頓道路，則必從a0起到ak止，且過所有的ai，0

推論1有向圖的哈密頓回路問題屬于NPC問題。哈密頓回路問題是NP問題。下面證明哈密頓道路問題∝哈密頓回路問題。構造D′=(V′,A′)，V′=V∪{x}，A′=A∪{(x,u),(v,x)}。于是D有哈密頓道路當且僅當D′有哈密頓回路。故哈密頓回路問題是NPC的。

6 無向圖的哈密頓道路問題屬于NPC問題

定理4無向圖的哈密頓道路問題屬于NP問題。

下面證明有向圖的哈密頓道路問題∝無向圖的哈密頓道路問題。

設已知有向圖G=(V,E)，構造G的一個對應的無向圖G′=(V′,E′)如下：

V′={v1,v2,v3|v∈V}E′={(v1,v2),(v2,v3)|v∈V}∪{(u3,u1)|(u,v)∈E}

下證G有哈密頓道路?G′有哈密頓道路。

[1]Dorit S H.Approximation Algorithms for NP-Hard Problems[M].北京：世界圖書出版公司， 1998.

[2] 陳志平，徐宗本.計算機數學[M].北京：科學出版社，2001.

[3] 黃文奇，許如初.近世計算理論導引:NP難度問題的背景、前景及其求解算法研究[M].北京：科學出版社，2004.

[4] 王樹禾.圖論[M].北京：科學出版社，2009.

[編輯] 洪云飛

10.3969/j.issn.1673-1409.2011.12.008

O157.5

A

1673-1409(2011)12-0019-03