一類非線性二層規(guī)劃問題的神經(jīng)網(wǎng)絡(luò)方法

洪云飛

(長江大學(xué)期刊社；長江大學(xué)信息與數(shù)學(xué)學(xué)院，湖北 荊州 434023)

呂一兵

(長江大學(xué)信息與數(shù)學(xué)學(xué)院，湖北 荊州 434023)

一類非線性二層規(guī)劃問題的神經(jīng)網(wǎng)絡(luò)方法

洪云飛

(長江大學(xué)期刊社；長江大學(xué)信息與數(shù)學(xué)學(xué)院，湖北 荊州 434023)

呂一兵

(長江大學(xué)信息與數(shù)學(xué)學(xué)院，湖北 荊州 434023)

研究了下層為凸規(guī)劃的一類非線性二層規(guī)劃問題的神經(jīng)網(wǎng)絡(luò)方法。在下層問題為凸規(guī)劃的情況下,將下層問題用其K-T最優(yōu)性條件代替，從而把原二層規(guī)劃轉(zhuǎn)化為單層非線性規(guī)劃；構(gòu)造該單層規(guī)劃的罰函數(shù)，提出求解該類規(guī)劃問題的神經(jīng)網(wǎng)絡(luò)方法。數(shù)值試驗(yàn)結(jié)果表明該方法是可行和有效的。

非線性二層規(guī)劃；罰函數(shù)；K-T最優(yōu)性條件；神經(jīng)網(wǎng)絡(luò)

在對多層規(guī)劃的研究中，二層規(guī)劃是一個(gè)重要的研究對象。二層規(guī)劃研究的是具有2個(gè)層次系統(tǒng)的規(guī)劃與管理問題，上層決策者只是通過自己的決策去指導(dǎo)下層決策者，并不直接干涉下層的決策；而下層決策者只需要把上層的決策作為參數(shù)，它可以在自己的可能范圍內(nèi)自由決策。二層規(guī)劃的基本形式為：

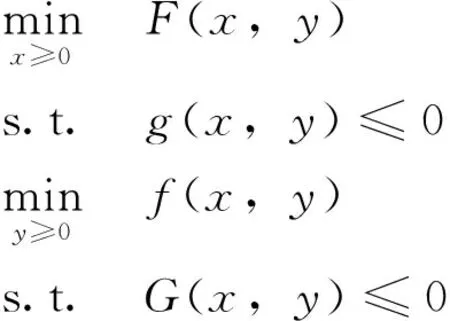
式中，x、y分別稱為上下層變量；F、f分別稱為上下層目標(biāo)函數(shù)；g、G分別稱為上下層約束函數(shù)。當(dāng)F、f、G、g全為線性函數(shù), 則稱為線性二層規(guī)劃；否則稱為非線性二層規(guī)劃。

一般來說，求解二層規(guī)劃問題是非常困難的，文獻(xiàn)[1]指出線性二層規(guī)劃是一個(gè)Np-hard問題，文獻(xiàn)[2-4]對此結(jié)論給出了證明。對于一般的非線性二層規(guī)劃問題, 文獻(xiàn)[5-6]提出了基于下層問題的K-T最優(yōu)性條件的求解方法。下面筆者主要研究F、f、G、g連續(xù)可微且f、G關(guān)于變量y是凸函數(shù)的一類非線性二層規(guī)劃問題：鑒于文獻(xiàn)[5-6]中的方法，將下層問題用其K-T最優(yōu)性條件代替，從而將原二層規(guī)劃化為單層非線性規(guī)劃, 構(gòu)造該單層規(guī)劃的罰函數(shù)，進(jìn)而提出求解該類規(guī)劃問題的神經(jīng)網(wǎng)絡(luò)方法。

1 非線性二層規(guī)劃問題的轉(zhuǎn)化

考慮如下線性約束的非線性二層規(guī)劃問題：

其中，x∈Rn，y∈Rm，F(xiàn):Rn×m→R1，f:Rn×m→R1，P∈R(n+m)×(n+m)，c∈Rn，d∈Rm，Q∈Rm×m，D∈Rm×n，b∈Rm，A∈Rq×n，B∈Rq×m，r∈Rq。

定義1對于線性二層規(guī)劃問題，稱集合：

S={(x,y)|Ax+By-r≤0,x≥0,y≥0}

為其約束域。

對于固定的x，當(dāng)下層問題滿足Slater條件，由凸規(guī)劃的最優(yōu)性理論可知，下層規(guī)劃問題可以轉(zhuǎn)化等價(jià)如下Kuhn-Tucker最優(yōu)性條件穩(wěn)定點(diǎn)問題：

Qy+Dx+b+λTB=0λT(Ax+By-r)=0λ≥0Ax+By-r≤0

(2)

式中，λ=(λ1,…,λq)T是廣義拉格朗日乘子。用式(2)替換式(1)中的下層問題得：

記h(x,y,λ)=(Qy+Dx+b+λTB,λT(Ax+By-r))T，則問題(3)可簡寫為下格式：

2 非線性二層規(guī)劃問題的神經(jīng)網(wǎng)絡(luò)模型

定義2問題(4)的罰函數(shù)[7]定義為：

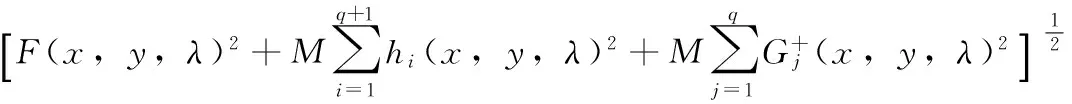
(5)

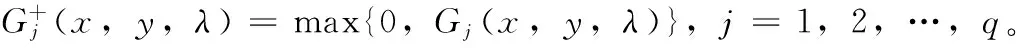
由此問題(4)可以對應(yīng)轉(zhuǎn)化為如下罰函數(shù)優(yōu)化問題：

記X=(x,y,λ)T，由式(5)則可定義其能量函數(shù)[7,8]為：

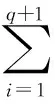
(6)

根據(jù)神經(jīng)網(wǎng)絡(luò)理論，將優(yōu)化設(shè)計(jì)變量與神經(jīng)元輸出相對應(yīng)，構(gòu)造神經(jīng)網(wǎng)絡(luò)的非線性微分方程(動(dòng)力系統(tǒng))為：

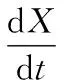
(7)

由式(6)和式(7)可得到能量函數(shù)隨時(shí)間的變化率為：

(8)

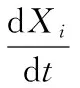
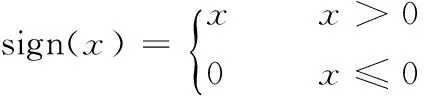
因此，式(7)可以具體化為：

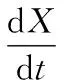
(9)

定理1若X*是網(wǎng)絡(luò)動(dòng)力系統(tǒng)(7)或(9)在罰因子M下的平衡點(diǎn)，對于X≠0有E(X)≠0，則X*是網(wǎng)絡(luò)動(dòng)力系統(tǒng)(7)或(9)的穩(wěn)定點(diǎn)，且為罰函數(shù)優(yōu)化問題的局部最優(yōu)點(diǎn)。若X*是罰函數(shù)優(yōu)化問題的一個(gè)最優(yōu)解，則X*是網(wǎng)絡(luò)動(dòng)力系統(tǒng)(7) 或(9)的在罰參數(shù)M下的平衡點(diǎn)。

定理1前一部分由式(8)可知是成立的，后一部分顯然成立。

3 數(shù)值試驗(yàn)

考慮其理論最優(yōu)解為如下的非線性二層規(guī)劃問題:

使用定步長四階龍格庫塔法求解上述問題的神經(jīng)網(wǎng)絡(luò)動(dòng)態(tài)方程(9)。選取初值為(x,y,λ1,λ2,λ3)=(5，5，1，1，1)，罰因子M=10000，步長為10-5，得到圖1。

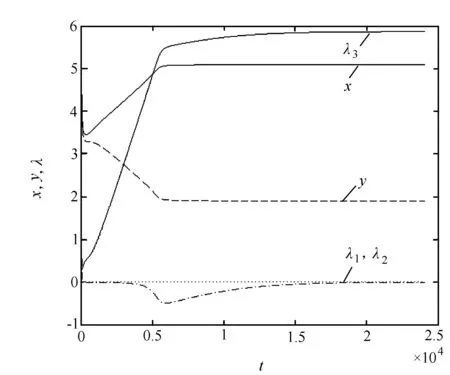
圖1 x、y、λ隨時(shí)間的變化曲線

從圖1中可以看到曲線最終都達(dá)到穩(wěn)定狀態(tài)，由該方法得到最終的計(jì)算結(jié)果為(x,y,λ1,λ2,λ3)=(5.104，1.891，0.000，-0.000，5.870)，所以用神經(jīng)網(wǎng)絡(luò)方法求得的優(yōu)化解為(x,y)=(5.104，1.891)。數(shù)值試驗(yàn)結(jié)果表明，神經(jīng)網(wǎng)絡(luò)最終達(dá)到穩(wěn)定狀態(tài)，可以得到非線性二層規(guī)劃問題的最優(yōu)解。

4 結(jié) 語

給出了下層為凸規(guī)劃的一類非線性二層規(guī)劃問題的神經(jīng)網(wǎng)絡(luò)方法，該算法的設(shè)計(jì)比較簡單，易于編程實(shí)現(xiàn)，同時(shí)值得注意的是利用罰函數(shù)構(gòu)造神經(jīng)網(wǎng)絡(luò)模型使得系統(tǒng)變量較少，同時(shí)可增大罰因子的值以加快網(wǎng)絡(luò)的收斂速度。但是在數(shù)值試驗(yàn)的過程中，選取不同的初值對神經(jīng)網(wǎng)絡(luò)的最終穩(wěn)定狀態(tài)有不同的影響，尤其當(dāng)選取決策變量的初值較小時(shí)，將得不到最優(yōu)解的穩(wěn)定狀態(tài)，而且罰因子過小起不到懲罰作用，過大又受機(jī)器性能影響。因此，該非線性二層規(guī)劃問題的神經(jīng)網(wǎng)絡(luò)方法的全局穩(wěn)定性研究方面以及初值有待進(jìn)一步深入。

[1]Jeroslow R.The polynomial hierarchy and a simple model for competitive analysis[J].Mathematical programming，1985，32(2)：146-164.

[2]Ben-Ayed O，Blair C E.Computational difficulties of bilevel linear programming[J].Operations Research，1990，38(3)：556-560.

[3]Bard J.Some properties of the bilevel programming problem [J].Journal of Optimization Theory and Applications.1991，68(2)：371-378.

[4]Hansen P，Jaumard B，Savard G.New branch and bound rules for linear bilevel progra-mming [J].SIAM Journal scientific and statistical computing，1992，13(5)：1194-1217.

[5] Lv Yibing，Hu Tiesong，Wang Guangmin，et al.A penalty function method based on Kuhn-Tucker condition for solving linear bilevel programming[J].Applied Mathematics and Computation，2007，188(1)：808-813.

[6]呂一兵，陳忠，萬仲民，等.非線性-線性規(guī)劃問題的罰函數(shù)方法[J].系統(tǒng)科學(xué)與數(shù)學(xué)，2009，29(5)：630-636.

[7]孟志青，胡奇英，楊曉琪.基于精確罰函數(shù)的一類廣義非線性神經(jīng)網(wǎng)絡(luò)模型[J].自動(dòng)化學(xué)報(bào)，2003，29(5)：755-760.

[8]任麗君.基于罰函數(shù)法的神經(jīng)網(wǎng)絡(luò)優(yōu)化設(shè)計(jì)研究[J].紹興文理學(xué)院學(xué)報(bào)，2006，26(10)：36-39.

[編輯] 李啟棟

10.3969/j.issn.1673-1409.2011.12.002

O224

A

1673-1409(2011)12-0004-03