具變指標(biāo)反應(yīng)項(xiàng)的拋物和雙曲方程的爆破性質(zhì)

唐樹(shù)喬

(東南大學(xué)數(shù)學(xué)系，江蘇 南京 211100; 亳州師范高等專(zhuān)科學(xué)校理化系，安徽 亳州 236800)

具變指標(biāo)反應(yīng)項(xiàng)的拋物和雙曲方程的爆破性質(zhì)

唐樹(shù)喬

(東南大學(xué)數(shù)學(xué)系，江蘇 南京 211100; 亳州師范高等專(zhuān)科學(xué)校理化系，安徽 亳州 236800)

研究了帶有變指標(biāo)反應(yīng)項(xiàng)的非線性拋物和雙曲方程正解的爆破性質(zhì)，證明了存在初值使得相應(yīng)解在有限時(shí)刻爆破。

爆破；變指標(biāo)；非線性拋物方程；非線性雙曲方程

對(duì)非線性拋物方程:

(1)

有學(xué)者對(duì)方程(1)解的爆破問(wèn)題進(jìn)行了大量深入的研究，如爆破準(zhǔn)則、爆破的速率和剖面、最大存在時(shí)間、爆破后的連續(xù)性等[1-2]。拋物問(wèn)題(1)出現(xiàn)在應(yīng)用數(shù)學(xué)的好幾個(gè)分支中，并且已經(jīng)應(yīng)用到化學(xué)反應(yīng)模型、熱傳學(xué)和群體力學(xué)。

考慮下列既帶有變指標(biāo)反應(yīng)項(xiàng)又帶有固定指標(biāo)反應(yīng)項(xiàng)的非線性拋物方程：

(2)

其中，Ω?RN是帶有光滑邊界?Ω的有界區(qū)域；k>1；q>1；p(x)和u0(x)是非負(fù)連續(xù)有界函數(shù)且u0(x)不恒等于0。近年來(lái)，帶有變指標(biāo)反應(yīng)項(xiàng)的非線性拋物方程得到了人們的廣泛關(guān)注[3-6]。對(duì)于k=-1時(shí)方程(2)的情形，劉云霞[7]也給出了解在有限時(shí)刻爆破和整體存在的條件。令：

筆者研究了帶有變指標(biāo)反應(yīng)項(xiàng)的非線性拋物和雙曲方程正解的爆破性質(zhì)，證明了存在初值使得相應(yīng)解在有限時(shí)刻爆破。

1 非線性拋物方程

1.1有限時(shí)刻爆破

引理1設(shè)η(t)為連續(xù)可導(dǎo)函數(shù)且滿足不等式：

η′(t)≥-aη(t)+bηq(t)-c

其中，常數(shù)q>1,a,b,c>0。若η(0)>0,-aη(0)+bηq(0)-c>0，則η(t)爆破。

定理1設(shè)Ω?RN是帶有光滑邊界?Ω的有界區(qū)域，u(x,t)是方程(2)的正解，p(x)和u0(x)是非負(fù)連續(xù)有界函數(shù)，那么當(dāng)p->q>1時(shí)，對(duì)于充分大的初值u0(x)，存在有限時(shí)間T>0使得:

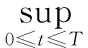
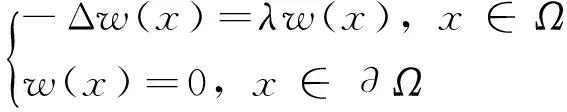
(3)

對(duì)于每一個(gè)t>0，把Ω分成2個(gè)集合：

Ω1={x∈Ω:u(x,t)<1}Ω2={x∈Ω:u(x,t)≥1}

于是：

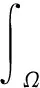
根據(jù)Ω2的定義，可以得到：

(4)

其中c2>0。令：

聯(lián)合不等式(3)和(4)可得：

η′(t)≥-λ1η(t)+εηq(t)-c2

于是，由引理1可以知道，方程(2)的正解u(x,t)在有限時(shí)刻爆破。

1.2整體存在性

定理2設(shè)Ω?RN是帶有光滑邊界?Ω的有界區(qū)域，p(x)是非負(fù)連續(xù)有界函數(shù)，那么當(dāng)p(x)≤1時(shí)，方程(2)的正解u(x,t)對(duì)任意初值整體存在。

證明當(dāng)p(x)≤1時(shí)，構(gòu)造函數(shù)v(x,t)=(‖u0‖∞+1)et。則：

vt(x,t)=(‖u0‖∞+1)et≥(‖u0‖∞+1)p(x)etp(x)≥Δv+vp(x)-kuq

且：

v(x,0)=‖u0‖∞+1≥u0v(x,t)=(‖u0‖∞+1)et≥0x∈?Ω

從而v(x,t)為方程(2)的上解，所以方程(2)的正解u(x,t)對(duì)任意初值整體存在。

2 非線性雙曲方程

下面，筆者將討論以下非線性雙曲方程：

(5)

的正解在有限時(shí)刻爆破的性質(zhì)。其中，u0(x)≥0,u1(x)≥0,并且它們都不恒等于0。

引理2[8]設(shè)y(t)∈C2滿足y″≥h(y(t))，y(0)=α>0,y′(0)=β>0,對(duì)于所有的s≥α都有h(s)≥0，那么y′(t)>0且：

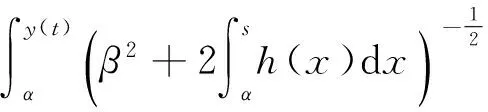
定理3設(shè)u(x,t)∈C2是方程(5)的解，p(x)是非負(fù)連續(xù)有界函數(shù)，那么當(dāng)p->q>1時(shí)，對(duì)于充分大的初值u0(x)和u1(x)，存在有限時(shí)間T>0使得：

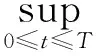
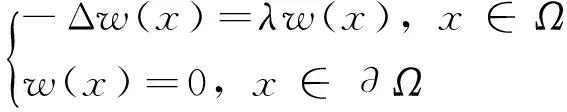
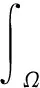
由H?ld不等式，可以推知：

(6)

對(duì)于每一個(gè)t>0，把Ω分成2個(gè)集合：

Ω1={x∈Ω:u(x,t)<1}Ω2={x∈Ω:u(x,t)≥1}

根據(jù)Ω2的定義，可以得到:

(7)

其中c2>0。由不等式(6)和(7)可得:

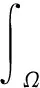
η″(t)≥-λ1η(t)+εηq(t)-c2

當(dāng)α=η(0)充分大時(shí)，應(yīng)用引理2可得-λ1η(t)+εηq(t)-c2>0，再注意到:

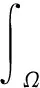
因此:

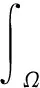
于是定理3得證。

[1]Pao C V.Nonlinear Parabolic and Elliptic Equations[M]. New York：Plenum Press, 1992.

[2] Samarskii A A, Galaktionov V A, Kurdyumov S P，et al. Blow-up in Quasilinear Parabolic Equations[M]. New York:Walter de Gruyter, 1995.

[3] Antontsev S N, Shmarev S I.Existence and uniqueness of solutions of degenerate parabolic equations with variable exponents of nonlinearity[J].J Math Sci, 2008,150:2289-2301.

[4] Antontsev S N, Shmarev S I.A model porous medium equation with variable exponent nonlinearity: existence, uniqueness and localization properties of solutions[J]. Nonlinear Anal,2005,60:515-545.

[5] Pinasco J P.Blow-up for parabolic and hyperbolic problems with variable exponents[J].Nonlinear Anal，2009,71:1094-1099.

[6] Bai Xue-li,Zheng Si-ning. A semilinear parabolic system with coupling variable exponents[J]. Annali di Mathematic Pura ed Application,2011,190 (3): 525-537.

[7] 劉云霞.帶有變指標(biāo)反應(yīng)項(xiàng)的半線性拋物方程的臨界指標(biāo)[D].大連:大連理工大學(xué),2009.

[8] Glassey R T.Blow-up theorems for nonlinear wave equations[J].Math Z, 1973,132: 183-203.

[編輯] 洪云飛

10.3969/j.issn.1673-1409.2011.12.001

O175.2

A

1673-1409(2011)12-0001-03