風力機變槳系統單神經元自適應PID控制

任海軍, 何玉林

(重慶大學機械傳動國家重點實驗室,重慶400030)

通常將變速變槳風力發電系統劃分為三個控制區域[1-3],分別為啟動階段(區域1)、額定風速以下階段(區域2)和額定風速以上階段(區域3).區域1的控制要求較少,主要的控制集中在區域2和區域3.區域2的控制目標是通過控制電機轉矩來保持風機以最佳葉尖速比運行,以此獲得最大功率.區域3的控制目標是通過變槳距調節使風力機輸出功率保持恒定.學者們對額定風速以上恒定風力機輸出功率的控制進行了大量研究工作,如根據奇異擾動理論和逆系統方法設計的非線性風力機槳距角控制器,采用帶靈敏度成型法的極點配置來設計魯棒數字R-S-T槳距角控制器,還有的將最優控制方法、神經網絡和模糊控制等方法運用到槳距角的控制中,都取得了一定的控制效果[4-10].文獻[7]采用神經網絡設計變速變槳距風力機的槳距角控制器,在風力機運行過程中,運用多層感知器和徑向基函數神經網絡進行觀測.文獻[8]采用PID算法設計了定速主動失速型風力機槳距角控制器,試驗表明,在風力機運行風速的大部分范圍,都會產生剛性頻率振蕩阻尼,使得槳距角的變槳速率受到限制.文獻[9]通過系統辨識的方法獲得變速風力機的自適應模糊控制器,利用獲得的控制器對實際數據進行處理,連續優化內部參數,以此補償系統非線性和控制過程的時變特性.

PID控制器由于其結構簡單、控制可靠等特點在工業中得到廣泛應用,但其比例、積分、微分系數的調節是個難點,很難滿足非線性系統的控制需要.單神經元控制器具有自學習和自適應能力,不但結構簡單,而且能夠適應環境變化,易于實現.因此,將單神經元方法和PID控制結合,利用單神經元方法對PID參數進行在線調節,使構成的單神經元PID控制器具有兩種控制方法的優點,可將其運用到風力機槳距角的控制中.通過仿真,驗證了設計的風力機槳距角單神經元自適應PID控制器對系統的控制性能.

1 風力機能量轉換原理

當風通過風力機時推動風力機葉片旋轉,將風能轉換為機械能.風力機獲得的能量為[11]:

式中:P為風力機輸出的軸功率;T為風力機轉矩;ω為風力機角速度;ρ為空氣密度;v為來流風速;S為風力機掃掠面積;Cp為能量轉換系數(即功率系數).

從式(1)可以看出,當風力機型號選定后,其獲得的能量由風速和能量轉換系數確定.當風速高于額定風速后,如果要保持風力機輸出功率不變,則需要改變系統的功率系數.功率系數與葉尖速比和槳距角的函數關系為[11]:

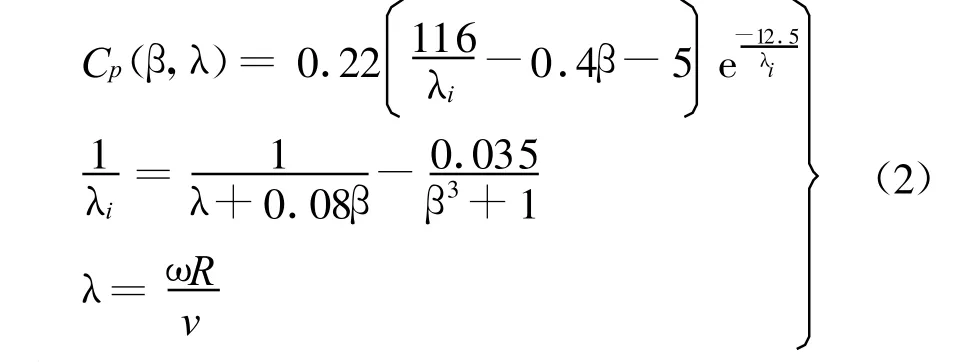
式中:β為槳距角;λ為葉尖速比;λi為λ和β的函數;e為常數;R為風輪半徑.

由式(1)和式(2),并結合葉尖速比-風能轉換系數-槳距角關系曲線族圖(圖1),說明 λ、Cp和β三者間的關系.當風力機功率轉換系數為Cp1時,在圖中有4個交點,分別為A、B、C、D.與槳距角為0°的曲線交于點A和C,點A和C分別對應葉尖速比λ1和 λ3,且 λ1＜λ3;與槳距角為2°的曲線交于點B和D,點B和D分別對應葉尖速比λ2和λ4,且λ2＜λ4.可以看出,通過改變槳距角和葉尖速比的方式可以使風力機功率轉換系數保持在某一恒定值.當葉尖速比為λ2時,產生的交點B和E分別對應槳距角0°和2°,對應的功率轉換系數Cp1＜Cp2.又可看出,若保持葉尖速比不變,調節槳距角大小,可以得到不同的功率系數.在曲線AE段,槳距角大小不變,調節葉尖速比值,可以得到不同的功率系數.因此,通過調節槳距角或葉尖速比可以得到不同的功率系數,從而能夠進一步調節風力機的輸出功率.

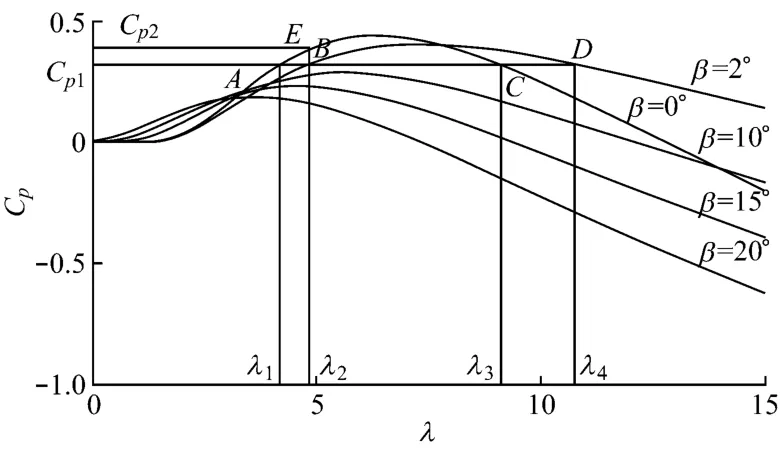
圖1 葉尖速比-風能轉換系數-槳距角關系曲線族圖Fig.1 Relationship among tip speed ratio,wind energy conversion factor and pitch angle

2 變槳距系統建模

忽略風力機的剛性系數、阻尼系數和齒輪箱的慣性,變速變槳距風力機模型為[4]:

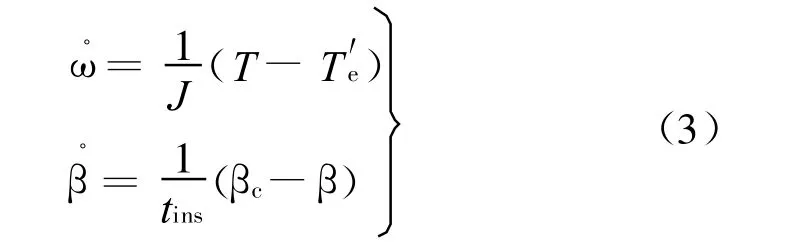
式中:ω·為角加速度;J為風輪轉動慣量;T′e為折算到低速軸的轉矩;β·為槳距角實際值時的角加速度;tins為變槳機構時間常數;βc為槳距角命令值;β為槳距角實際值.

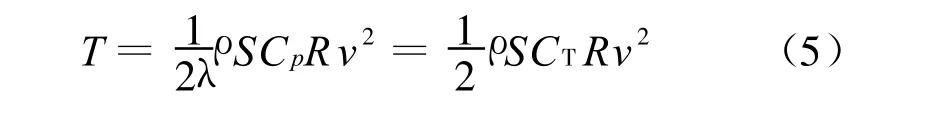
T′e有不同的選擇方式,為了簡化模型又能夠得到較好的系統特性,T′e由發電機額定轉矩折算得到.

建立風力機變槳系統模型后,設計槳距角控制器對風力機輸出功率進行控制,考察其控制性能.

3 單神經元PID自適應槳距角控制系統建模

3.1 系統組成

當風速高于風力發電機的額定風速后,由于風力機結構剛度和材料對載荷的承受極限要求,需要對風力機輸出功率進行控制.通常采用改變風力機槳距角的方式將輸出功率限制在額定值.在控制過程中,對風力機實時輸出功率進行檢測,當實際功率高于額定功率值時,將偏差作為控制輸入,經過PID調節,控制器輸出作為電機驅動器的輸入,變距機構中的伺服電機根據電機驅動器的輸出將槳距角精確定位,使經過調節后的風力機輸出功率等于額定值.槳距角控制框圖見圖2.

圖2 槳距角控制框圖Fig.2 Block diagram of the pitch angle control

3.2 單神經元數學模型

風力機的工況眾多、環境復雜、系統的非線性等造成風力機系統控制的難度.常規PID控制器參數不易調整,缺乏對風力機動態特性及風況變化的自適應能力.為解決這一難題,將單神經元自適應控制方法應用到PID參數的調節中,實現PID參數的在線調節.單神經元數學模型見圖3.其中:x1,x2,…,xi為神經元輸入;w1,w2,…,wi為神經元對x1,x2,…,xi的權系數(即權重值);u為神經元輸出;K為神經元比例系數,K＞0;i為神經元輸入狀態的維數,當i=3時,即為單神經元數學模型[12].

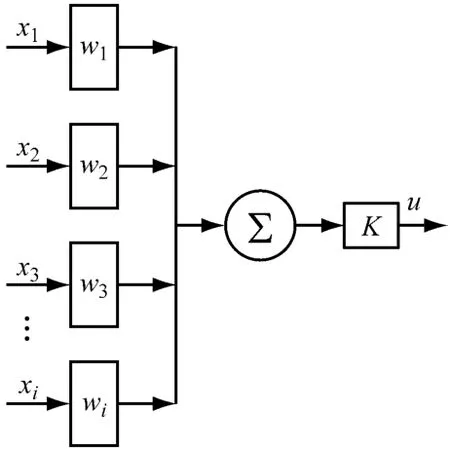
圖3 單神經元數學模型Fig.3 Mathematical model of the single neuron

3.3 單神經元自適應PID控制器

單神經元自適應控制器通過對加權系數的調整來實現自適應、自組織功能,權系數的調整可以選擇相應的學習規則實現.變槳系統單神經元自適應PID控制器的結構見圖4.

圖4 變槳系統單神經元自適應PID控制器結構框圖Fig.4 Block diagram of the single neuron adaptive PID controller for pitch system

單神經元自適應PID 控制算法為[ 13] :

其中:

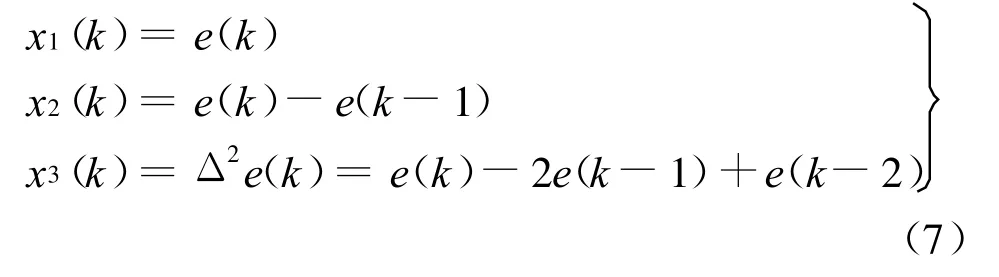
式中:ηI、ηP、ηD分別為積分、比例、微分的學習速率;e(k)為偏差;u(k)為控制對象輸出.

對積分、比例和微分分別采用了不同的學習速率 ηI、ηP和 ηD,以便對不同的權系數分別進行調整.ηP較小時系統較穩定,快速性較好;ηP過大時,系統的快速性雖然變好,但調節時間變長;ηI取適當的值可以使系統獲得較好的快速性.

在控制過程中,單神經元自適應PID控制器通過學習算法不斷在線調節加權系數,使系統能夠適應被控對象的狀態變化.

此處采用有監督的Hebb學習算法,考慮到加權系數w i(k)與神經元的輸入、輸出和偏差有關,其權值的修正公式為[13]:

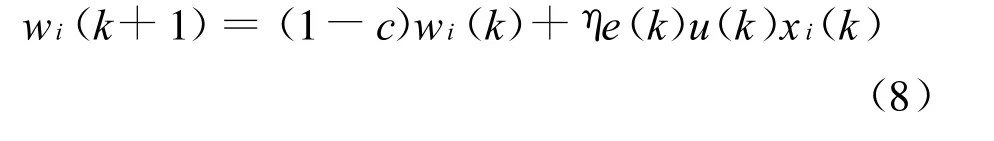
式中:c為常數,0≤c＜1.

通過對偏差信號的檢測,單神經元自適應控制器不斷對實際控制信息進行學習,使控制器的輸出增大或減小.

4 算例仿真

在建立風電系統和單神經元自適應PID控制器的基礎上,對風力機系統在額定風速以上進行功率控制.自然環境狀態下的風速是隨機變化的,規律不易掌握,根據研究的重點是額定風速以上的功率控制,且考慮風速模型的可用性,采用圖5所示的風速圖.

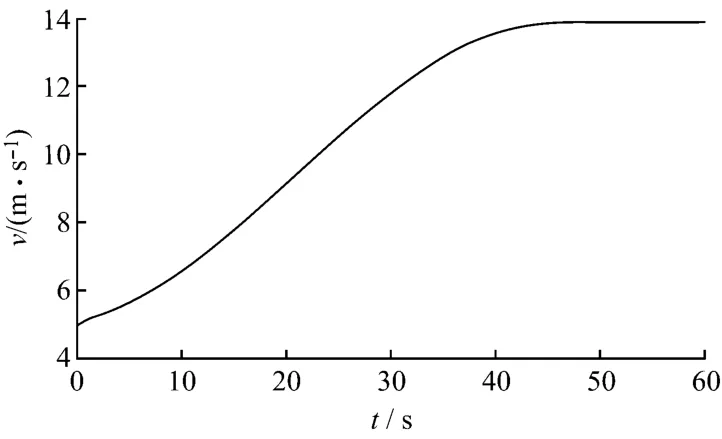
圖5 風速圖Fig.5 Curve of wind velocity

風機系統參數如下:葉片半徑為38.75 m;空氣密度1.225 kg/m3;風機轉動慣量6 027 981 kg·m2;切入風速4 m/s;切出風速25 m/s;額定風速12 m/s;傳動比83;風機額定功率2 MW.系統仿真時間選擇為60 s.在0～60 s間,風速在5～14 m/s變化.風速超過12 m/s后,為保持輸出功率恒定,進行變槳距控制.采用常規PID控制器和單神經元PID控制器進行變槳距控制時,電機輸出轉速見圖6,風電機組輸出功率見圖7.

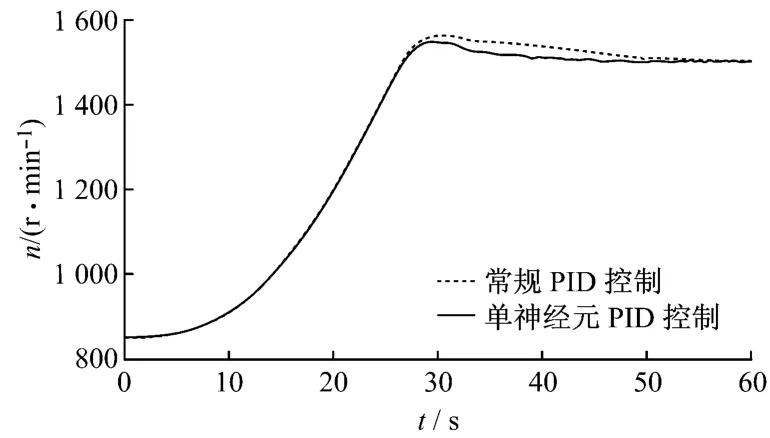
圖6 風電機組電機輸出轉速Fig.6 Output speed of wind turbine generator motor

從圖6可以看出,采用單神經元PID控制器時電機轉速波動更小.

從圖7可以看出,采用單神經元PID控制器進行變槳距控制時,風電機組的輸出功率比采用常規PID控制器進行控制時的性能更優.

圖7 風電機組輸出功率Fig.7 Output power of wind turbine

5 結 論

采用單神經元自適應PID控制器的變槳系統能夠很好地控制槳距角,使風速超過額定值后的輸出功率能夠保持在恒定值.由于單神經元的控制算法過程實質上是參數迭代,因此,與其他非線性控制器相比,這種控制器更易于工程實現并被其他風電系統采用.但是,這種控制器的控制性能也受到采樣數據的影響,采樣數據越多、越精確,則控制器性能越好.同時,在線學習整定參數過程中要確保系統的穩定性,使系統既穩定又能實現有效控制.

[1] WRIGHT A D,FINGERSH L J,BALASM J.Testing state-space controls for the controls advanced rese-ach turbine[C]//The 44thAIAA Aerospace Sciences Meeting and Exhibit.Reno,Nevada:[s.n.],2006:1-18.

[2] JOHNSON K E,PAO L Y,BALAS M J,et al.Control of variable-speed wind turbines standard and adaptive techniques for maxim-izing energy capture[J].IEEE control systems magazine,2006,26(3):70-81.

[3] WRIGHT A D,FINGERSH L J,STOL K A.Designing and testing controls to mitigate tower dynamic loads in the controls advanced research turbine[C]//The 45thAIAA Aerospace Sciences Meeting and Exhibit.Reno,Nevada:[s.n.],2007:1-14.

[4] 耿華,楊耕.基于逆系統方法的變速變槳距風機的槳距角控制[J].清華大學學報:自然科學版,2008,48(7):1221-1224. GENG Hua,YANG Geng.Inverse-system method for pitch control of a variable-speed variable-pitch wind generator[J].J Tsinghua Univ:Sci&Tech,2008,48(7):1221-1224.

[5] CAMBLONG H.Digital robust control of a variable speed pitch regulated wind turbine for above rated wind speeds[J].Control Engineering Practice,2008,16(8):946-958.

[6] BIANCHI F D,MANTZ R J,CHRISTIANSEN C F.Power regulation in pitch-controlled variable speed WECS above rated wind speed[J].Renewerble Energy,2004,29(11):1911-1922.

[7] YILMAZ A S,OZER Z.Pitch angle control in wind turbines above the rated wind speed by multilayer perceptron and radial basis function neural networks[J].Expert System with Applications,2009,36(6):9767-9775.

[8] JAUCH C,ISLAM S M,NSEN P S,et al.Design of a wind turbine pitch angle controller for power system stabilisation[J].Renewable Energy,2007,32(14):2334-2349.

[9] GA LDI V,PICCOLO A,SIANO P.Exploiting maximum energy from variable speed wind power generation systems by using an adaptive Takagi-Sugeno-Kang fuzzy model[J].Energy Conversion and Management,2009,50(2):413-421.

[10] 高峰,徐大平,呂躍剛.大型風力發電機組的前饋模糊-PI變槳距控制[J].動力工程,2008,28(4):537-542. GAO Feng,XU Daping,LüYuegang.Feed forward fuzzy-PI pitch-control for large-scale wind turbines[J].Journal of Power Engineering,2008,28(4):537-542.

[11] 林勇剛.大型風力機變槳距控制技術研究[D].杭州:浙江大學機械與能源工程學院,2005.

[12] 林莘,王德順,徐建源,等.單神經元PID控制器在高壓斷路器運動控制技術中的應用[J].電工技術學報,2009,24(6):35-41. LIN Xin,WANG Deshun,XU Jianyuan,et al.Application of single neuron PID controller in movement control of high voltage circuit breaker[J].Transactions of China Electrotechnical Society,2009,24(6):35-41.

[13] 陶永華,尹怡欣,葛蘆生.新型PID控制及應用[M].北京:機械工業出版社,2002.