基于Matlab和UG的弧齒錐齒輪三維造型技術

劉光磊，田躍軍，樊紅衛，王毛彥

(1．西北工業大學機電學院，陜西 西安 710072;2．第二炮兵駐科工集團型號辦，北京 100830)

1 前言

弧齒錐齒輪傳動平穩、承載能力高、嚙合噪聲小，是現代機械動力系統中傳遞動力和運動的重要部件，在直升機、艦船、汽車、機床和工程機械等工業領域中應用廣泛。

采用ANSYS等有限元軟件分析弧齒錐齒輪的齒面接觸應力、齒根彎曲應力和各種動態應力是研究其強度和振動特性的常用方法。由于弧齒錐齒輪齒面幾何形狀復雜，故通常依據齒輪嚙合原理并采用計算機編程的方法來建立弧齒錐齒輪的齒面數學模型。早期的弧齒錐齒輪設計與分析程序多采用Fortran語言編寫，程序顯得復雜冗長、且顯示功能較弱。Matlab軟件擅長處理數組的各種運算，且圖形顯示功能強大，適合于弧齒錐齒輪的齒面建模過程。借助商用軟件進行齒輪靜動態性能分析時，首先需要把Matlab所建立的齒面模型導入到UG或PRO/E等三維幾何造型軟件中生成弧齒錐齒輪的三維幾何模型，然后再將其導入ANSYS或ABAQUS等有限元軟件中完成應力分析。

利用Matlab生成的弧齒錐齒輪齒面通常是m×n個數據點形式，將其直接導入到UG中后，依然為點陣形式，需要手動逐個選點來生成曲面片，然后通過縫合、陣列和布爾運算等命令來完成實體建模。當齒面網格點數較多時，上述方法顯得繁瑣、費時，且極易出現誤操作。UG/Open GRIP是UG軟件提供的二次開發工具，是UG內嵌的專用圖形交互語言。利用UG/Open GRIP將Matlab得到的齒面離散數據轉換成三維實體模型的過程通過編程來實現，程序自動拾取數據點，并整合了曲面和實體生成的諸多步驟，提高了建模效率和模型的準確性。

2 Matlab中齒面網格數據的生成

弧齒錐齒輪的加工策略決定著齒面幾何形狀。通常，采用展成法或成型法形成大輪的齒面，然后根據嚙合性能要求配切出合理的小輪齒面。在計算機中建立齒面數學模型就是按照上述齒輪加工原理進行的，首先需要建立弧齒錐齒輪副的加工坐標系，包括刀具坐標系、搖臺坐標系、機床坐標系、輔助坐標系和齒輪坐標系等。刀具旋轉表面的基本方程采用雙參數法表示，齒面方程即為刀具旋轉表面方程依次經過如上幾個坐標的轉化后得到［1－4］。齒根過渡曲面方程［5］的建立與之類似，區別僅在于形成過渡曲面的部分是刀尖圓角，而非刀具的直刃部分。當獲得工作齒面和齒根過渡曲面的基本方程后，可以對整個輪齒進行網格劃分，并求得網格節點的三坐標值。

在Matlab中劃分網格時，要顧及UG實體造型對離散數據點的要求。因為UG只能夠處理連續光滑的空間四邊形曲面，無法體現不同曲面片連接處的棱角特征;在每一曲面片中，還要求該曲面上的離散點盡可能均勻或漸變、每行和每列的點數相等。為此，在生成輪齒表面的數據點時，首先將輪齒分為若干曲面片;在每一曲面片中，為了滿足有限元網格劃分時單元形狀不過分畸變的要求，將單一曲面片再劃分為若干子曲邊四邊形。

在Matlab中生成齒面網格點數據的程序流程圖如圖1所示。

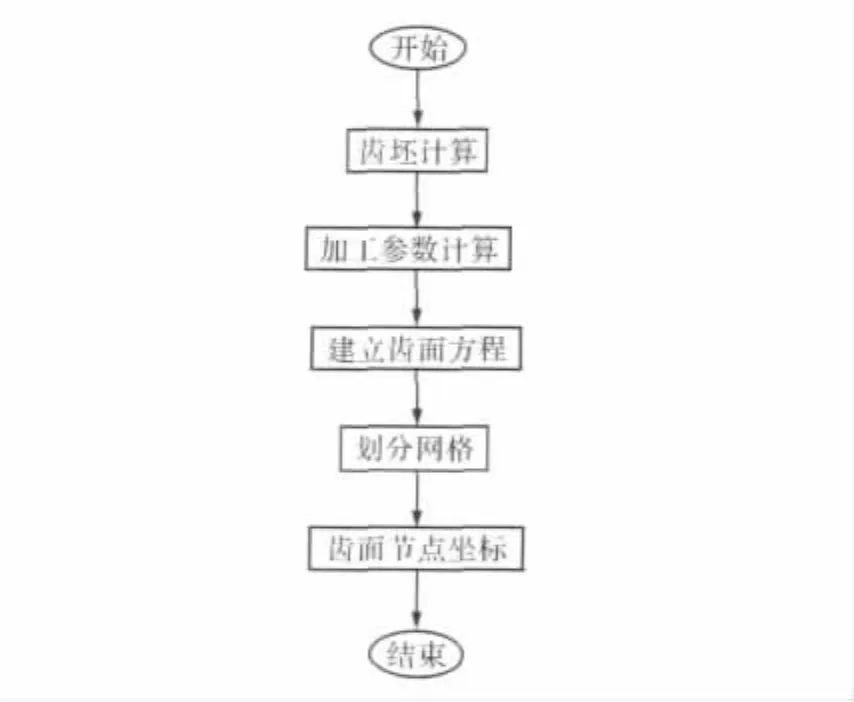
圖1 在Matlab中生成齒面網格點數據流程圖

弧齒錐齒輪齒面網格點的坐標數據是在UG環境下應用二次開發功能重建齒面并構造三維實體模型的關鍵所在。以此數據為基礎建立的弧齒錐齒輪實體模型是精確的。

3 基于UG/Open GRIP的齒輪三維造型［6］

使用UG對Matlab生成的齒面數據點進行三維建模的基本過程為:①齒面生成;②邊界縫合;③實體陣列;④布爾運算。

3.1 GRIP程序的開發過程

GRIP語言具有完整的語法規則、程序結構、內部函數以及和其他語言相互調用的功能。GRIP程序的一般開發過程如下。

(1)編寫GRIP源程序。用Windows自帶的記事本編寫GRIP語言的源程序，存盤時文件的擴展名為.grs;或在UG高級開發環境GRADE中按照“開始—程序—Unigraphics NX—Unigraphics Tools—UG/Open GRIP”進入到UG開發環境中，用Edit功能編寫GRIP源程序，存盤時文件的擴展名同樣為.grs。

(2)編譯GRIP源程序。在UG的高級開發環境GRADE中，用Compile功能編譯文件擴展名為.grs的GRIP源程序，編譯成功后生成擴展名為.gri目標文件。

(3)鏈接目標文件。用Link功能鏈接擴展名為.gri的目標文件，鏈接成功后生成擴展名為.grx的可執行文件。

(4)執行可執行文件。執行程序時必須先進入UG環境中。為此，在UG界面下選擇“File—Execute UG/Open—Grip”，在彈出的“執行GRIP程序”的對話框中，選擇要執行的.grx文件。

3.2 B樣條插值齒面的生成

UG/Open GRIP生成曲面的方法共有六種，即點方法、曲線組方法、二次曲面法、曲線網格法、掃掠面生成法和轉換法。

基于Matlab齒面離散點在UG/Open GRIP中生成曲面時，只能采用點方法。B曲面的點建模方法分為曲面通過點和點作為曲面的控制頂點兩種。由于重構的目標齒面要求用數值齒面數據點來重構才能達到精確建模，因此，重構出的曲面要嚴格通過各數據點，這種方法為插值法。通過插值法可以由內部程序自動生成小曲面。

UG/Open GRIP內部點方法生成B曲面的具體操作步驟為:①在Matlab中生成矩陣形式的數據點;②獲取數據點數和行列數，并設定曲面類型;③逐行逐個按序拾取數據點;④生成B曲面。

3.3 曲面的縫合

通過插值法生成的小曲面之間雖然邊界數據共用，但生成的各小曲面之間并不是光滑連續的，需要對小曲面邊界進行修補和縫合。從圖2、3可以清楚地看到Matlab齒面網格劃分為六大塊、二十小片。使用邊界縫合生成單個輪齒完整齒面，進而生成實體。這既保證了邊界處的連續性又直接生成了其他商用分析軟件可識別的實體。

3.4 輪齒實體的陣列和布爾運算

以上一步生成的單個輪齒實體為操作對象，用已知的對稱軸、旋轉角度得到相應的變換矩陣，實體陣列并進行布爾運算后，可以得到精確的含過渡曲面的弧齒錐齒輪大、小輪的三維幾何模型。

4 算例

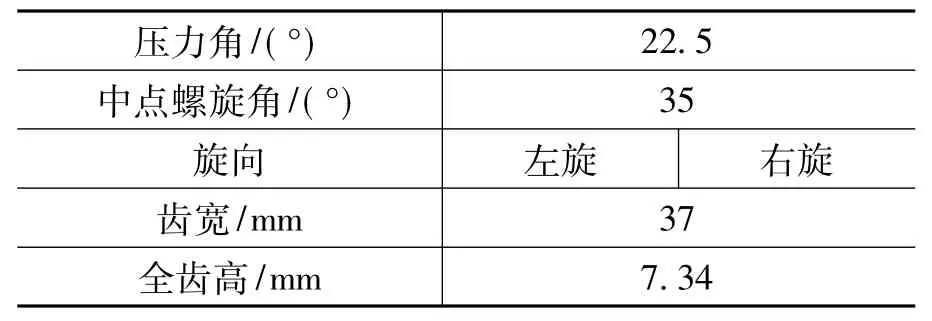
針對表1所列某航空發動機附件傳動弧齒錐齒輪，采用本文的方法建立弧齒錐齒輪的三維實體模型。圖2～圖8為所建立Matlab齒面網格顯示和對應的UG弧齒錐齒輪大小齒輪的單齒、全齒和嚙合模型。

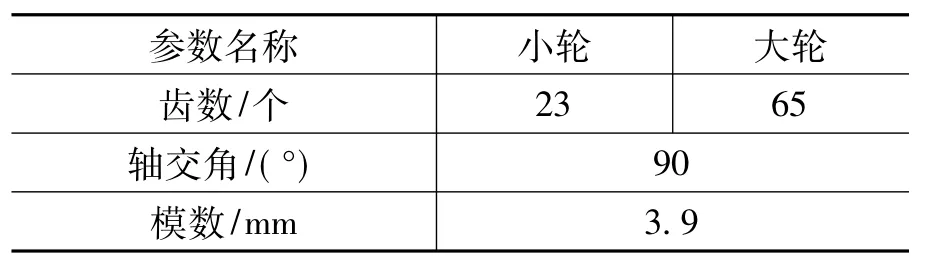
表1 弧齒錐齒輪基本參數

5 結論

討論了在Matlab中生成弧齒錐齒輪齒面的基本過程，借助UG二次開發功能將從Matlab仿真得來的齒面數據點陣，運用B樣條插值的方法生成了弧齒錐齒輪的齒面，并對該齒面進行縫合、陣列和布爾運算，最終實現對Matlab中離散齒面的UG重構和三維建模。

編程實踐表明，本文提出的方法可以快速有效地實現離散曲面在UG軟件平臺中的精確造型，進而利用UG提供的數據輸出功能將模型輸出到其它CAE軟件中，為弧齒錐齒輪的有限元分析提供良好的基礎。

［1］ Litvin F L，Zhang Yi．Local synthesis and tooth contact analysis of face-milled spiral bevel gears［R］．NASA CR-4342， AVSCOM TR-90-C-028， NASA Office of Management Scientific and Technical Information Division，1991．

［2］ Litvin F L，Wang A G，Handschuh R F．Computerized generation and simulation of meshing and contact of spiral bevel gears with improved geometry［J］．Computer methods in applied mechanics and engineering．1998，(158):35 －64．

［3］ Argyris John，Fuentes Alfonso，Litvin F L．Computerized integrated approach for design and stress analysis of spiral bevel gears［J］．Computer methods in applied mechanics and engineering，2002，(19):1057－1095．

［4］ Litvin F L，Fuentes Alfonso，Mullins Baxter R，et al．Computerized design，generation，simulation of meshing and contact，and stress analysis of formate cut spiral bevel gear drives［R］．NASA/CR-2001-210894，ARL-CR-467，National Technical Information Service，2003．

［5］ Litvin F L，Fuentes Alfonso，Hayasaka．Design，manufacture，stress analysis，and experimental tests of lownoise high endurance spiral bevel gears［J］．Mechanism and Machine Theory．2006，(41):83 －118．

［6］ 夏天，吳立軍．UG二次開發技術基礎［M］．北京:電子工業出版社，2005．