基于高斯過程的精密衛星鐘差加密

劉 冬,張清華,2

1.西安測繪研究所,陜西西安 710054;2.信息工程大學測繪學院,河南鄭州450052

基于高斯過程的精密衛星鐘差加密

劉 冬1,張清華1,2

1.西安測繪研究所,陜西西安 710054;2.信息工程大學測繪學院,河南鄭州450052

將高斯過程方法應用到精密衛星鐘差加密中,通過選擇合適的核函數,將5 min間隔的鐘差數據插值到30 s間隔。將結果與IGS提供的30 s精密鐘差數據和四階多項式擬合插值方法得到的結果進行比較,結果表明,高斯過程方法具有較高的加密精度,適用于 GPS所有在軌衛星的原子鐘鐘差的加密,達到厘米級精度。

精密鐘差;加密;高斯過程;回歸

1 引 言

GPS精密單點定位技術不能用組差的方式來消除衛星鐘差,而廣播星歷中的衛星鐘差精度也僅為7 ns,無法滿足精密單點定位的要求。通常采用IGS提供的鐘差產品,將15 min或5 min的精密衛星鐘差加密到用戶所需的采樣間隔。由于實際數據采樣率會更高,所以必須采用估計或內插的方法得到高采樣率的衛星鐘差。因此,對精密星歷進行內插或擬合就成為 GPS精密數據處理等實際應用中的重要工作。

目前,國內外較常用的加密方法是Lagrange多項式插值、Newton多項式插值、Hermite插值、樣條函數插值、切比雪夫多項式插值、三角函數插值等[1-2]。

本文采用高斯過程回歸方法進行精密鐘差加密,通過選擇合適的協方差函數,將 IGS提供的5 min間隔的精密鐘差數據插值到30 s間隔,試驗結果表明,該方法具有較高的加密精度,且對所有的衛星原子鐘都有較強的適用性。

2 高斯過程回歸

高斯過程回歸是近年來由統計學理論發展來的一種全新學習機,它將函數視為變量,由訓練數據和貝葉斯估計理論得到關于函數的后驗概率估計,達到對函數學習的目的。它對處理高維數、非線性復雜分類和回歸問題具有很好的適應性,且泛化能力強,與人工神經網絡、支持向量機相比,有較容易實現的特點。

2.1 高斯過程

隨機過程可以定義為在某個概率空間上的一簇隨機變量。高斯過程是一種重要的隨機過程,是對高斯分布的推廣。如果高斯分布是描述向量的分布情況,那么可以將高斯過程理解為是描述函數的分布情況。

高斯過程又稱正態隨機過程,其任意有限變量集合都有著聯合高斯分布的特性,即對于任意整數 n≥1及任意的變量 x1,x2,x3,…,xn,與其對應的函數 f(x1),f(x2),f(x3),…,f(xn)的聯合概率分布服從n維高斯分布。高斯過程的全部統計特征完全由它的均值 m(x)和核函數 k(x,x′)來確定,一般記為 f(x)～GPf(m(x),k(x,x′))。核函數是任意一對輸入的隨機變量 x和 x′的協方差函數。高斯過程的核函數必須是半正函數。與神經網絡類似,通常需要通過訓練數據集來確定核函數的超參數,具體訓練方法見參考文獻[3—4]。

假設有 N個觀測數據的訓練集D={(x1,y1),(x2,y2),(x3,y3),…,(xN,yN)},xi∈Rnx,是nx維輸入矢量,yi∈R是相應的輸出標量,令 X=[x1x2x3… xN],y=[y1y2y3…yN]。應用內積空間中的重構核希爾伯特空間(reproducing kernel Hilbert space,RKHS)來描述輸入輸出的關系,即考慮映射 φ:Rnx|→H,由此可得

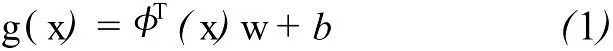
一般情況下,認為 b=0(可以采用剔除均值的方法得到)。對于給定的訓練數據集

如果假定w的先驗概率為N(0,I),其中ε是獨立的隨機變量,服從均值為0,方差為δ2εI的高斯分布,那么 y是高斯過程。

令 k(xi,xj)=〈φ(xi),φ(xj)〉,則

式中,Kij=k(xi,xj)。

2.2 高斯過程預測

高斯過程預測是指對任意的測試輸入 x＊,給出其函數值的預測值 g(x＊),寫成概率分布函數的形式,即條件分布p(g(x＊)|x＊,X,y)。根據公式(3)可以將訓練輸出 y和預測值g(x＊)寫成聯合分布,即

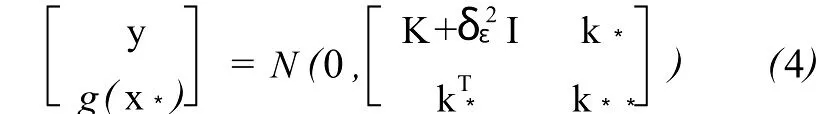
式中,k＊=K(X,x＊),k＊＊=k(x＊,x＊)。根據聯合分布,可以很容易得到 g(x＊)的條件分布函數

3 基于高斯過程的鐘差加密

導航衛星中在外部空間受到極其復雜的環境影響,使得鐘差數據具有一定的不穩定性,又沒有具體的規律可循,因此可以通過高斯過程回歸的學習能力對鐘差數據來進行擬合,進而進行加密。在學習過程中,協方差函數的選擇非常重要。

在考慮時變鐘漂參數時,國外常用的頻漂模型是對數模型和指數模型。同時在對 GPS衛星鐘特性分析和實際鐘差數據試驗的基礎上,選取Matern協方差函數作為核函數[3],其表達式如下

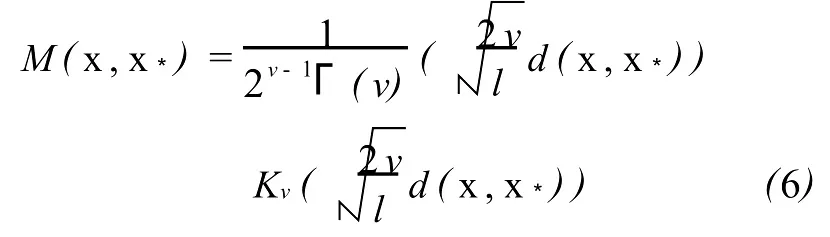
式中,v,l是正參數;Kv(·)為修正的Bessel函數;d(x,x＊)為距離函數。在實際應用中,核函數的參數選擇為v=3/2,l=1。選擇了各向同性函數作為距離函數,即

式中,p為比例系數。最終采用的核函數為

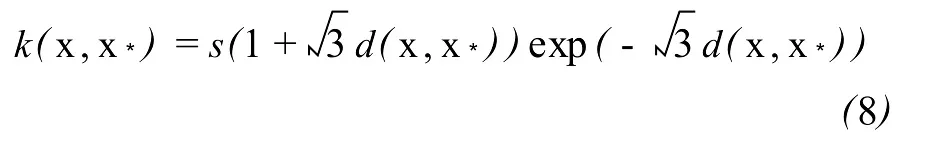
式中,s為信號方差,s和p是該核函數的超參數。如果將距離當作變量,顯然,該核函數可以看成是一個指數函數和一階多項式的乘積。

4 算例與分析

為了分析與比較幾種鐘差加密方法的精度,采用IGS提供的2009-08-21的間隔為30 s的鐘差數據(igs15455.clk_30s)。在其中讀取衛星的鐘差,其采樣間隔為30 s,將其作為真值,再從中挑選間隔為5 min的數據作為節點,分別用多項式擬合法(Polyfit),高斯過程回歸算法(GP)進行加密,并將加密結果與真值進行比較分析,其方案如下:

(1)用四階多項式擬合和高斯過程回歸算法來對 PRN32衛星在一天內的數據進行加密,并對加密的結果進行統計分析。

(2)采用四階多項式和高斯過程回歸算法對不同類型的衛星原子鐘的鐘差加密進行加密,對結果進行統計分析。

4.1 PRN32衛星的鐘差加密

采用四階多項式和高斯過程方法對PRN32衛星鐘差進行加密,其24小時的擬合結果如圖1所示,圖2給出了局部放大的擬合結果,圖3是鐘差擬合殘差(與真實鐘差的差),每個歷元為30 s。由圖3可以看出,采用 GP方法得到的精密鐘差與真實鐘差的偏差非常小,并且在24小時中都非常穩定,而采用四階多項式方法得到的鐘差不僅加密誤差加大,而且具有明顯震蕩。表1給出采用不同方法得到的擬合均方誤差(RMS),顯然,采用 GP方法進行鐘差加密要比四階多項式方法鐘差加密的精度提高很多(相差一個數量級),達到了27 ps,等效距離誤差約0.81 cm。

圖1 鐘差擬合結果曲線(PRN32衛星)Fig.1 Clock error fitting(PRN32)

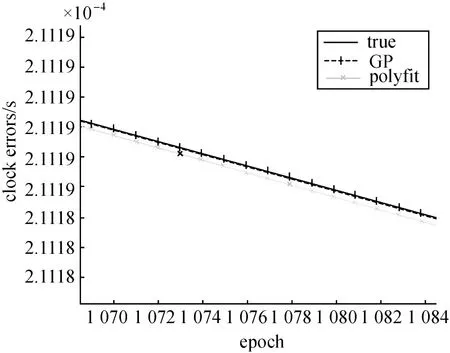
圖2 鐘差擬合結果局部放大曲線(PRN32衛星)Fig.2 Clock error fitting selective enlargement(PRN32)

表1 加密精度比較(PRN02衛星)Tab.1 Comparison of densification precision(PRN32)/ns

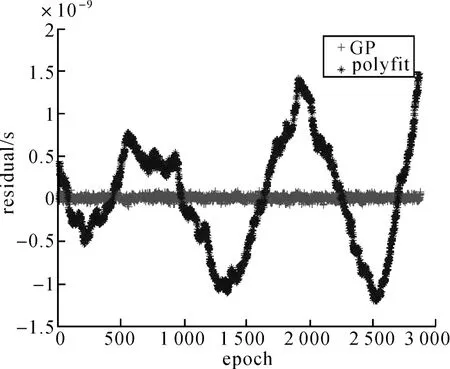
圖3 鐘差擬合殘差曲線(PRN32衛星)Fig.3 Clock error fitting residual(PRN32)

4.2 不同類型衛星鐘的鐘差加密

為了驗證 GP方法鐘差加密的適用性,利用IGS提供的2009-08-21所有衛星鐘差數據進行試驗。圖4是采用四階多項式方法對不同衛星鐘中進行鐘差加密精度(均方誤差)。圖5是采用GP方法對不同衛星鐘中進行鐘差加密精度(均方誤差)。表2是兩種方法對不同衛星鐘加密精度的統計結果。通過對比,采用 GP方法對不同衛星鐘的鐘差進行加密,都可以得到較高的插值精度,且不同衛星鐘的擬合誤差量級基本相同;四階多項式方法對 GPS中BlockⅡA衛星的Cs鐘的擬合誤差較大。分析結果表明:采用四階多項式方法加密鐘差,對于 GPS中BlockⅡA衛星的Cs鐘和Rb鐘,鐘差誤差達到了分米級;GP方法對于所有的 GPS衛星鐘加密都有非常好的適用性,加密精度都可達到厘米級。

圖4 多項式擬合的加密精度Fig.4 Densification precision of polynomial fitting

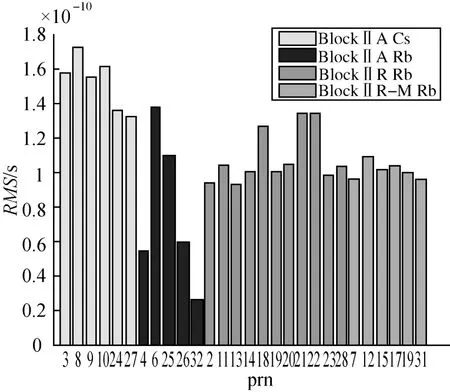
圖5 高斯過程回歸加密精度Fig.5 Densification precision of Gaussian processregression

表2 不同衛星原子鐘加密精度比較Tab.2 Comparison of densification precision for different satellite atomic clocks /ns

5 結束語

鐘差加密是 GPS數據處理中重要而經常性的工作,應用高斯過程方法對 GPS衛星鐘的鐘差進行加密,通過與四階多項式鐘差加密方法的精度對比,得出以下結論:①采用 GP方法對 GPS衛星鐘的鐘差進行加密具有較高的插值精度高,殘差穩定;②GP方法鐘差加密對于所有的 GPS衛星鐘都有普遍的適用性。

[1] HAN Baomin.Densification Methods of GPS Satellite Clock Errors and Their Impact on Orbit Determination Precision of LEOs[J].Geomatics and Information Science of Wuhan University,2006,31(12):1076-1079.(韓保民.精密衛星鐘差加密方法及其對星載 GPS低軌衛星定軌精度影響[J].武漢大學學報:信息科學版,2006,31(12):1076-1079.)

[2] HONG Ying,OU Jikun,PENG Bibo.Three Interpolation Methods for Precise Ephemeris and Clock Offset of GPS Satellite[J].Geomatics and Information Science of Wuhan University,2006,31(6):516-518.(洪櫻,歐吉坤,彭碧波.GPS衛星精密星歷和鐘差三種內插方法的比較[J].武漢大學學報:信息科學版,2006,31(6):516-518.)

[3] RASMUSSEN C E,WILLIAMS C K I.Gaussian Processes for Machine Learning[M].Berlin:Springer,2006.

[4] RASMUSSEN C.Evaluation of Gaussian Processes and Other Methods for Non-linear Regression[D].Toronto:University of Toronto,1996.

(責任編輯:宋啟凡)

Densification of Precise Satellite Clock Errors Based on Gaussian Processes

LIU Dong1,ZHANG Qinghua1,2
1.Xi’an Institute of Surveying and Mapping,Xi’an 710054,China;2.Institute of Surveying and Mapping,Information and Engineer U-niversity,Zhengzhou 450052,China

The Gaussian processes(GP)method is used to densify the 5 min interval clock errors to 30 s interval with a suitable kernel function.The densification results are compared with the IGS data and the densified clock errors using the four order polynomial interpolation method.The results indicate that the GP method can provide high densification precision and is applicable to densify the clock errors of all GPS on-board atom clocks.The accuracy is up to the centimeter level.

precise clock errors;densification;Gaussian processes;regression

LIU Dong(1977—),male,PhD,majors in is satellite navigation and nonlinear signal processing.

P135

:A

1001-1595(2011)S-0059-04

2011-01-31

修回日期:2011-03-19

劉冬(1977—),男,博士,研究方向為衛星導航與非線性信號處理。

E-mail:ld_yzy@yahoo.com.cn