地球靜止軌道衛星廣播星歷參數擬合與試驗分析

何 峰,王 剛,劉 利,陳劉成,胡小工,黃 勇,宋葉志,阮仁桂

1.北京環球信息應用開發中心,北京100094;2.中國科學院上海天文臺,上海200030;3.西安測繪研究所,陜西西安710054

地球靜止軌道衛星廣播星歷參數擬合與試驗分析

何 峰1,2,王 剛1,劉 利1,陳劉成1,胡小工2,黃 勇2,宋葉志2,阮仁桂3

1.北京環球信息應用開發中心,北京100094;2.中國科學院上海天文臺,上海200030;3.西安測繪研究所,陜西西安710054

介紹 GEO衛星廣播星歷參數超限的現象和規律,根據解算方程病態性和軌道動力學特性分析該參數超限的原因,設計在不顯著損失精度前提下多種改善參數超限的擬合方案,利用實測數據進行試驗。結果表明:固定超限參數的同時解算其余星歷參數和進行參數嶺估計的方法,都能夠有效地抑制并解決參數超限問題。

地球靜止軌道;星歷擬合;相關性;嶺估計

1 引 言

廣播星歷參數是衛星導航電文的主要內容之一,它的選擇和設計不僅決定了廣播星歷所能達到的精度,而且還決定了用戶算法的復雜程度。廣播星歷參數的選擇和設計,以及精度和外推能力是影響導航系統可靠性和地面控制復雜程度的重要因素。廣播星歷是對精密星歷的近似或逼近,一般可通過近似的分析解或者數值擬合得到,它的精度除受精密星歷本身的精度制約外,在很大程度上和廣播星歷參數的選擇,采用的導航參數設計算法以及用戶算法的精度有關。現有的衛星導航系統中,GPS和 GLONASS采用不同的參數表達形式[1],兩種星歷參數表達方式的特點如表1所示。

我國的區域衛星導航系統Compass向用戶發播的導航電文采用了與 GPS相同的參數化方案。其中,廣播星歷利用考慮一階攝動影響的15個軌道根數描述衛星軌道,同時利用二階多項式的3個參數描述衛星的鐘差預報。與 GPS系統采用全星座MEO衛星不同,Compass系統采用GEO+ISGO+MEO三種衛星的混合星座,其中 GEO衛星在軌道特性方面具有高軌道、小傾角的特點,與MEO衛星相比存在較大差異,因此沿用 GPS的廣播星歷參數描述GEO衛星存在潛在的不適應性。

表1 GPS和 G LONASS的廣播星歷參數和性能特點Tab.1 Ephemeris characteristics of GPS and G LONASS

針對導航廣播星歷擬合計算方法,已有大量的研究工作,包括廣播星歷用戶算法的有效性、參數估計方法和高軌小傾角衛星擬合算法等[2-5],這些算法解決了不同類型衛星星歷擬合的成功率和擬合精度問題。然而,實際系統組網運行過程中發現在克服精度損失問題后,在特定時段,GEO廣播星歷部分參數在編碼導航電文時超過了系統設計分配給該參數的比特位限制,即參數超限。在同樣的算法條件下,IGSO衛星未發現星歷超限現象。針對上述問題,首先介紹不同類型衛星進行星歷參數擬合過程中超限參數Δn的變化規律,詳細分析 GEO衛星星歷擬合中參數超過接口范圍的數學和動力學原因,設計了抑制Δn超限的算法,并通過實測數據對算法有效性進行驗證,解決星歷參數超限問題。

2 星歷擬合中參數變化特性與原因分析

2.1 參數變化特性分析

衛星廣播星歷15個參數中,Δn主要描述衛星軌道運動平均角速度的修正項。為了分析參數Δn的變化特性,分別利用不同軌位的在軌衛星2010年6月、10月和12月中實際測定軌數據對星歷參數進行擬合,得到參數Δn的變化曲線如圖1～圖4所示(圖1～圖3中橫線為接口設定門限)。

圖1 2010-06月 GEO-A擬合Δn曲線Fig.1 Δn fitting result of GEO-A in 2010-06

圖2 2010-12月 GEO-A擬合Δn曲線Fig.2 Δn fitting result of GEO-A in 2010-12

圖3 2010-10月 GEO-B擬合Δn曲線Fig.3 Δn fitting result of GEO-B in 2010-10

圖4 2010-10月IGSO-A擬合Δn曲線Fig.4 Δn fitting result of IGSO-A in 2010-10

從不同衛星星歷擬合參數一個月中Δn長期變化曲線來看,Δn值存在以1 d為周期的變化,每日峰值則存在約15 d為周期的近似正弦變化,峰值超過接口規定范圍的時段,即出現參數超限現象。從圖中結果可以看出,對于 GEO-A衛星,6月和12月均存在兩個階段Δn值達到峰值并超過接口規定范圍,GEO-B衛星也有相似現象,而IGSO-A衛星則未發現星歷參數超限現象,經計算發現其余月份也有類似結果。

2.2 參數相關性分析

GEO衛星存在高軌道、小傾角等特點,星歷擬合中盡管采用了參考坐標面小角度旋轉的策略,保證擬合的成功率[4-5],但仍然無法從根本上完全避免擬合方程的病態性。為了驗證實測數據條件下方程的病態程度,采用2010年6月和10月不同衛星實際定軌數據對星歷參數間的相關性進行分析。不同類型衛星擬合時,參數Δn與其余14參數相關性如表2所示。

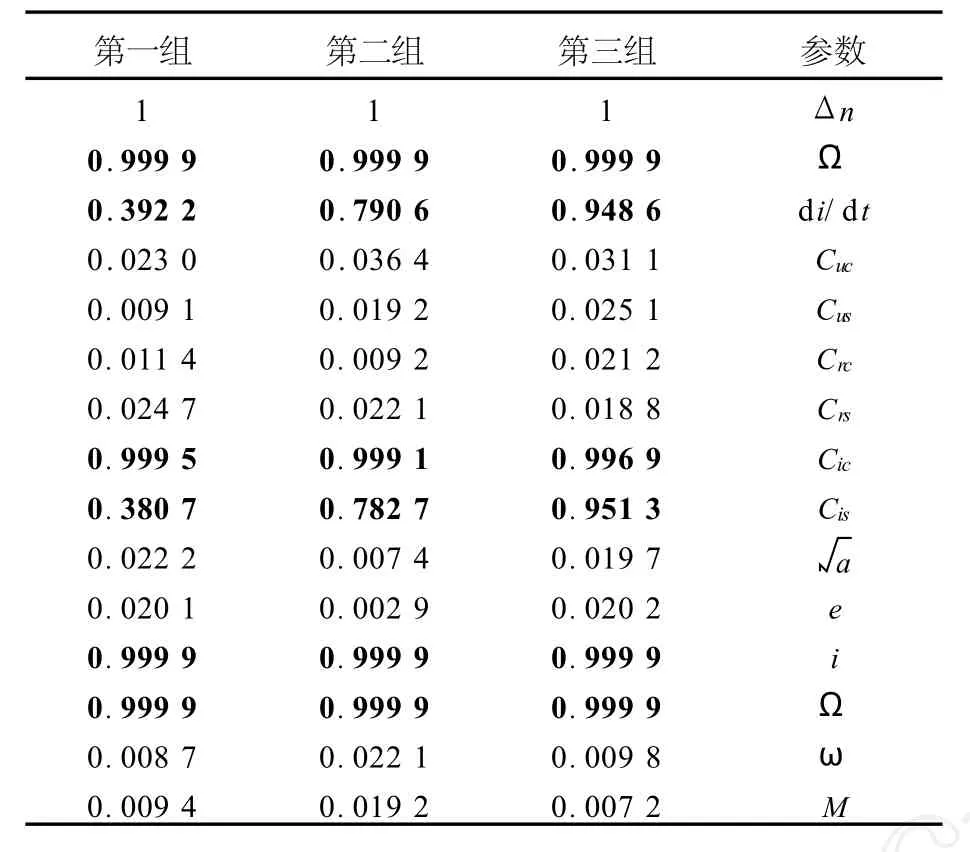
表2 GEO-A衛星擬合時Δn與其余14個參數的相關系數表Tab.2 Correlation coefficient betweenΔnand others of GEO-A

表3 IGSO-A衛星擬合時Δn與其余14個參數的相關系數表Tab.3 Correlation coefficient betweenΔnand others of IGSO-A

從計算結果來看,參數Δn與Ω、di/dt、Cic、Cis、i、Ω具有較強的相關性,這是導致方程病態的一個重要原因。對于 GEO衛星,與Δn相關系數超過0.99的參數有4個,而對于 IGSO衛星來說,則無任何參數與Δn相關系數大于0.99。這也說明,IGSO衛星擬合時Δn與其他參數的相關性相對較小,法方程病態程度相對較弱。

不同定軌時段 GEO衛星15個參數之間的相關系數如圖5、圖6所示。

圖5 2010-06-02日參數間相關系數Fig.5 Correlation coefficient between all parameters in 2010-06-02

圖6 2010-06-12日參數間相關系數Fig.6 Correlation coefficient between all parameters in 2010-06-12

從圖中結果可以看出,對于 GEO衛星,15個參數之間均存在較強的相關性,多數參數之間的相關系統接近1,擬合方程病態程度較強,這使得方程求解時部分參數偏離其真實值存在一定的可能性。

2.3 Δn參數近似值計算

從廣播星歷參數相關性分析可知,星歷擬合方程的病態性導致參數解算結果偏離其真實值存在一定的可能。為了驗證參數實際解算值偏離其真實值的程度,采用數值方法對參數Δn的近似值進行計算,通過對近似值進行分析,判斷擬合值在數值量級上偏離其真實值的程度。

用戶使用的廣播星歷用戶算法中,在某組星歷有效期的1 h內有

星歷擬合時,采用4 h軌道數據進行參數擬合,得到包括Δn在內的15個參數。在此,為了計算Δn的近似值,取4 h中每5 min一個歷元的軌道結果(共48個值),分別計算對應時刻的角速度值ni,由于所取點時間間隔較小,4 h內點密度足夠大,可以將4 h內角速度平均值近似等價于平均角速度,再由Δn=-ntoe,可得Δn 的近似值。基于上述原理,利用不同衛星實際定軌數據計算Δn近似值如圖7、圖8所示。

圖7 2010-06月 GEO-A計算Δn近似值Fig.7 ApproximateΔnvalue of GEO-A in 2010-06

圖8 2010-10月—11月IGSO-A計算Δn近似值Fig.8 ApproximateΔnvalue of IGSO-A in 2010-10 and 2010-11

對不同衛星的擬合結果和計算近似值進行比較,結果如表4所示。

從兩顆衛星的近似值計算結果來看,Δn的計算值與實際擬合值在峰值曲線變化上均呈現一定的一致性,但對于 GEO衛星,計算結果與擬合結果相差一個量級,對于IGSO衛星,計算結果峰值量級與實際擬合結果基本一致,這也從另一方面說明與GEO衛星相比,IGSO衛星擬合法方程病態程度較輕。

表4 不同衛星Δn計算值與擬合值的比較Tab.4 Contrast between computing value and fitting value of Δn for different satellite

2.4 攝動影響分析

分析GEO衛星參數Δn的曲線圖可以看出(如圖9、圖10),Δn的變化除周日周期以外,每日峰值呈現近半月周期變化,考慮衛星受攝運動所有周期特性,推測可能與月球第三體攝動相關。與MEO衛星相比,高軌 GEO衛星受到的月球三體攝動超過MEO衛星,因而 GEO軌道一階攝動解的相應項量級大于MEO的相應攝動量級,進一步分析6月和12月兩個月中的Δn變化規律可以發現其中一個峰值從6月的12日提前到12月的6日(如圖9、圖10),峰值變化為6 d,這正好與月球攝動28 d的周期相吻合。

圖9 2010-06月 GEO-A擬合Δn曲線Fig.9 Δn fitting result of GEO-A in 2010-06

為了進一步驗證月球攝動的影響,利用實際定軌得到的 GEO衛星和IGSO衛星的初始軌道和動力學參數,在不考慮月球攝動的條件下分別積分軌道,利用積分軌道擬合廣播星歷參數,對得到的參數Δn進行分析。參數Δn擬合結果如圖11、圖12所示,從圖中可以看出,忽略月球攝動之后,兩種衛星的Δn值變化曲線完全消除峰值的半月周期變化,擬合得到的峰值只存在小幅度的近似線性變化,這說明月球攝動是Δn參數擬合值每日峰值出現近似半月周期變化的主要原因之一。

圖10 2010-12月 GEO-A擬合Δn曲線Fig.10 Δn fitting result of GEO-A in 2010-12

圖11 未考慮月球攝動時 GEO-A擬合Δn曲線Fig.11 Δn fitting result of ignoring lunar perturbation

圖12 未考慮月球攝動時IGSO-A擬合Δn曲線Fig.12 Δn fitting result of ignoring lunar perturbation

綜合上述分析可以看出,對于Δn與其余參數相關性較強的 GEO衛星,Δn的擬合值峰值遠大于計算的近似值,而對于Δn與其余參數相關性相對較弱的IGSO衛星,Δn的擬合值峰值與計算的近似值基本一致,其中Δn近半月峰值周期變化是由于月球第三體攝動引起,因此可以認為GEO衛星解算得到的Δn值中既包含了軌道的攝動周期特性,又吸收了由于方程嚴重病態導致的其他誤差,Δn嚴重偏離其理論值并造成超出接口范圍的原因是星歷參數之間強相關性與軌道攝動之間復雜的綜合結果。

3 參數超限抑制算法與驗證

3.1 固定Δn解算其余14個參數的算法

從前面的參數相關性分析中可以看出,對于GEO衛星來說,進行星歷擬合過程中,Δn與其余參數存在較強的相關性,在此,為了降低方程求解時的相關性,采用將Δn固定的方式,求解其余14個參數的方法,Δn的值取為與門限接近的3.999e-9。基于以上算法原理,對6月份5個不同時段的定軌文件進行星歷擬合試驗,擬合得到超限星歷組數統計如表5所示。

表5 超限星歷組數統計表Tab.5 Statistics of over-limitation ephemeris

從擬合結果看出,固定Δn條件下擬合其余14個參數,出現參數 e和di/dt超限的現象,說明采用固定Δn+固定擬合弧長的方法無法完全解決參數超限問題。

在計算結果不滿足要求的條件下采用調整擬合數據弧長的策略,對2010-06月定軌數據重新進行星歷擬合計算,結果如表6所示。

表6 超限星歷組數統計表Tab.6 Statistics of over-limitation ephemeris

從表中數據可以看出,通過固定Δn值的同時調整擬合數據弧段長度,在4 h數據擬合超限時調整數據弧段為5 h或3 h。6月份5個時段定軌文件擬合的星歷中,Δn超限的組數均有明顯的減少,一個月中超限星歷組數減少到2組,可見上述方法對于抑制Δn超限的現象具有明顯的效果。

3.2 有偏估計算法

有偏估計是解決方程病態性問題的方法之一,針對 GEO衛星星歷擬合的方程病態問題,采用有偏估計的方式降低方程的病態性,壓縮待估計參數的模,在保證擬合誤差的前提條件下,將參數控制在接口范圍門限以內。

具體策略是當Δn參數超限后,對Δn進行參數嶺估計,考慮到工程的實際需求,嶺參數確定的原則并不以最優為準則,而只要滿足擬合結果要求即可。基于此策略對6月份的 GEO-A衛星定軌結果進行星歷擬合試驗,結果如下。

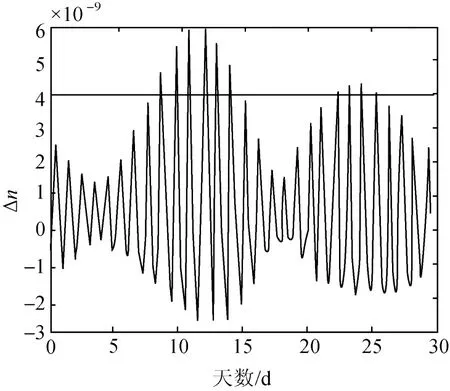
圖13 未進行參數嶺估計條件下的Δn曲線Fig.13 Δn fitting result without ridge estimate

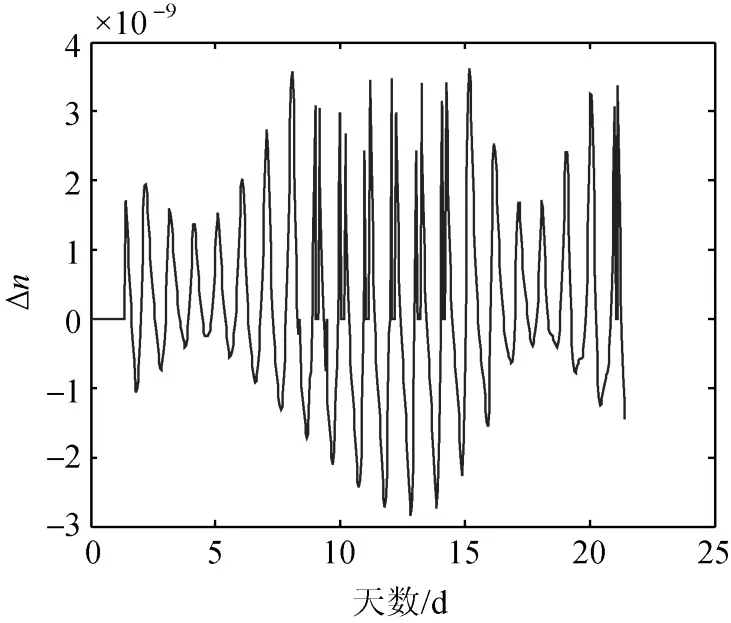
圖14 參數嶺估計條件下的Δn曲線Fig.14 Δn fitting result with ridge estimate

從6月份的數據看來,在擬合的Δn參數超限后通過嶺估計的方法,將Δn值控制在設定限值以內,從而完全消除Δn超限現象。

3.3 抑制參數超限的綜合算法

基于前面設計的不同算法在抑制Δn參數超限中的性能,綜合各算法有效性設計了解決Δn超限問題的新算法。算法基本原理如下:

(1)采用原星歷擬合算法解算星歷參數時如果發現參數超限則啟動新算法;

(2)算法中采用了固定Δn參數、參數嶺估計、調整擬合弧長的策略。

基于12月份系統中3顆GEO衛星的定軌實測數據對新算法進行了星歷擬合驗證,擬合結果表明,在新算法條件下,3顆 GEO衛星擬合結果超限現象完全消除。3顆衛星12月份擬合結果如圖15～圖17所示。

圖15 2010-12月 GEO-A新算法擬合Δn曲線Fig.15 Δn fitting result with new algorithms of GEO-A

圖16 2010-12月 GEO-B新算法擬合Δn曲線Fig.16 Δn fitting result with new algorithms of GEO-B

圖17 2010-12月 GEO-C新算法擬合Δn曲線Fig.17 Δn fitting result with new algorithms of GEO-C

4 結束語

提高星歷擬合精度是保證衛星導航系統精度的重要因素之一,針對實際工程中出現的 GEO衛星星歷參數超過接口范圍并導致用戶定位出現誤差的現象,從數學機理和衛星動力學規律等多方面分析 GEO衛星星歷參數超限的原因,指出月球攝動力和解算方程病態性的綜合因素導致GEO的衛星星歷擬合參數超限;基于 GEO衛星實際測定軌數據的特性,設計固定部分參數、調整擬合弧段以及進行有偏估計等抑制參數超限的算法,并通過實際測定軌數據進行驗證。試驗結果表明:三種方法對于抑制星歷超限都有明顯效果,基于三種方法原理設計的新算法能夠有效解決參數超限問題。

[1] HU Songjie.Research on the Broadcast Ephemeris Parameters of GPS and GLONASS[J].Journal of Spacecraft TT and C Technology,2005,26(3):5-8.(胡松杰.GPS和GLONASS廣播星歷參數分析及算法[J].飛行器測控學報,2005,26(3):5-8.)

[2] CUI Xianqiang,JIAO Wenhai,JIA Xiaolin,et al.Comparisons of two Kinds of GPS Broadcast Ephemeris Parameter Algorithms[J].Chinese Journal of Space Science,2006,26(5):382-387.(崔先強,焦文海,賈小林,等.兩種 GPS廣播星歷參數算法比較[J].空間科學學報,2006,26(5):382-387.)

[3] CUI Xianqiang.Solving Similar GPS Broadcast Ephemeris Parameters Using Givens Transfomation[J].Engineering of Surveying and Mapping,2006,28(4):22-25.(崔先強.用基于Givens變換的QR分解計算類 GPS廣播星歷參數[J].測繪工程,2006,28(4):22-25.)

[4] CHEN Liucheng,HAN Chunhao,CHEN Jingping.The Research ofSatellites BroadcastEphemerisParameters Fitting Arithmetic[J].Science of Surveying and Mapping,2007,32(3):12-14.(陳劉成,韓春好,陳金平.廣播星歷參數擬合算法研究[J].測繪科學,2007,32(3):12-14.)

[5] HUAN G Yong,HU Xiaogong,WAN G Xiaoya,et al.Precision Analysis of Broadcast Ephemeris for Medium and High Orbit Satellite[J].Process in Astronomy,2006,24(1):81-87.(黃勇,胡小工,王小亞,等.中高軌衛星廣播星歷精度分析[J].天文學進展,2006,24(1):81-87.)

[6] CUI Xianqiang,J IAO Wenhai,J IA Xiaolin,et al.The Fitting Algorithm of GPS Broadcast Ephemeris Parameters[J].Journal of Institute of Mapping and Surveying,2004,21(4):244-246.(崔先強,焦文海,賈小林,等.GPS廣播星歷參數擬合算法[J].測繪學院學報,2004,21(4):244-246.)

[7] GAO Yudong,XI Xiaoning,WANG Wei.An Improved Fitting Algorithm Design of Broadcast Ephemeris for GEO Satellite[J].Journal of National University of Defense Technology,2007,29(5):18-22.(高玉東,郗曉寧,王威.GEO導航星廣播星歷擬合改進算法設計[J].國防科學技術大學學報,2007,29(5):18-22.)

[8] YANG Weilian.Spectral Analysis of Satellite Orbit Per turbation[J].Journal of Astronautics,1995,16(4):1-8.(楊維廉.衛星軌道攝動頻譜分析[J].宇航學報,1995,16(4):1-8.)[9] YAN G Weilian.An Accurate Mathematical Model for Satellite Ephemeris[J].Chinese Journal of Space Science,1999,19(2):148-153.(楊維廉.一種高精度的衛星星歷模型 [J].空間科學學報,1999,19(2):148-153.)

[10] DING Wenwu,LIU Wanke,LI Zhenghang.Satellites Broadcast Ephemeris Based GPS Coordinate Polynomial Fitting Algorithm[J]. Hydrographic Surveying and Charting,2007,27(6):4-7.(丁文武,劉萬科,李征航.基于廣播星歷的GPS衛星坐標的多項式擬合算法[J].海洋測繪,2007,27(6):4-7.)

[11] CHEN Zhengyang,YI Chonghai.Using Chebyshev Polynomials to GPS Satellite Orbit Standardized[J].Mine Surveying,2002(2):5-7.(陳正陽,易重海.用切比雪夫多項式進行 GPS衛星軌道標準化[J].礦山測量,2002(2):5-7.)

[12] YOUSIF H,RABBAN Y A E.Assessment of Several Interpolation Methods for Precise GPS Orbit[J].THE Journal of Navigation,2007,60(3):443-455.

[13] J EFFERSON D,BAR S Y.Accuracy and Consistency of Broadcast GPS Ephemeris Data[C]∥Proceedings of IONGPS-2000.Salt Lake City:[s.n.],2000:391-395.

(責任編輯:宋啟凡)

Ephemeris Fitting and Experiments Analysis of GEO Satellite

HE Feng1,2,W ANG Gang1,LIU Li1,CHEN Liucheng1,HU Xiaogong2,HUANG Y ong2,SONG Yezhi2,RUAN Rengui3
1.Beijing Global Information Application and Development Center,Beijing 100094,China;2.Shanghai Astronomical Observatory,Chinese Academy of Sciences,Shanghai 200030,China;3.Xi’an Institute of Surveying and Mapping,Xi’an 710054,China

The phenomenon and regulation of parameter’s exceeding limitation in the operation of system are introduced,and then the reasons are illustrated according to the ill-conditioned equation and the orbital characteristics,some fitting algorithms are designed on the condition of avoiding accuracy losing,and the experiments are carried out with the actual observation data.The results show that it is efficient to eliminate the parameter exceeding for the method of fixing one parameter while computing the others or the method of parameter ridge estimate.

GEO;ephemeris fitting;correlation;ridge estimate

HE Feng(1982—),male,engineer,majors in satellite navigation and precise surveying and controlling technology.

P135

:A

1001-1595(2011)S-0052-07

2011-01-31

修回日期:2011-03-15

何峰(1982—),男,工程師,研究方向為衛星導航與精密測量控制技術。

E-mail:chcocu82815@yahoo.com.cn