汽輪發電機組軸系扭振響應分析

向 玲, 陳秀娟, 唐貴基

(華北電力大學 能源動力與機械工程學院,機械工程系,保定071003)

隨著現代電力工業的發展,我國已進入大機組與大電網的發展階段.近年來發現,電力系統發生擾動時,如負載突然變化、故障以及調整控制設備等,發電機繞組內部將產生較大的瞬變電磁轉矩,使軸系失去平衡,從而激起汽輪發電機組軸系扭振,這一過程雖然短暫,卻可能導致主軸或連接螺釘斷裂、飛脫,甚至人身傷亡等嚴重后果,造成巨大的經濟損失.據資料顯示,近年來國內外因扭振引起的機組損傷事故高達30多起[1].扭振問題受到國內外的廣泛關注.然而目前在實際機組上進行軸系扭振研究還存在一定的局限性,特別是研究電力系統擾動下的扭振響應更具有一定的危險性.因此,對電力系統擾動下的扭振進行仿真研究具有重要的實際意義.

軸系扭振響應的計算方法主要有模態疊加法、直接積分法和傳遞矩陣法等[2].傳統的汽輪發電機組軸系扭振瞬態響應求解模型是基于多段集中質量模型,將Riccati傳遞矩陣法和Newmark-β法相結合建立的,由于Newmark-β法中進行了線性假設,其計算結果存在較大的線性累積誤差.筆者對其進行了去線性趨勢處理,消除了累積誤差,對原有模型進行了修正.利用該方法,以300 MW汽輪發電機組扭振模擬機為例,對其在典型電力系統擾動(如三相短路、兩相短路、非同期并網等)下的軸系扭振瞬態響應進行了仿真和分析.

1 汽輪發電機組軸系數學模型

建立可靠準確的軸系模型是進行仿真的前提,多段集中質量模型是多質量塊的質量-彈簧系統,可較準確地反映低階和高階的扭振特性,盡管計算精度受質量分塊數的影響,但可以滿足工程計算要求,目前被廣泛采用[3-4].圖1為多段集中質量模型示意圖.

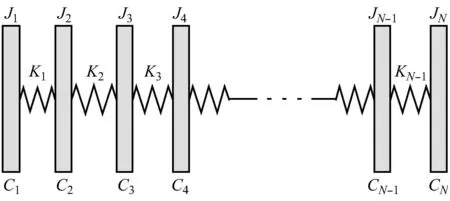
圖1 多段集中質量模型Fig.1 Schematic diagram of the multi-mass model

若加入各個質量塊所受外加力矩Tti,則多段集中質量模型的振動微分方程可簡化成矩陣形式:

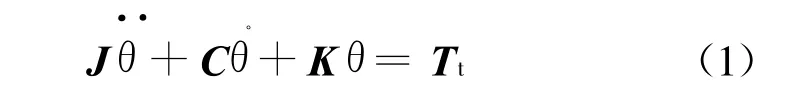
式中:J表示系統的轉動慣量矩陣;C表示系統的阻尼矩陣;K表示系統的剛度矩陣;T t表示系統所受的外加力矩向量分別表示系統各個點的扭轉角加速度、角速度和角位移.

2 機組軸系扭振瞬態響應求解模型

2.1 Newmark-β法的增量表達式

逐步積分法是目前求解非線性方程的一種有效方法.它在一個時間步長內,將非線性系統近似為線性系統,系統特性由該區間起點狀態確定.Newmark-β法和傳遞矩陣法相結合求解軸系扭振響應的思路為:首先將Newmark-β法的表達式改造成增量表達式;然后利用該增量表達式,推導軸系典型部件的增量傳遞矩陣表達式;最后對增量傳遞矩陣表達式進行Riccati變換,得到遞推公式.

根據Newmark-β法[5],t+Δt時刻的角速度和角加速度表達式為:

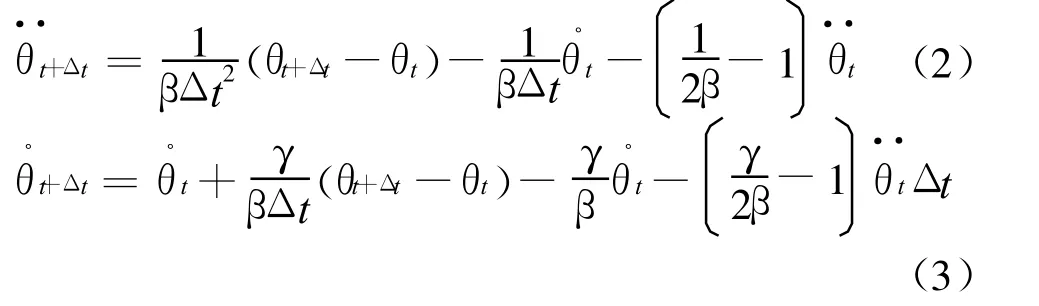
式中:γ、β是Newmark-β法的參數.將上兩式改造成增量表達式:

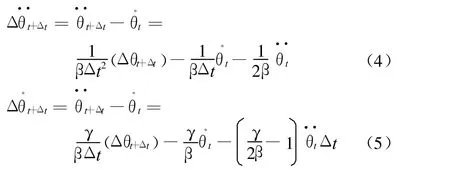
式(4)和式(5)可用于求解非線性方程,它描述了Δt時段內速度和加速度增量的變化關系.

2.2 典型單元的扭振傳遞方程

從圖1多段集中質量模型中取出一個典型單元(一個剛性圓盤和一個彈性軸段)進行分析.

(1)對于剛性圓盤,其所受扭矩有慣性力矩、阻力矩、左右截面扭矩差及外力矩,根據力矩平衡條件,寫成增量表達式為:

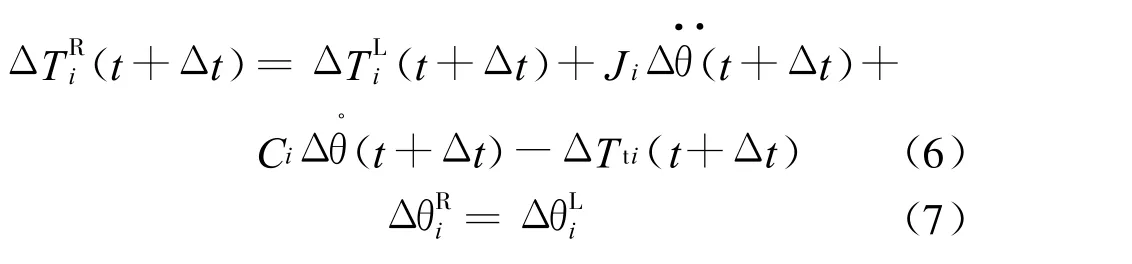
將式(4)、式(5)代入式(6),整理得

(2)對于無質量的彈性軸段,可得下列增量關系式:

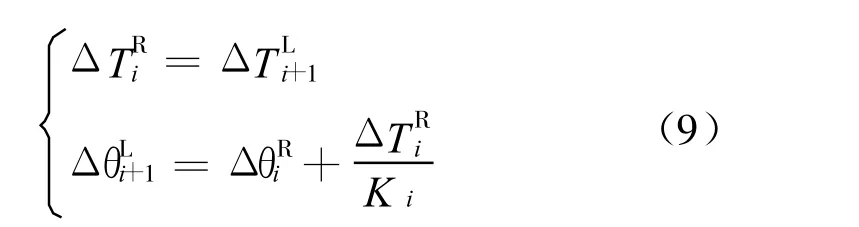
(3)對于單元軸段,設fi=ΔTi,ei=Δθi,則單元軸段傳遞矩陣為:

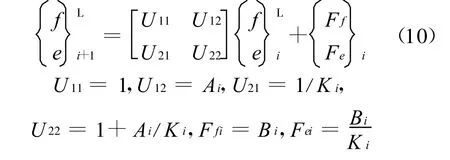
設Riccati變換為:

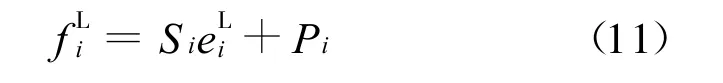
將式(11)代入式(10)得:

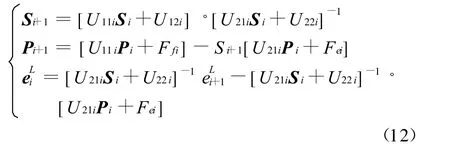
由上式可得傳遞矩陣Si、Pi及eLi的遞推公式.

2.3 瞬態響應求解過程

在分析軸系扭振時,系統兩端自由,故其邊界條件如下.

對于左端面:

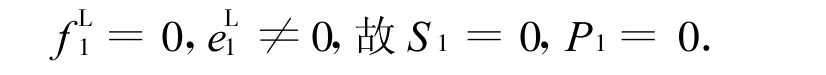
對于右端面:

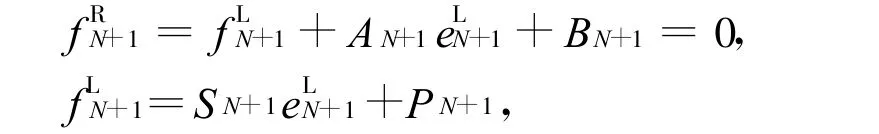
利用邊界條件及傳遞矩陣遞推公式可由右到左計算出各個結點在t+Δt瞬時的角位移增量eLi(i=N,N-1,…,1)及各個截面的扭矩增量fLi.根據前述兩種方法反復迭代計算,可得到系統各個瞬時各個結點的扭轉角位移、角速度、角加速度響應和各個截面的扭矩增量響應,計算步驟如下:

(1)將軸系模化成N段集中質量模型,確定各個物理參數Ji、Ci、Ki及外加力矩增量 ΔTti.

(3)計算 傳遞矩陣參數Ai、Bi、U11、U12、U21、U22、Ffi、Fei.

(4)根據傳遞矩陣遞推公式計算Si、Pi.

(5)根據遞推公式和邊界條件計算各結點在t+Δt 時刻的狀態矢量增量(eLi、fLi).

(6)利用Newmark-β增量法,根據式(4)和式(5)得到t+Δt時刻扭轉角加速度和角速度的增量從而得到該時刻的角加速度(t+Δt)和角速度(t+Δt).

(7)根據t+Δt時刻)和eLi可得t+2Δt時刻的扭轉角位移θ(t+2Δt).

2.4 誤差消除處理

在上述計算過程中,認為 Δt時段內系統為線性,故計算結果存在線性累積誤差,為消除此線性趨勢項,需對計算進行改進.在計算步驟(6)時,由系統增量運動方程求出,而不由公式(4)求出;最后對步驟(7)中算出的各個時刻各個結點角位移)用最小二乘法進行去線性趨勢項處理.

圖2為低壓缸轉子消除累積誤差前后時域曲線對比圖.由圖2可知,未經上述處理步驟的時域曲線存在較大的線性累積誤差和較嚴重的線性趨勢,而經過誤差處理的曲線則更為合理.結合圖5(a)頻域曲線可知,處理后的時域曲線能夠得到扭振的前五階固有頻率,本文的處理方法是有效和可行的.

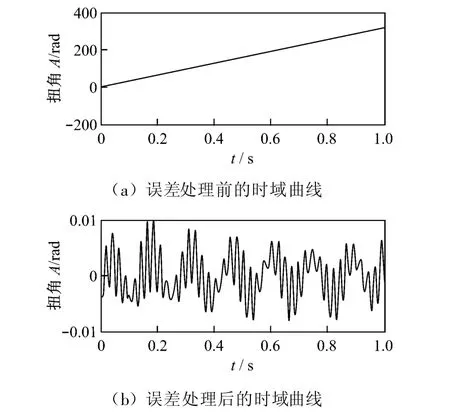
圖2 低壓缸轉子誤差處理前后時域曲線對比Fig.2 Time-domain curves of low-pressure cylinder before and after elimination of cumulative errors

3 實例分析

能引起機組較嚴重扭振的典型電氣擾動有發電機出口端短路和非同期并網等[6].筆者應用Matlab編寫軸系扭振響應仿真程序,以300 MW汽輪發電機組為例,分析了其軸系在典型電氣擾動下的扭振瞬態響應.

模擬機的主要設計參數與被模擬對象東方300 MW汽輪發電機組基本吻合[7-8],其額定功率為15 k W,工作轉速為3 000 r/min,頻率為50 Hz.軸系的計算值與測試值基本吻合,見表1.

3.1 發電機出口端短路故障

在電力系統中發電廠附近,特別是在發電機出口發生短路故障時,將出現很大的短路電流和沖擊力矩.在各種短路故障中,發電機出口三相短路和兩相短路對軸系的影響較嚴重.

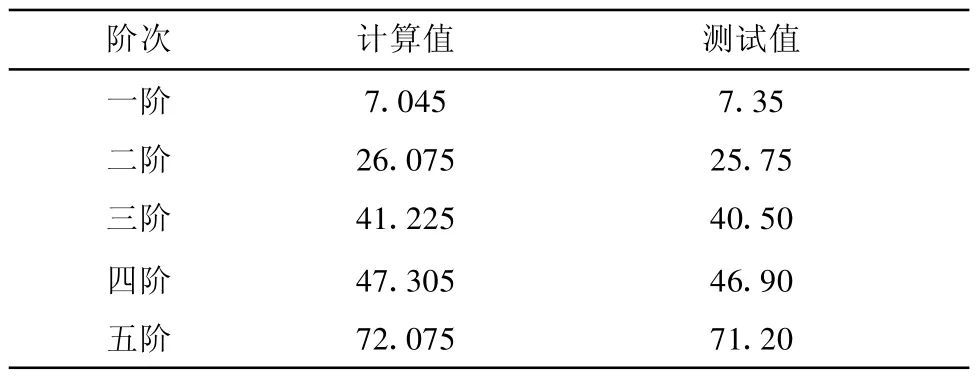
表1 軸系扭振前五階固有頻率Tab.1 System natural frequencies Hz

3.1.1 短路電磁力矩特性

三相短路和兩相短路電磁力矩特性曲線(圖3)可用西屋公司提供的下述方程描述.

(1)三相短路電磁力矩

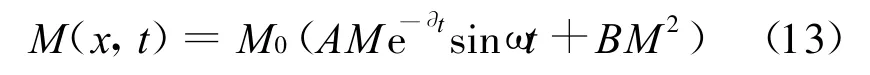
式中:A=6.259;B=0.087 7;?=3.980 9;ω=2πn/60;n為發電機的工作轉速;M0為正常運行狀態下發電機的額定轉矩.

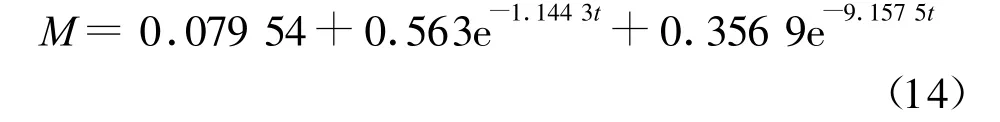
(2)兩相短路電磁力矩

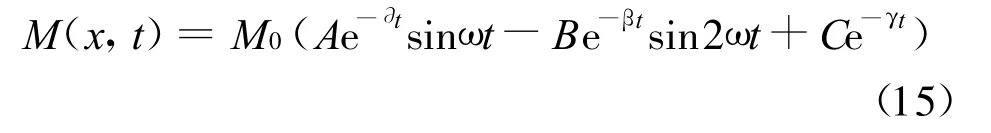
式中:A=7.591;B=3.795;C=0.742;?=5.305;β=2.65;γ=4.428;ω=2πn/60.

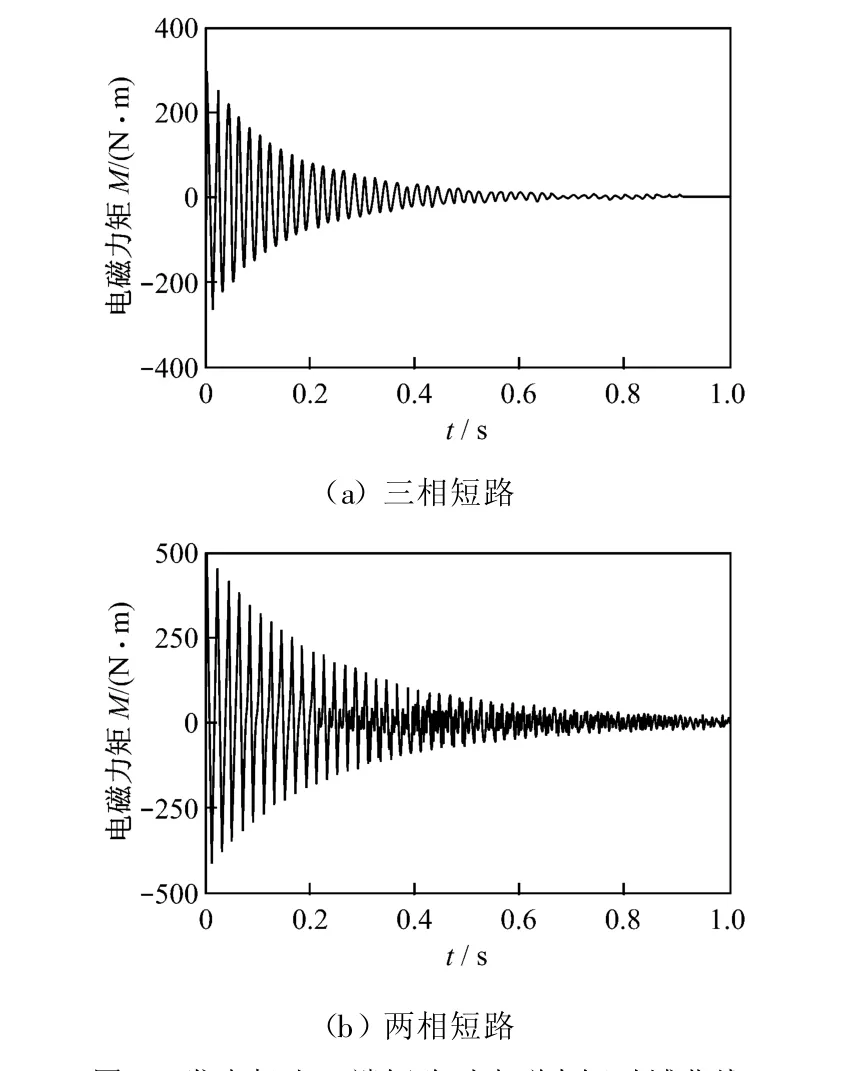
圖3 發電機出口端短路時電磁力矩時域曲線Fig.3 Electromagnetic torque curves for a short circuit fault at generator outlet

3.1.2 短路時的扭振時頻響應曲線

圖4和圖5分別為機組軸系在三相短路和兩相短路時,典型結點低壓缸和發電機轉子的扭振時頻響應曲線圖.

在圖4中,除含有工頻50 Hz成分外,軸系的前五階固有頻率均被不同程度激起,低壓缸轉子主要以第三階和第一階頻率成分為主導,其次為第四階頻率成分,第二階頻率成分最小.而對發電機轉子來說,軸系的前四階頻率成分均為主要組成部分,工頻幅值也有所增加.圖5中兩相短路時的扭振時域特征與三相短路時相似,但在頻譜圖中出現100 Hz倍頻成分.與圖4頻譜圖相比,除第一階和第二階頻率成分無明顯變化外,其他成分均有所下降,兩相短路激起的扭轉振動強度更大.

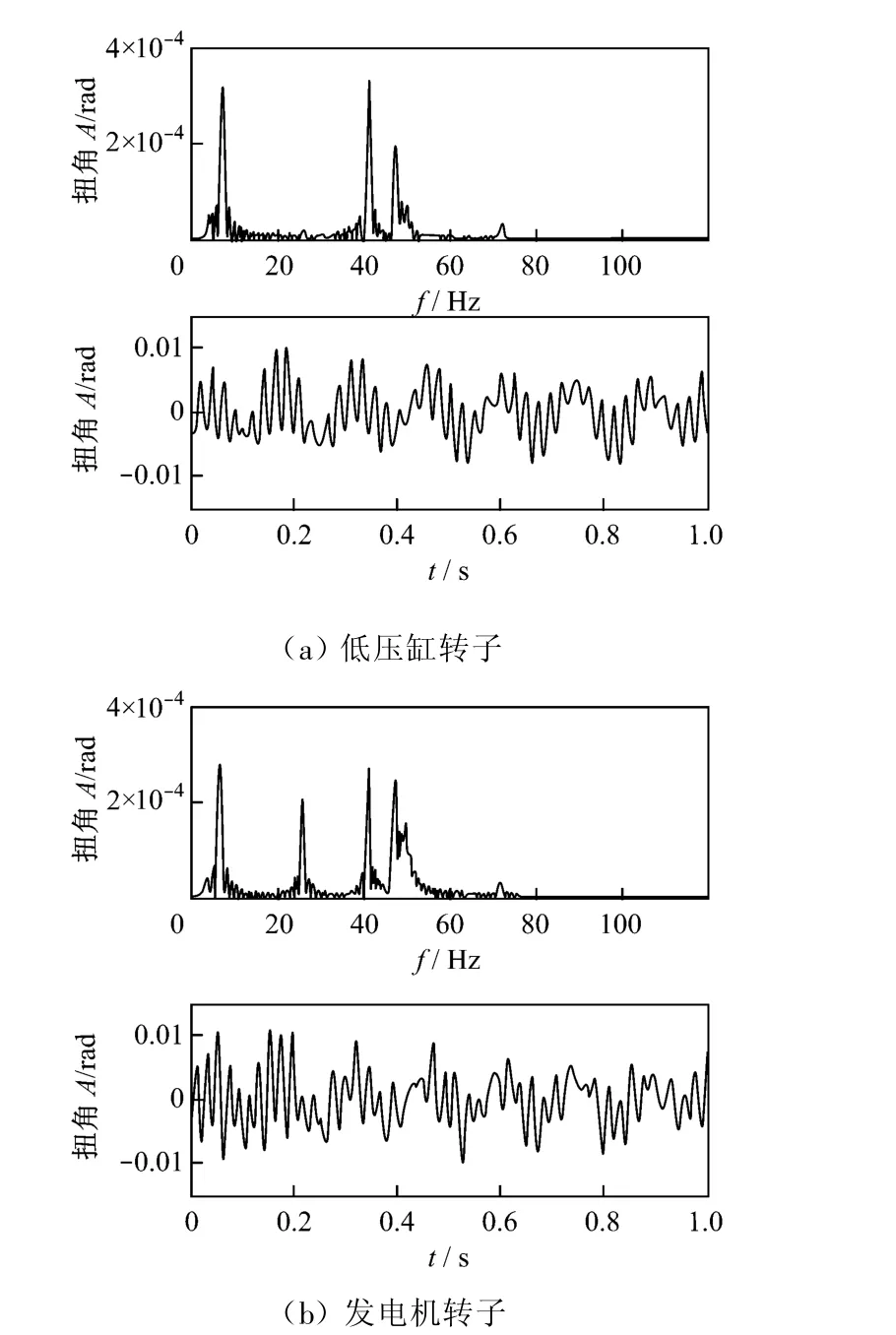
圖4 三相短路故障下軸系扭振時頻響應曲線Fig.4 Time and frequency responses of shaft torsion vibration caused by three-phase short circuit fault

3.2 非同期并網故障

3.2.1 非同期并網電磁力矩特性

非同期并網將產生較大的沖擊電流和電磁轉矩,是機組在運行過程中可能遭受的典型電氣干擾之一.從電磁力矩的角度看,合閘角在120°左右時,電磁力矩最大,產生的軸系扭振最嚴重.發電機120°和180°非同期并網時,暫態過程電磁轉矩特性曲線見圖6.

圖6中的曲線可用下列方程描述.

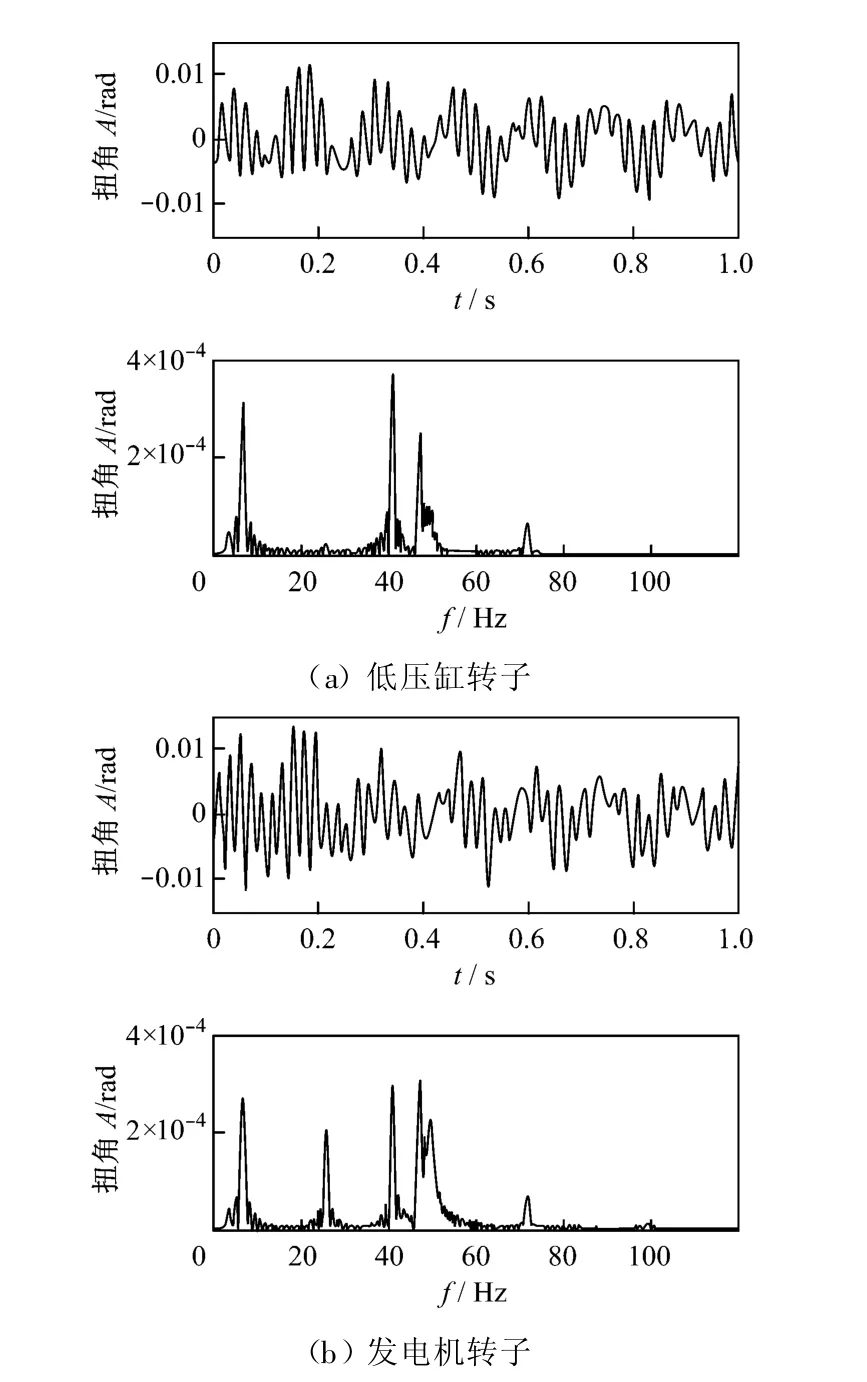
圖5 兩相短路故障下軸系扭振時頻響應曲線Fig.5 Time and frequency responses of shaft torsion vibration caused by two-phase short circuit fault

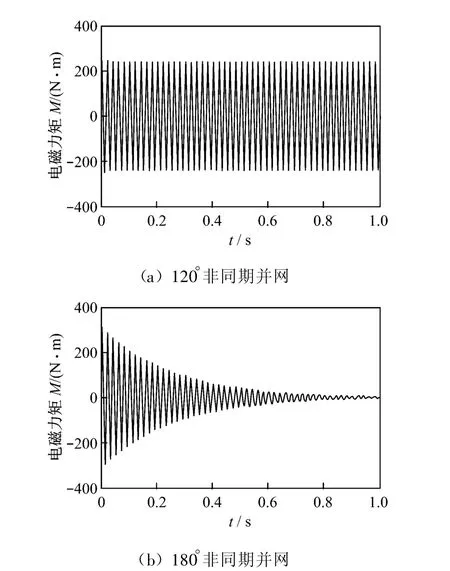
圖6 發電機非同期并網時電磁力矩時域曲線Fig.6 Electromagnetic torque curves at the time of asynchronous juxtaposition

(1)120°非同期并網電磁力矩

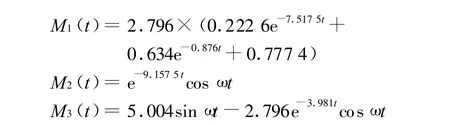
(2)180°非同期并網電磁力矩

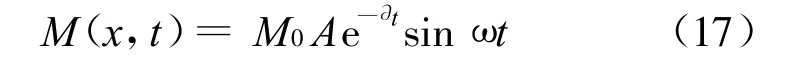
式中:A=6.617 2;?=3.980 9;M0同前.

3.2.2 非同期并網軸系扭振時頻響應曲線

圖7和圖8分別為機組軸系在非同期并網時低壓缸轉子和發電機轉子的扭振響應及頻譜分析圖.低壓缸轉子在120°非同期并網時激起的第一階固有頻率明顯高于180°非同期并網時的數值,其他頻率成分均變化不大.對于發電機轉子,在120°非同期并網時工頻50 Hz成分和第二階固有頻率比低壓缸轉子的同階頻率明顯增大,其他成分基本不變;與180°非同期并網相比,其工頻和第一階固有頻率也有明顯增大.以上分析與兩相短路時的情況也大致相同,可見,120°非同期并網激起的軸系扭振響應最大.

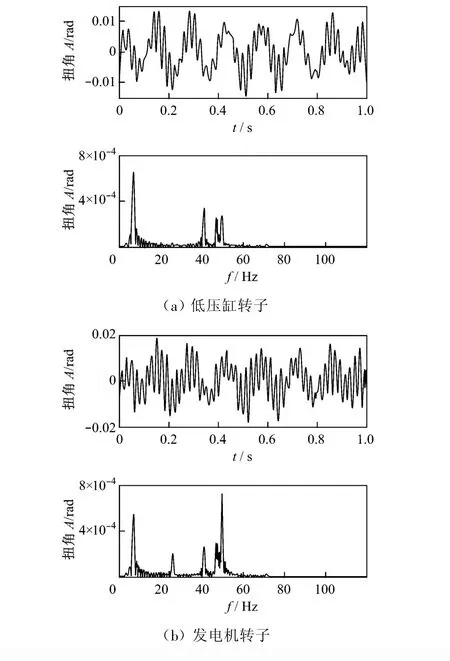
圖7 120°非同期并網時軸系扭振時頻響應曲線Fig.7 Time and frequency responses of shaft torsional vibration caused by 120°asynchronous juxtaposition

3.3 各種故障下軸系扭角有效值的對比

圖9為機組軸系在各種故障下的軸系扭角有效值對比,其中120°非同期并網時軸系扭角響應最大,其次是兩相短路和180°非同期并網,三相短路時軸系扭角響應最小,各種故障下發電機轉子比低壓缸轉子振動幅值大.

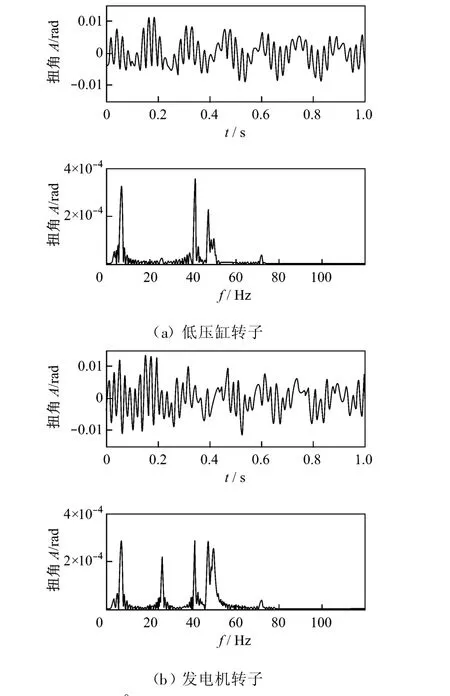
圖8 180°非同期并網時軸系扭振響應曲線Fig.8 Time and frequency resp onses of shaft torsional vibration caused by 180°asynchronous juxtaposition

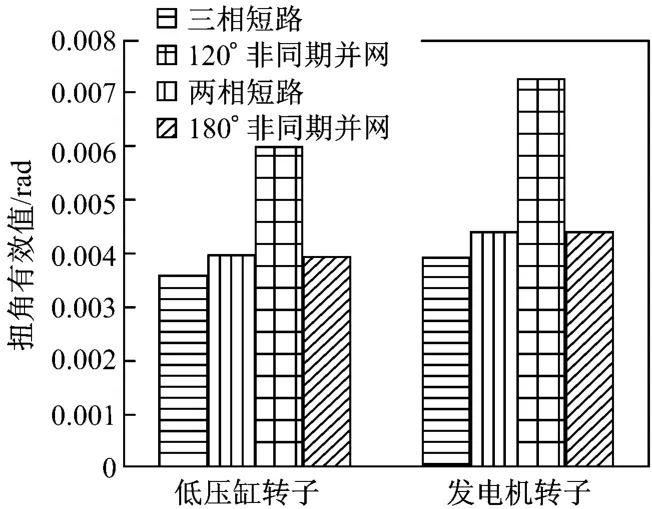
圖9 各種擾動下扭角有效值的比較Fig.9 Comparison of effective torsional angle valuesat different disturbances

4 結 論

(1)幾種典型電力系統擾動均能不同程度地激起軸系的前五階扭轉固有頻率.

(2)120°非同期并網激起的軸系扭振響應最大,其次為兩相短路和180°非同期并網,三相短路時軸系扭振響應最小.

(3)在整個軸系的扭振響應上,發電機轉子處扭振比低壓缸轉子處更劇烈.

[1] 張俊紅,高文志,付魯華.大型汽輪發電機組軸系振動及其控制的研究[J].動力工程,2003,23(4):2490-2494. ZHANG Junhong,GAO Wenzhi,FU Luhua.Research on the shaf ting vibration and its control in big turbogenerator unit[J].Journal of Power Engineering,2003,23(4):2490-2494.

[2] RATAN S,RODRIGUEZ J.Transient dynamic analysis of rotor using SMAC techniques[J].Journal of Vibration and Acoustics ASME,1992,1l4(3):447-448.

[3] FAIRBAIM R E.Turbinegenerator torsional mechanical modal parameter identification from on-line measurements[J].IEEE Trans on Power Systems,1991,6(4):1389-1395.

[4] ZHANG Junhong,HAO Zhiyong,FU Luhua.Modeling and calculation of the natural frequency of 300 MW turbo-generator rotor shaft system[J].Transactions of Tianjin University,2001,7(2):93-97.

[5] 張雄,王天舒.計算動力學[M].北京:清華大學出版社,2007.

[6] 張保會,余穎輝.電氣操作對機組軸系扭振的影響機理[J].中國電機工程學報,2001,21(8):24-28. ZHANG Baohui,YU Yinghui.Analysia for the effect of electrical operation on turbine-generator's shaft torsional oscillation[J].CSEE,2001,21(8):24-28.

[7] 向玲,唐貴基,朱永利.300 MW汽輪發電機組在機電耦合作用下的扭振[J].動力工程,2007,8,27(6):492-495. XIANG Ling,TANG Guiji,ZHU Yongli.Research for the torsion vibration in mechanical-electrical coupling on 300 MW turbo-generator rotor system[J].Journal of Power Engineering,2007,27(6):492-495.

[8] 向玲,唐貴基,朱永利.汽輪發電機組次同步諧振及軸系扭振試驗研究[J].華北電力大學學報,2005,32(4):85-87. XIANG Ling,TANG Guiji,ZHU Yongli.Experimental research of subsynchronous resonance and torsion vibration on turbo-generator rotor shaft units[J].Journal of North China Electric Power University,2005,32(4):85-87.