基于小波變換與低通濾波的多源圖像融合方法

陳 丹

（華東交通大學 軟件學院，江西 南昌 330013）

基于小波變換與低通濾波的多源圖像融合方法

陳 丹

（華東交通大學 軟件學院，江西 南昌 330013）

在多尺度分解的框架下，對像素級的多源圖像融合，提出一種基于低通濾波與小波變換的圖像融合算法.先將低空間分辨率的多光譜圖像插值，使之具有與高空間分辨率全色圖像相同的分辨率，然后再對多光譜圖像低頻分量和全色圖像低頻分量進行融合處理，得到一幅具有高空間分辨率的多光譜圖像.將全色圖像的低頻分量和多光譜圖像的低頻分量進行融合，以達到增強光譜圖像的低頻分量空間特性效果.

低通濾波；小波變換；圖像融合

1 引言

圖像融合是根據一種有效的算法，將從不同傳感器得到的圖像進行綜合處理，得到一幅新的滿足某種要求的圖像.融合后的圖像應該比原圖像更加清晰可靠，易于分辨，融合的圖像可用于圖像銳化，圖像分割、目標識別等.隨著人們對圖像融合技術的研究，現在融合技術以在諸多方面得到廣泛的應用[1,2].多源圖像的融合有IHS變換融合算法、PCA變換融合算法、高通濾波(HPF)融合算法與小波變換融合算法等[3,4].與傳統的數據融合方法相比，小波變換融合具有多分辨率的特性，是一類很重要的融合算法，它雖然能使融合圖像在獲得高空間分辨率的同時，較好地保持了原始光譜信息，使得它在遙感數據融合領域具有較大的優勢，但由于它舍棄了高分辨率圖像的低頻分量，故很容易出現分塊效應[5].本文提出了一種基于低通濾波與小波變換相結合的多源圖像融合算法，并給出了圖像融合結果的定性評價和定量評價，結果表明該算法能得到較好的融合效果.

2 基于小波變換理論與低通濾波相結合的圖像融合算法

在傳統的小波變換增強方法中，是直接利用經小波分解的具有高空間分辨率的全色圖像的細節分量替換多光譜圖像的細節分量，然后進行小波反變換從而得到增強后的多光譜圖像[6].由于其直接舍棄了全色圖像的低頻分量，因此在增強結果中容易出現分塊效應針對傳統小波變換增強方法的這些缺點[7,8]，為盡可能地保持多光譜圖像的光譜特性，先對多光譜圖像和高空間分辨率的全色圖像只進行一階小波分解，然后通過將全色圖像的低頻分量和多光譜圖像的低頻分量進行融合，以達到增強光譜圖像低頻分量空間特性的目的，克服因小波分解階數低而造成的增強效果不明顯的缺點；同時，通過融合也提高了多光譜圖像低頻分量與全色圖像低頻分量的相關性，避免了增強結果出現分塊效應.

設高分辨率圖像H(i,j)和多光譜圖像L(i,j)經小波分解后的低頻分量分別為HL（i，j）和LL（i，j），將HL（i，j）進行低通分解，獲得低頻分量HLL（i，j），分解算子為：

ω=HL（i，j）-HLL（i，j）為全色圖像低頻分量HL（i，j）的細節成分.然后以LL（i，j）+ω重構多光譜圖像低頻分量LL（i，j），這樣便使多光譜圖像低頻分量LL（i，j）融合了全色圖像低頻分量HL（i，j）的細節成份，從而增強了多光譜圖像低頻分量LL（i，j）的空間特性，同時也提高了多光譜圖像低頻分量與全色圖像低頻分量的相關特性.

具體的融合算法步驟如下：

（1）對TM多光譜圖像進行低空間分辨率的多光譜圖像雙線性插值,使之具有與高空間分辨率全色圖像相同的分辨率.

（2）分別對SPOT圖像、插值后的TM圖像進行小波變換，得到各自相應分辨率的低頻圖像和高頻細節圖像；本文中選用Daubechies的D4作為小波基，小波變換級數n=2；

（3）將小波分解后的多光譜圖像低頻分量和全色圖像低頻分量進行融合處理,即首先對全色圖像的低頻分量進行低通分解,得到其低頻分量的低頻成份和細節成份,然后用多光譜圖像的低頻分量與全色圖像低頻分量的細節成份重構多光譜的低頻分量；

（4）用全色圖像高頻細節分量直接替換多光譜圖像的高頻細節分量,并對替換后的多光譜圖像進行小波逆變換,從而得到增強的多光譜圖像；

由于遙感圖像的數據量巨大，在對低分辨率多光譜圖像插值時，大多采用近鄰法.但這種對像素置換方法的簡單性,會對最終的融合效果產生一定的影響.為此，需要引入新的插值方法.按照經典的數學理論,本文引用了雙線性插值模型如圖1所示.

圖1 雙線性插值模型

模型的計算式為：設像素點(x,y)及其四周圍的點(0,0)、(0,1)、(1,0)、(1,1)對應的圖像灰度值分別為 f(x,y)、f(0,0)、f(0,1)、f(1,0)和 f(1,1),則通過 x 軸的一階線性插值,得：

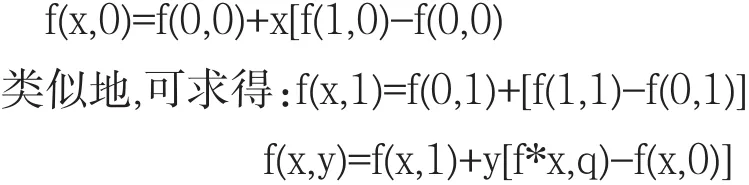
對多光譜圖像進行雙線性插值后,它與全色圖像的空間分辨率相等.

3 實驗結果及分析

采用各小波融合模式，通過Matlab7.0程序實驗得到圖像融合結果如圖2所示：

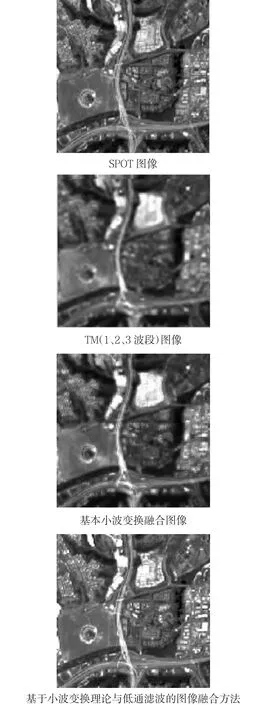
圖2 兩種方法融合圖像結果

從視覺效果上來看，新方法的結果圖像保留了多光譜圖像的絕大部分光譜信息，在細節信息上具有明顯的改善.與作者前期研究成果文獻【9】中的IHS變換融合方法以及PCA融合方法相比較，新方法的融合圖像在光譜信息的保持上比這兩種方法的融合圖像有明顯的改善，在空間細節信息的表現能力上也有一定程度的提高.與小波變換融合方法的融合圖像相比較，新方法的融合圖像在空間細節信息的表現能力上與之相當，但光譜信息有明顯的改善，總體效果優于小波變換融合方法.

從表1中可看出，融合圖像各分量的熵要比未經融合處理的低分辨率圖像的熵大.這表明，采用小波變換進行圖像融合，均使兩類圖像的信息得到融合.并且，改進模型所獲得的圖像均比基本模型融合得到的圖像熵值大，這說明改進模型所獲得圖像的信息量增加.

4 小結

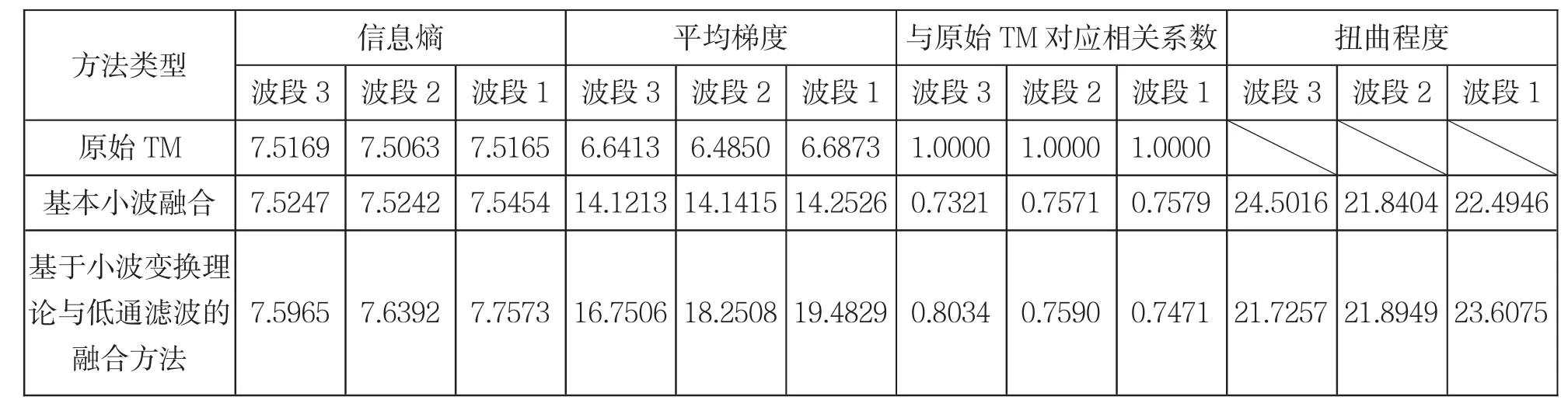
表1 幾種小波變換方法融合結果圖像統計參數對比

從上述方法的融合結果可以看出，無論是空間分辨率還是圖像的清晰程度，融合結果圖像的各項指標都比原高分辨率圖像和原低分辨率圖像以及其它融合方法好.融合后的圖像在信息量、清晰度和可判讀性上都有比較明顯的增強，這說明本文所采用的融合方法很好地保持了待融合圖像的空間信息和光譜信息.

〔1〕Chavez Pat S，Stuart C S，Jeffrey A.A Comparison of the There Different Methods to Merge Multi resolution and multi spectral Data：Land sat W and SPOT Panchromatic.Photo grammetrlc Engineering＆Romote Sensing[J].Vol.57,No.3 1991:295-303.

〔2〕T.s.huang.PCM picture transmission.IEEE Spectrum[J].Vol.2,No.12,1995:57-63.

〔3〕崔錦泰.小波分析導論[M].西安交通大學出版社,2005.

〔4〕Yocky David A.Image Merging and Data Fusion by Means of the Discrete Two-Dimensional Wavelet Transform[J].Journal of the optical Society of America,A:optics&Image Science,1995,12(9).

〔5〕Ouarab N.，A Chir M., Khettal,N.,smara,Y.Spatial enhancement of Satellite images using data fusion algorithms in the wavelet domain,Remote Sensing and Data Fusion over Urban Areas，IEEE/ISPRS Joint Workshop 2006.

〔6〕Fanelli,A.,Leo,A.,ferri,M.Remote sensing imagesdatafusion:awavelettransform approach for urban analysis Remote Sensing and Data Fusion over Urban Areas[J].IEEE/ISPRS workshop 2005.

〔7〕Pinz A.,Bartl R.information,fusion in image understanding[J].IEEE Trans Med image,1992,Vol.12(4).

〔8〕霍洪濤.小波變換在遙感影像融合中的應用研究[J].中國圖象圖形學報，2003(5).

〔9〕陳丹.基于PCA變換與小波變換的多源圖像融合方法[J].重慶科技學院學報，2010,12(2).

TP391

A

1673-260X（2011）03-0044-03