分擔集合的亞純函數的正規性

劉克笑(湖南懷化學院預科部，湖南懷化418008)

分擔集合的亞純函數的正規性

劉克笑
(湖南懷化學院預科部，湖南懷化418008)

從分擔值以及分擔集合角度出發，研究亞純函數與其高階導數分擔集合的正規性及亞純函數與其一階導數在分擔集合情況下的正規定則，結果改正推廣了前人的結果.

亞純函數;分擔值;高階導數;正規族

定義1設f與g為D內的亞純函數，a1，a2，a3為三個互相判別的有窮復數，我們稱f與g分擔集合S={a1，a2，a3}，如果

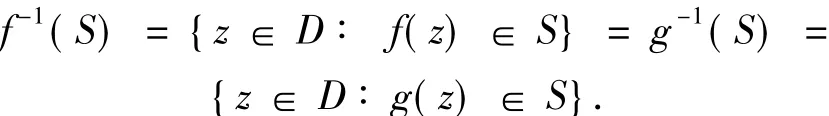
利用分擔值理論研究亞純函數的正規性是亞純函數正規族理論研究的一個重要課題，這方面工作最早由W.Schwick開始研究［1］，后來國內許多數學工作者對這方面做了許多卓有成效的工作，得到了許多重要的結果［2－5］.

在2007年，劉曉俊和龐學誠證明了［6］

定理1設F為定義在D內的一族亞純函數，a，b，c為三個互相相判別的有窮復數，如果對于任意的f∈F，f∈S={a，b，c}f/∈S，那么F在D內正規.

在2008年，劉克笑和龐學誠證明了［7］

定理2設F為定義在D上的一族亞純函數，a，b，c為三個互不相等的有窮復數，如果對于任意f∈F，f(z)=af(k)(z)=a，f∈{b，c}f(k)(z)∈{b，c}，且f－a的零點重級至少是k，那么F在D內正規.

在2010年，劉克笑證明了［8］

定理3設F為定義在D上的一族亞純函數，a，b，c為三個互不相等的有窮復數，如對于任意的f∈F，f(z)=aL(z)=a，f∈{b，c}L(f)∈{b，c}，且f－a的零點重級至少是k，這里L(f)=f(k)(z) +a1(z)f(k－1)(z)+…+ak(z)f(z)，a1(z)(i=1，2，…，k)在D內解析，那么F在D內正規.

本文繼續研究亞純函數分擔二元集合的正規性，對亞純函數族中的函數極點重數以及集合中的元素做一定的要求，得到了相應的結果.

1 相關引理

引理1［9］設F是單位圓盤D上的一族亞純函數，如果對任意f∈F，f的零點重級至少是k，及f(z)=0，存在一個正數A，使得|f(k)(z)|A(A1)，那么如果F在D上不正規，存在:

(ⅰ)實數r，0＜r＜1;

(ⅱ)點列{zn}，|zn|＜r;

(ⅲ)函數列fk∈F;

(ⅳ)正數列ρn→0+，使得gn(ζ)=fn(zn+ρnζ)在C上按球面距離內閉一致收斂于一個非常數的亞純函數g(ζ)，且g#(ζ)g#(0)=kA+1，g(ζ)的級至多是2.這里g#(ζ)=稱為球面導數.

引理2設f是C上的亞純函數，a是非零的有限復數，如果f只有有限多個零點，且Ef(0)= Ef(k)(a)，那么f是有理函數.

引理3設f是C上的亞純函數，a1，a2是兩個判別的有限復數，S={a1，a2}，如果f只有有限多個零點，且(0)=(s，f(k))，那么f是有理函數.

2 主要結果及證明

定理4設F為定義在D上的一族亞純函數，令S={a，b}，這里a，b是兩個互不相等的有限復數，如果對于任意f∈F，f的極點重數2，則滿足下列條件之一，那么F在D內正規.

⑵E(S，f)=E(S，f(k))，且a+b≠0;

證明不妨設D為單位圓盤.若F在D上不正規，由引理1有，正數列ρn→0+，點列{Zn}，|Zn|＜1函數列fn∈F，使得gn(ζ)=fn(zn+ρnζ)在C上按球面距離內閉一致收斂于一個非常數的亞純函數g(ζ)，且g(ζ)的極點重數至少是2，g(ζ)的級至多是2.

可以得到:

②{Gn(ζ)}在g(ζ)－a的零點不正規.

事實上，設存在ζ0使得g(ζ0)－a=0，若{Gn(ζ)}在ζn處正規，即存在{Gn(ζ)}的子列，不妨仍然記為{Gn(ζ)}.因為g(ζ)－a0，則由Hurwitz's定理，存在ζn→ζ0，使得fn(zn+ρnζn)= gn(ζn)=a.即G(ζ0)=0.由零點的孤立性，存在正數δ使得g(ζ)≠a在區域△δ={0＜|ζ－ζ0|＜δ}D上成立.因此對于任意的ζ∈△δ，對于充分大的n，有G(ζ)=∞，矛盾，所以斷言②成立.

設ζ0是g(ζ)－a的一個零點，再次運用引理1，有:

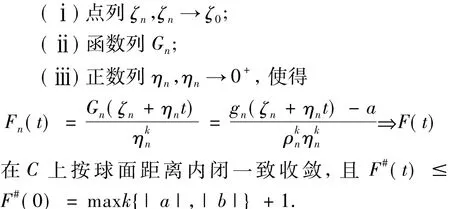
可以斷言:

③(ⅰ)F(t)僅有有限個零點;

(ⅱ)F(t)=0F(k)(t)∈S設ζ0是g(ζ)－a的k重零點，如果存在k+1個復數t1，t2，…，tk+1，使得F(tj)=0，j=1，2，…，k+1.

由于F(t)0，由Hurwitz's定理存在N，對于n＞ N，有Fn(tnj)=0，j=1，2，…，k+1.而gn(ζn+ηntn)－a=0且ζn+ηntnj→ζ0，則ζ0是g(ζ)－a的k+ 1重零點，矛盾，所以(ⅰ)成立.

可得H(t)≠0，H(t)≠∞，且H(t)是一個有理函數，于是H(t)是一個常數，這與F(t)是多項式矛盾.

設F(t)的次數q2，且qk，q＜k是不可能的.否則F(k)(t)≡0，這與珔E(S，f)=珔E(S，f(k))矛盾.當q=1時由上面的證明這是不可能的.

情形1 q3.

定理5設F為定義在D上的一族亞純函數，令S={a，b}，這里a，b是兩個互不相等的有限復數，如果對于任意f∈F，f的極點重數2，E珔(S，f)=E珔(S，f/)，f/(z)－a或f/(z)－b僅有簡單零點，且na+mb≠0，這里m，n均為整數，則F在D內正規.

證明對定理4⑴中取k=1，由定理1⑴的證明，只須證明ab≠0的情形即可.證明方法與過程和定理4相似，不再重復.

［1］Schwick W.Sharing values and normality［J］.Arch Math，1992，59:50－59.

［2］Pang X C，Zalcman L.Normality and shared values［J］.Ark Mat，2000，3:171－182.

［3］Chang JM.A normal family of concerning shared value［J］.Science in china press，2009，4:399－404.

［4］Pang X C.Shared values and normal Families［J］.Analysis，2002，5:175－182.

［5］Pang X C，Zalcman L.Normality and shared values［J］.Bull London Math Soc2000，2:325－331.

［6］Liu X J，Pang X C.Shared values and noamal families［J］.Acta Math Sin－Chinese Ser，2007(2):409－412.

［7］LIU K X，Pang X C and Liu X J.Normality concerning higher derivative in meromorphic functions and shared values［J］.Journal of kashgar teachers college，2009，3:13－15.

［8］LIU K X.A Normal Family Of Concerning Shared Value［J］.Journal of Guizhou Normal Uniwersity(Natural Sciences)，2010，3:69－72.

［9］PANG X C.Blochand normal criterion［J］.Sci China ser A，1989，32:782－791.

(責任編輯:王宏志)

Abstract:Researching the problem ofmeromorphic functions and its higher derivative shared values，and using the idea of shared－set，we prove result on normal families ofmeromorphic functions that share setwith derivatives，which improve some result given by the predecessors.

Key words:meromorphic function;shared value;higher derivative;normal family

Normality of M eromorphic Functions Concerning Shared－set

LIU Ke－xiao
(Preparatory Department，Huaihua University，Huaihua，Hunan 418008，China)

O174.52

A

1008－7974(2011)04－0003－04

懷化學院青年基金(HHUQ2009－17).

2011－01－06

劉克笑(1973－)，湖南辰溪人，碩士，湖南懷化學院預科部講師.