一類橢圓型方程弱解的正則性

狄華斐，周道軍，鄭治波

(1.云南民族大學數學與計算機科學學院，云南 昆明 650500;2.云南師范大學數學學院，云南 昆明 650092)

現代橢圓型方程問題的可解性的研究總是在合適的泛函空間中考慮其弱解的性質，所以sobolev空間的引進為這一研究提供了有效途徑［1－2］.通過 sobolev 空間，我們可以在更廣泛的函數類中尋求問題的解，這樣可解性的問題變得就容易多了.這種解往往就稱為“弱解”或“廣義解”.

本文討論橢圓型方程:

在一定的條件假設下弱解的正則性問題.近年來，這類橢圓型方程很多學者已經對它進行了廣泛的研究［2－4］.這些文獻假設算子 L的系數 aij，bi，c是光滑的.在本文中，我們對L的系數的范圍進一步放寬，在這里只要求aij∈Cm+1(U)，bi，c∈Wm，∞(U)，則得到與文獻［2］同樣的結論.

我們假設U?Rn是一個有界開集.u∈H10(U)是橢圓型方程Lu=f in U的一個弱解，在這里L擁有散度形式:

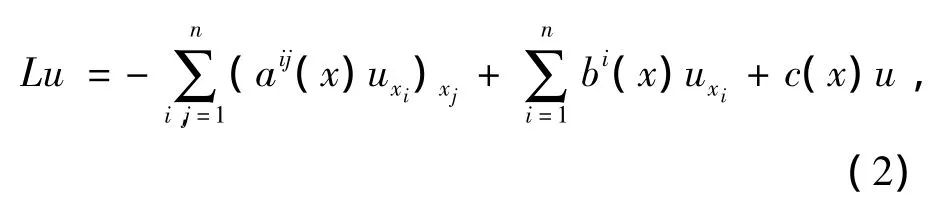
并且偏微分算子L是一致橢圓型算子，即存在常數θ＞0，使得:

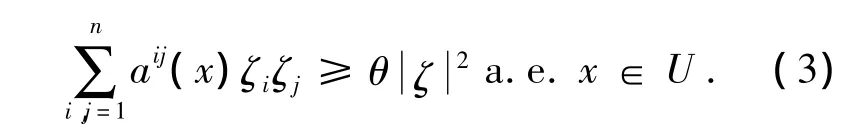
其中ζ∈Rn，并且對方程中的系數aij，bi，c進一步做出額外的假設.雙線性泛函B［，］是通過橢圓型算子L定義的，即:

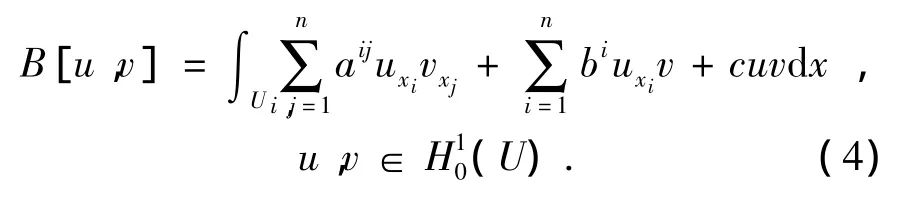
1 主要結果

本文的主要結論:

定理1 設m是一個非負整數，并且L的系數滿足:

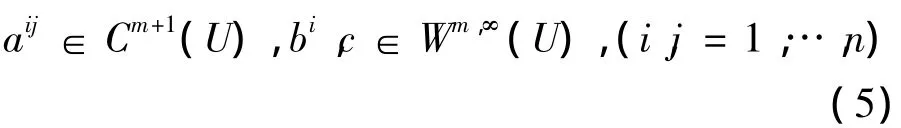
且

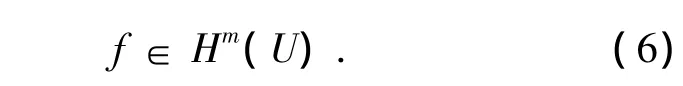
進一步假設u∈H1(U)是橢圓型方程Lu=f in U的一個弱解，則:

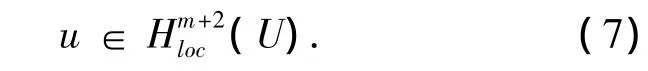
對于任意的V??U(即V是U的緊子集)，有:

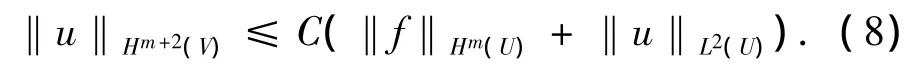
這里，常數C依賴于U，V及算子L的系數.

2 幾個要用到的結論

注意:在這里(，)代表的是 L2(U)上的內積.

定理2 設m是一個非負整數，并且L的系數滿足 aij，bi，c∈Cm+1(U)，f∈Hm(U)，如果 u∈H1(U)是橢圓型方程Lu=f in U的一個弱解，則u∈(U)且對于任意的V??U(即V是U的緊子集)有:

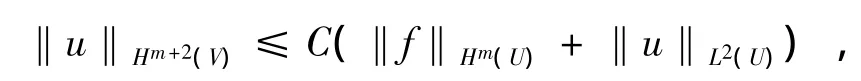
這里常數C依賴于U，V及L的系數.

注意:定理 2中要求 L的系數:aij，bi，c∈Cm+1(U)(證明的過程參考文獻［2］).在定理1中，我們對L的系數的范圍進一步放寬，只要求aij∈ Cm+1(U)，bi，c∈ Wm，∞(U)，則可得到同樣的結論.

3 定理1的證明

1)(7)、(8)結論的證明，我們采用歸納法.首先討論m=0的情況，即L的系數滿足aij∈C1(U)，bi，c∈ L∞(U)，f∈ L2(U). 如果 u ∈H1(U)是橢圓型方程Lu=f in U的一個弱解，則，且對于任意的V??U(即V是U的緊子集)，有

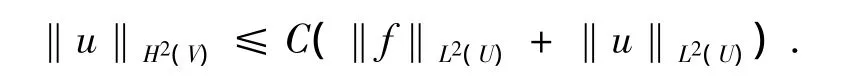
常數C依賴U，V及L的系數.

2)固定任意一個開集 V?? U，使得dist(?V，?U)= δ＞ 0(其中δ是一個常數)，選擇一個開集W，使得V??W??U，接著選擇一個光滑函數ζ(x)滿足:

在這里，ζ(x)為一個截斷函數(ζ(x)的取法見文獻［6］).

3)因為u是橢圓型方程Lu=f in U的一個弱解，?v∈(U)，B［u，v］ =(f，v).因此:

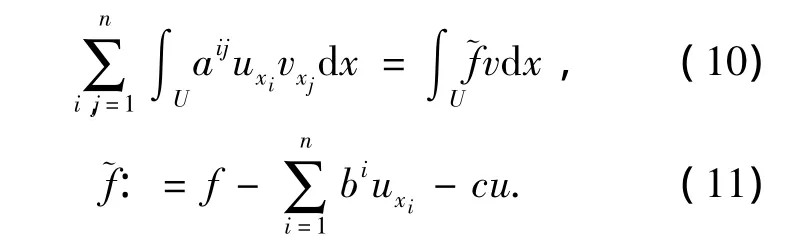
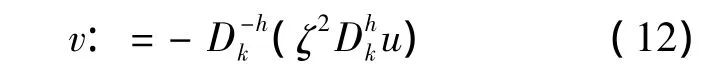
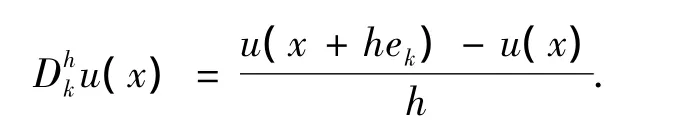
我們將表達式寫成:

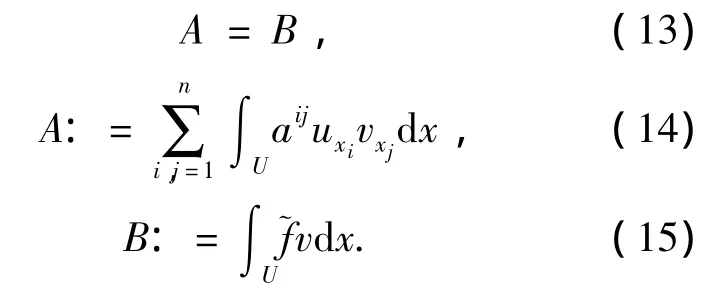
5)對A進行估計

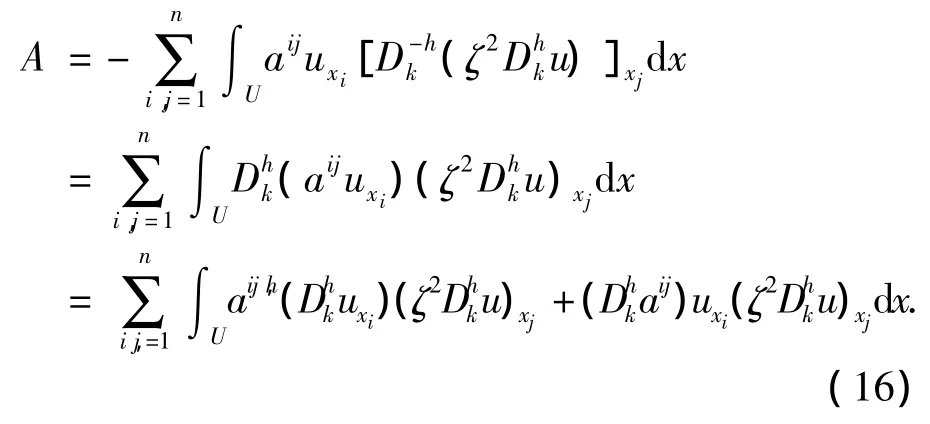
在這里用到的公式有:

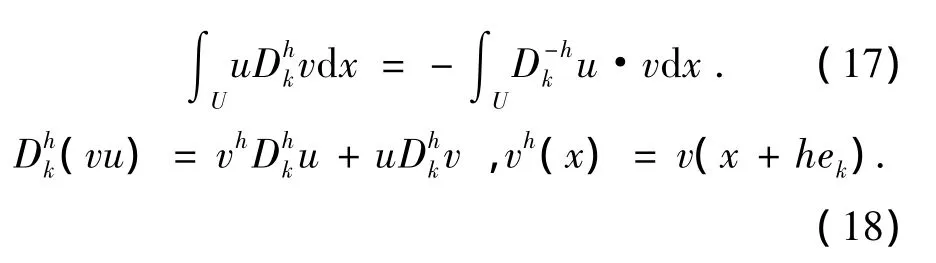
返回到(16)，我們發現:

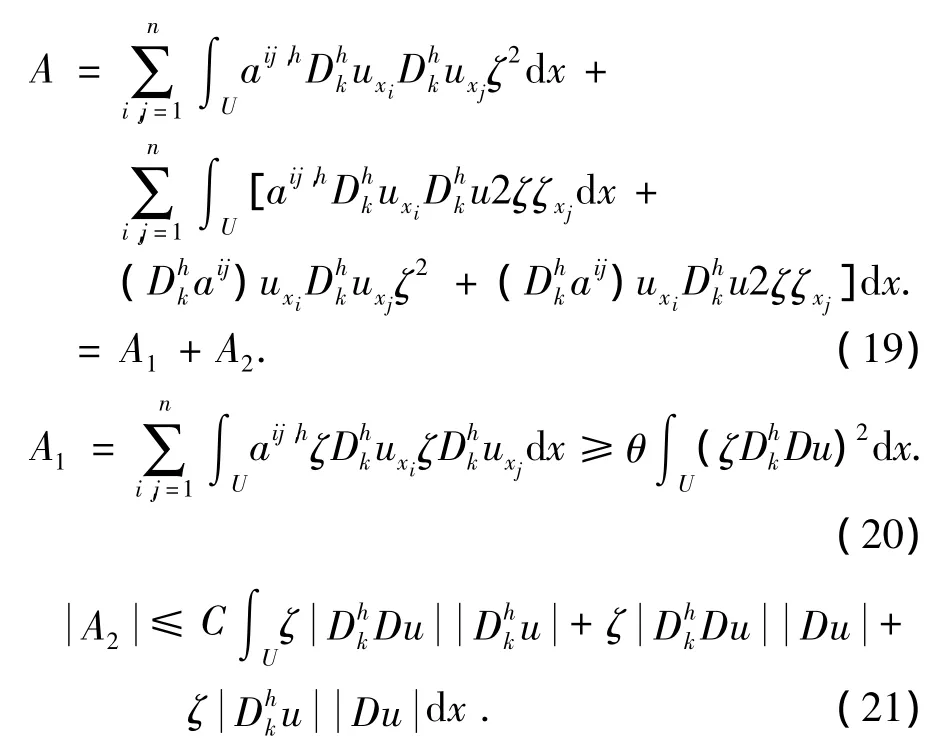
這里要求aij∈C1(U).

應用柯西不等式，整理得:

上式用到了(9)式中ζ(x)的定義.

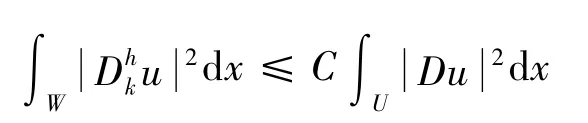
(見參考文獻［2］§5.8.2 中的定理3)

因此，可得不等式:

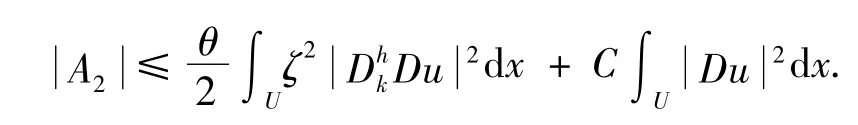
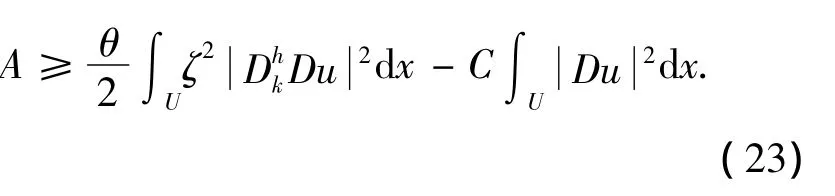
6)對B 的估計，綜合(11)、(12)、(15)得到:

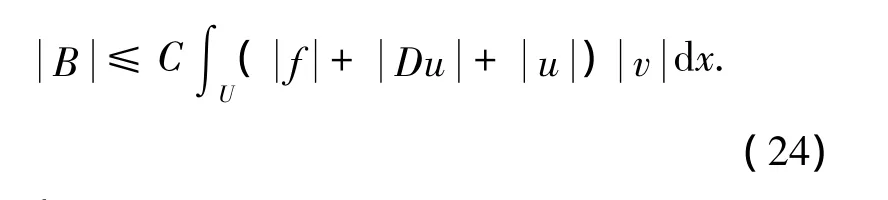
又因為:

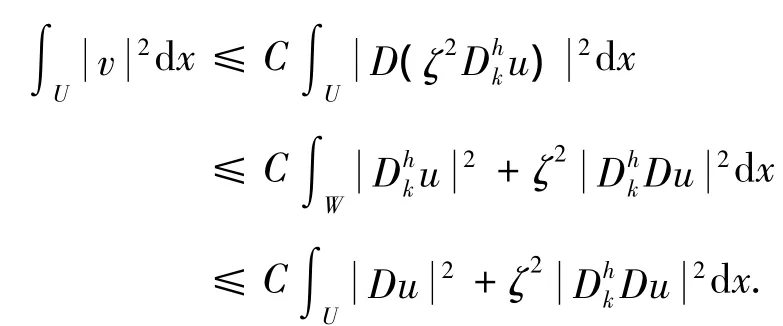
所以由ε的柯西不等式和(24)式得:

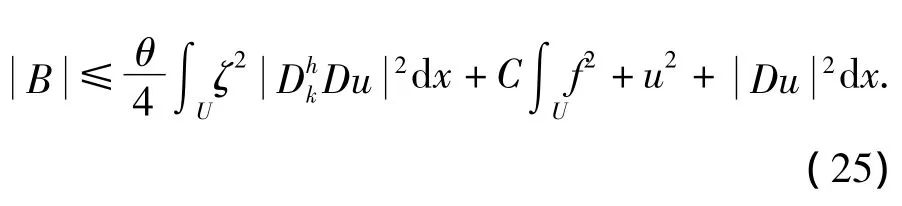
綜合(13)、(23)、(25)得:

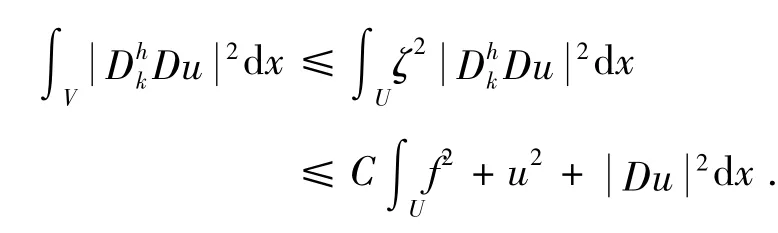
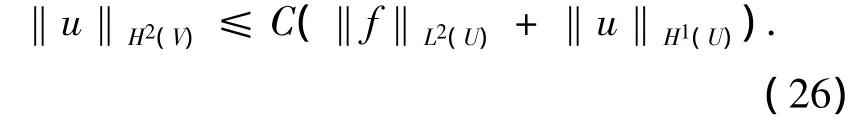
7)如果V??W??U，如同步驟2)～6)的方法可得:

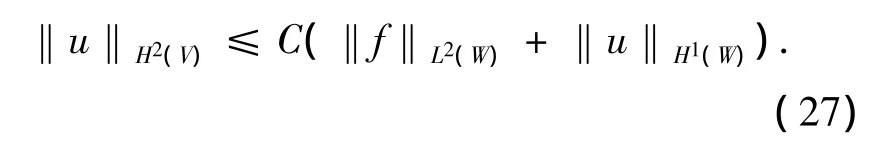
常數C與V，W及算子L的系數有關.

選取一個新的截斷函數:

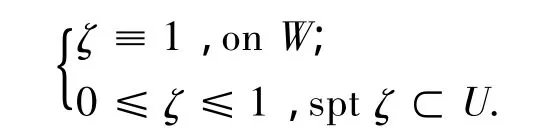
取v=ζ2u，則通過計算得:

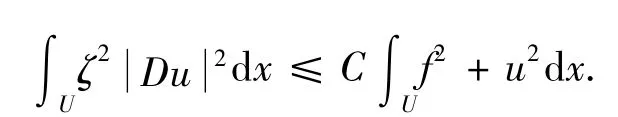
所以有:

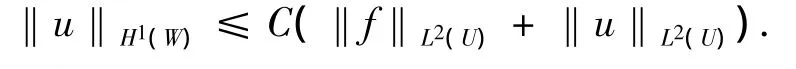
又綜合(27)式可得

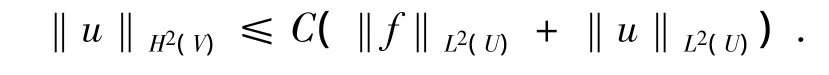
8)假設m=k+1(為一個非負整數)時結論成立.

9)那么當m=k+2時，即在aij∈Ck+2(U)，bi，c∈ Wk+1，∞(U)的假設前提下，同時 u ∈H1(U)是橢圓型方程Lu=f in U的一個弱解.

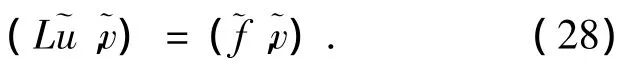
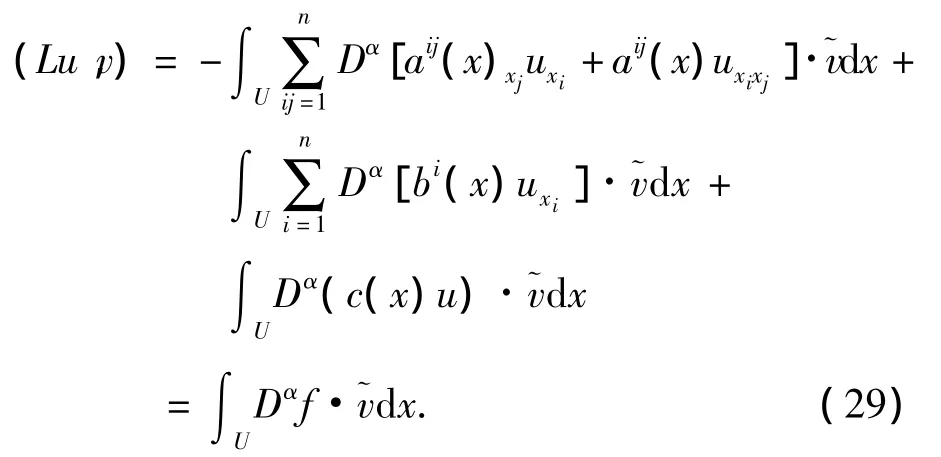
接著通過整理(29)式有:

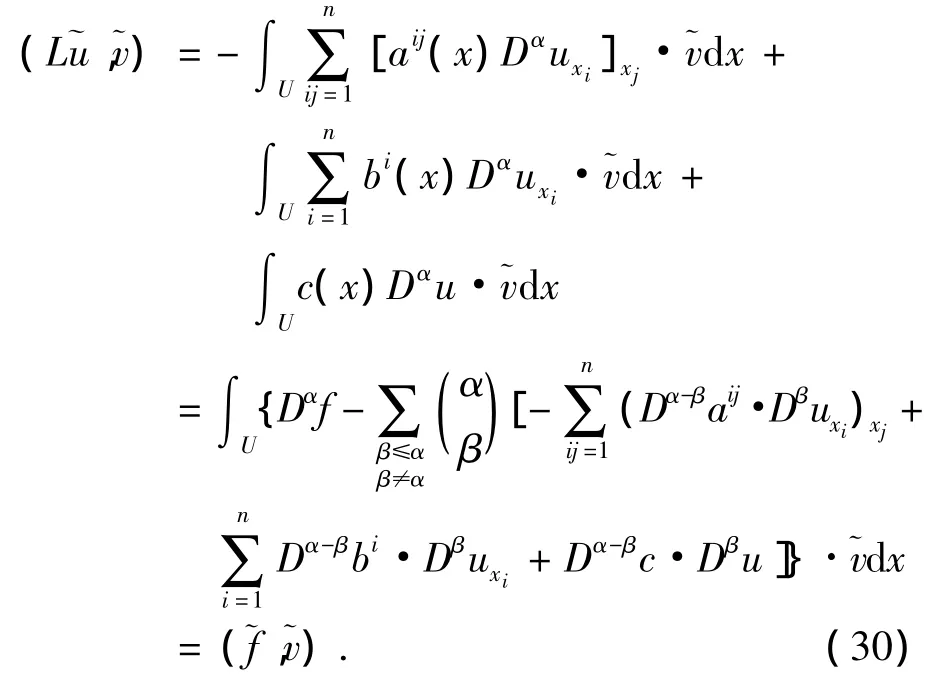
其中

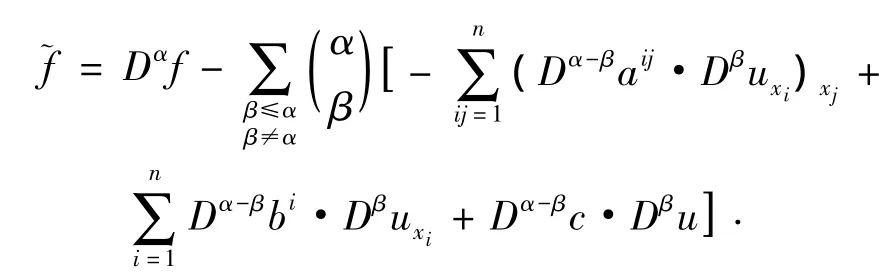
由弱導數的定義［6］，在中只要求:aij∈Ck+2(U)，bi，c ∈ Wk+1，∞(U)，就可得到 (L，)=).又結合步驟8)中的假設，我們可得到∈L2(W)且

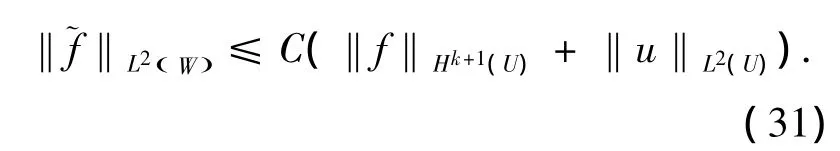
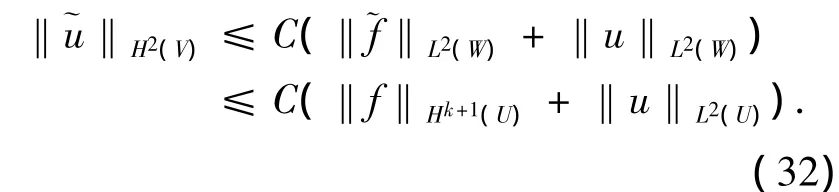
4 結論

在這篇文章中，我們對橢圓型算子L的系數范圍進一步放寬，只要求 aij∈ Cm+1(U)，bi，c∈Wm，∞(U)，并且函數u在邊界?U上不做出任何假設，然后通過一定的技巧和方法，討論了一類橢圓型方程弱解的內部正則性，給出了定理1的結論.

［1］李開泰，馬逸塵，王立周.廣義函數和 Sobolev空間［M］.西安:西安交通大學出版社，2008:67－83.

［2］Lawrence C Evans.Partial differential equations［M］.Rhode Island，1988:308－317.

［3］陳亞浙，吳蘭成.二階橢圓型方程與橢圓型方程組［M］.北京:科學出版社，1991:1－14.

［4］Zhang Yunzhang ，Yang Ganshan.Existence and regularity ofweak solutions for the biharmonic equation with complete second order derivative［J］.Dynamics of Continuous，Discrete and Impulsive Systems Series A:Mathematical Analysis，2010(17):215 －232.

［5］Lawrence CEvans.A survey of entropy methods for partial differential equations［J］.Bulletin AMS，2004，41(4):409－438.

［6］Walter rudin.Functional analysis:second edition［M］.劉培德，譯.北京:機械工業出版社，2004:23－57.

［7］Lin FH.On the Dirichlet problem forminimal graphs in hyperbolic space［J］.Inventiones Mathematica，1989，96(3):592－612.

［8］Daskalopoulos P，Hamilton R.Regularity of the free boundary for the 2 dimensional porousmedium equation［J］.JAmer Math Soc，1998，11(4):899 －965.

［9］Daskalopoulos P，Hamilton R，Lee K.All time c∞regularity of the interface in degenerated diffusion:a geometric approach［J］.Duke Math J，2001，108(2):295－327.