三角函數最值問題及其應用——例談高三數學第二輪復習的有效選題

211100 江蘇南京東山外國語學校高中部 柳發志 郭 俊

三角函數最值問題及其應用
——例談高三數學第二輪復習的有效選題

211100 江蘇南京東山外國語學校高中部 柳發志 郭 俊

高三數學第二輪復習的主要目標應是引導學生將所有高中數學知識和方法系統化、網絡化，熟悉知識間的聯系，掌握分析解決問題的一般思維方法，進一步領悟數學思想方法，明確“考什么”、“怎么考”，及時發現在前階段的復習中哪些知識點和方法技能掌握不牢固，哪些地方復習還不到位，做好查漏補缺、鞏固提升，第二輪復習一般以專題的形式，主干是解題訓練，以此提高學生的解題能力.顯然，學生解題能力的形成，并不取決于解題數量的多少，而與題目的質量有密切的關系，因此要想取得復習效益最大化，教師精選例習題顯得尤為關鍵，下面以“三角函數最值問題及其應用”這一專題談談筆者對第二輪復習有效選題的一些思考.

“三角函數最值問題及其應用”是高考中的重點考查內容之一，也是第第一輪復習的重點內容之一，那么第二輪復習中還應做些什么呢?應該說，此時的復習要做到減少與第一輪的重復，選題應重點突出，針對性強，注重知識的整合、方法的梳理，根據學生現狀，讓更多的學生感到有新意，有發展，有新收獲，從以上思考出發，對這一專題采用系列題組教學，引導學生比較鑒別，進行方法、規律的歸納總結.

鏈接 (2010南京高三模擬)如圖，現要在一塊半徑為1m、圓心角為60°的扇形紙板AOB上剪出一個平行四邊形MNPQ，使點P在AB弧上，點Q在OA上，點M，N在OB上，設∠BOP=θ，平行四邊形MNPQ的面積為S.

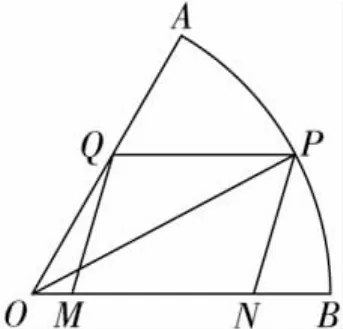
圖1

(1)求S關于θ的函數關系式;

(2)求S的最大值及相應的θ的值.

點評 本例是三角函數最值問題中的常規典型問題，本質是研究運用函數y=Asin(ωx+φ)性質，學生比較熟悉，選取此例指導學生扎實抓好基礎落實，熟練把握解題思路，注意思維嚴謹，在以三角函數為模型的一些應用題中，常常在得到類似函數解析式后求解最值，鏈接中的應用題源于教材，是此類問題的代表，高考中也常常出現.

點評 本例與例1形式上有相似之處，通過比較發現差異，解法上也有較大差異，這兒，視cosx為變量，聯想二次函數的性質，轉化為二次函數最值問題，通過此例，也提示學生注意題設條件，靈活選擇合適方法解題.

鏈接 (2008江蘇高考)如圖2，某地有三家工廠，分別位于矩形ABCD的兩個頂點A，B及 CD的中點 P處.AB=20km，BC=10km.為了處理這三家工廠的污水，計劃在矩形區域內(含邊界)且與A，B等距的O點建污水處理廠，并鋪設三條排污管道AO，BO，PO.記鋪設管道的總長度為ykm.

(1)按下列要求建立函數關系式：

(ⅰ)設∠BAD=θ(rad)，將y表示成θ的函數;

(ⅱ)設OP=x(km)，將y表示成x的函數;

(2)請你選用(1)中的一個函數關系式，確定污水處理廠O的位置，使三條污水管道的總長度最短.

點評 本例在形式上再次變化，出現了分式，教材中未曾出現，求解時就要求學生能站在高處看問題，通過解析式的適當變形，可視sinx+cosx為一整體，通過換元，轉化為一常見的分式形式的函數，可類比例2，但是如果解析式中兩分子的系數不相同，這時還這樣處理就比較困難了，因此，還可以將該函數視作一“普通的函數”，而不僅僅是“三角函數”，這時就聯想到可以運用導數工具，先通過導數方法研究這一函數性質，再運用性質求解最值，鏈接中的問題一般選用(i)中得到的函數求解比較方便，也體現了解題方法的優化.

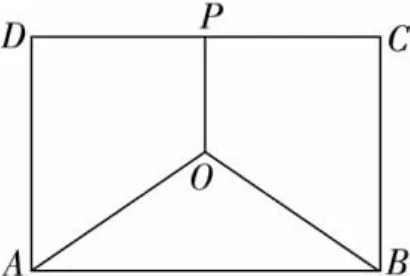
圖2

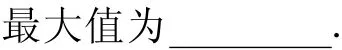
點評 本例在例3的基礎上再次變化，那么到底該選擇怎樣的解題思路與方法呢?注意到sin2x+cos2x=1及sin2x＞0，cos2x＞0，聯想到基本不等式運用中的常見問題，就有了解法.這兒更多的是引導學生善于觀察與發現，真正實現從數學運用的高度去思考，關注通性、通法，還要注意方法的優化.

對于這一專題為什么選用以上四例，下面再作簡要說明.

1 專題復習還應低起點，抓落實

從例1出發，雖說學生對此類問題比較熟悉，但在熟練程度上是否已達到要求，在第二輪中還需整固，通過觀察發現，明白解題根源，解題目標明確，能迅速將解析式進行變換轉化，這兒也對三角變換做回顧與檢查，另外，對題中出現角的范圍約束是否已引起注意并能用好該條件，通過本例應該說可以對三角變換及三角函數性質運用整體上作回顧與整合.

2 專題復習必須多比較，重方法

例1與例2形式上類似，但實際上差別很大，審題時是否出現誤讀?通過比較，

是否能將二次函數知識與三角函數知識串聯起來，快速合理切入解題?而到了例3、例4，又需要怎樣去分析判斷，怎樣合理選擇方法?這兒就要求學生能自覺從整個高中數學知識體系出發去思考問題解決方案，面對條件的變化，是否束手無策，能否克服困難?對學生的心理品質也提出要求.

3 專題復習必須成系統，高視角

1 石寅初.考試研究.南京：考試研究編輯部，2011，6

2 涂榮豹.數學之友.南京：數學之友雜志社，2010，4

20111128)