時域有限差分法分析混響室中場的均勻性

黃 華 牛中奇 白 冰

(西安電子科技大學電子工程學院,陜西 西安710071)

1.引 言

從眾多研究者的工作可知,混響室可采用多種數值方法進行仿真分析：矩量法(MOM)[1];時域有限差分法(FDTD)[2-6];有限元法(FEM)[7-8];FDTD與MOM混合法[9];FEM與FDTD混合法[10];平面波積分表示法[11];傳輸線矩陣法(TLM)[12]等。在經典的仿真分析中,建立的混響室模型一般由混響室的內部空間、攪拌器及天線三部分組成[13]。圖1所示即為混響室測試示意圖。

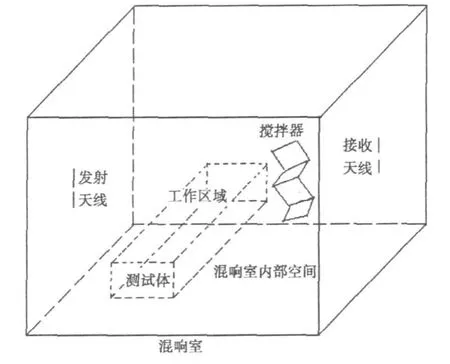
圖1 混響室測試示意圖

通常,仿真計算中耗費的時間與混響室的體積、六個壁面所用導體的電導率、電磁波的頻率范圍以及受試設備自身的特性有關,然而這會使得計算量很大,因而十分耗時,有時要用微機實現仿真幾乎是不可能的。為克服這一困難,Franco Moglie把重疊平面波理論[14]用到了該問題的處理之中,其基本思路是,用重疊平面電磁波替代經典仿真分析中當攪拌器轉動時產生的向不同方向傳播的電磁波,用在計算程序中設置的對源于不同方位的重疊波的重復計算次數等效經典仿真分析方法中的攪拌器的離散步進次數,而在相應的模型中只保留受試對象,如圖2所示。這樣便可模擬混響室內真實的電磁環境。然而,在該文獻中并沒有分析重疊入射波數目與混響室內場分布之間的相互關系,基于此,本文將對該問題進行研究,尋求其中的規律性以便為工程實踐提供理論指導。

圖2 隨機重疊入射平面波

2.方法簡介

2.1 隨機平面電磁波的生成

要把重疊平面波理論用于混響室內場的仿真分析,解決的關鍵問題是重疊平面波的生成。注意到攪拌器轉動時所產生的電磁波的傳播方向是隨機變化的這一特征,本文用所處方位是隨機的一組等效源產生的所謂隨機平面電磁波對其進行模擬。又由于本文將采用FDTD法對混響室內的場進行仿真計算,而在FDTD法中,入射波源是設置在總場區與散射場區的分界面即所謂的連接邊界面上的,因而,上述的一組等效源設置的具體位置應在連接邊界上。同時,構成這一組源的各個子等效源的位置參數及各個子等效源輻射的電磁參數在FDTD程序中應被設定,在每一暫態的迭代過程中只需調用即可。這些參數包括,每個子等效源在球坐標系中的坐標r、θ和φ以及由它們輻射出的電磁波的極化角α,即平面波的電場矢量與x軸的夾角,如圖3所示。圖中P點為一個子等效源所在點,E、H和n分別為由該等效源所產生的電磁波的電場、磁場和傳播方向的單位矢。為了模擬攪拌器轉動時所產生的電磁波的隨機性,設置在球坐標系中的一組等效源的分布方位亦應是隨機的,也就是說,一系列子波源設置點的方位角θ和φ是隨機的。但值得注意的是,θ和φ的隨機性要受到球坐標中坐標變量取值范圍的約束,同時在對θ和φ的隨機取值中還要防止等效源在某一區域內的分布過于集中,以致帶來對混響室內場隨機分布模擬的失實,因而,也要設置約束條件來予以防止,鑒于以上考慮,設置以下約束條件：

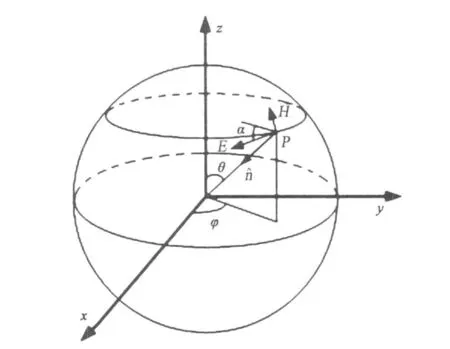
圖3 等效源的方位及其產生的電磁波的參數

1)θ的隨機取值應在[0,π]之間,以便滿足所用坐標系的約定。在此前提下,具體的隨機取值過程是,在 Fortran中首先由 random_element()在[0,1]之間抽取隨機數,然后再乘以π弧度即可得到一系列θ的隨機值。

2)φ的隨機取值應在[0,2π]之間,以滿足所用坐標系的約定。對φ的隨機取值中應特別值得注意的問題是,有時隨機取值的結果有可能出現某一區域的取值樣本過于密集,這種情況最有可能發生在高緯度即θ很小或θ很大的區域,對于發生這種情況的原因可作這樣的解釋：當θ很小或θ很大時,同球面上與之對應的緯度圈的周長2πrsinθ將很小,因而在取同樣數量的φ樣本個數的情況下,其樣本點的密度便遠大于其它緯度圈上的密度,因而若不加約束地按此種情況隨機設置等效源來模擬混響室內的場分布,其結果將嚴重失實。為此,給予φ的隨機取值附加了這樣的約束：令φ=ψ/(2×sinθ),對 ψ隨機取值,當ψ的某一隨機值使得與之相應的φ值落在[0,2π]之內,則保留之,否則則棄之重取,直至所取φ的個數滿足預設的等效源的個數為止。

3)α是線極化波的極化方向的表述,定義是電場矢量與x軸的夾角,稱其為極化角,其值在[0,2π]范圍內。設各等效源產生的電磁波的電場幅度均是1,即Em=1 V/m.

上述約束條件中,θ和ψ是兩個相互獨立的隨機取樣變量,其中約束條件2)是為了使所選取的一系列等效源分布點P不至于過分密地集中在球面的兩極附近,以便保證之后采用FDTD法時,設置在六個連接邊界面上的波源分布是較為均勻的,這樣才可較好地模擬在攪拌器轉動時所產生的電磁波的傳播方向是隨機的效果。

2.2 隨機平面電磁波的引入

在仿真分析中,一是要對電磁波的特性進行設置以模擬實際空間中實際存在的電磁波的特征,二是要把電磁波引入到仿真分析區域內的各點,以模擬電磁波在實際空間內的傳播。一般說來對電磁波進行設置的方法有兩種：一是解析方法,二是一維FDTD方法[15]。由于由一維FDTD方法引入的入射波在總場區內的分布較為均勻且在散射場區泄漏較小,故本文選用第二種方法。在下面的仿真分析中,由程序設置的是連續的正弦平面電磁波,為了使引入到各點的正弦波能夠快速地達到穩定,在開始的前半個周期加入了一個升余弦開關函數,而在后半個周期仍為正弦函數,如式(1)所示,其中,Em為電場振幅,f為電磁波的頻率,T為波的周期。

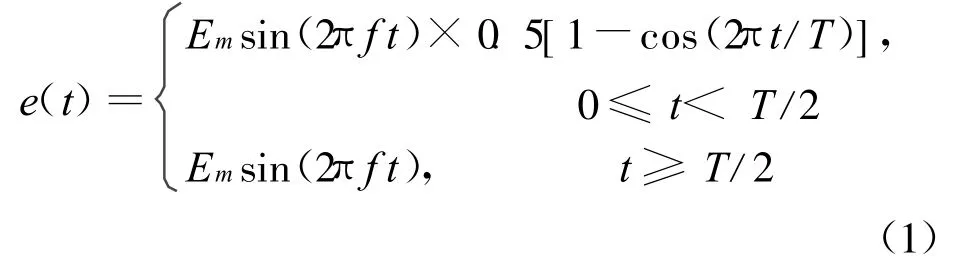
將Maxwell方程組中兩個旋度方程差分離散,再用一維FDTD法可得由電場表述磁場的如下表達式。

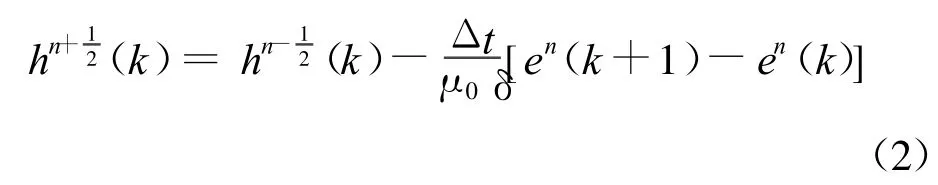
式中：μ0為真空中的磁導率;δ為討論空間的網格步長;Δt為計算中的時間步長;n為計算迭代的時間步數;k為空間網格的位置。

2.3 程序實現

本文用Fortran語言進行計算編程。下面對主要步驟予以簡介。

2.3.1 電磁波的引入

如2.2節所述,電磁波是采用一維FDTD法引入的,且對電磁波的種類及其表達式作了說明。現在介紹如何用Fortran程序予以實現。首先,在連續的正弦波上等間隔地采樣10000個,然后把這10000個樣本數據由一維FDTD法逐次推進到討論空間的每個網格內,每一時刻各網格內均占有10個采樣數據。這樣設置好后,再將由各個角度入射的波的傳播方向投影到直角坐標系的x、y、z方向上。當把如式(1)所示的、其參數Em、f和T為固定取值的、來至P1點等效源所產生的電磁波在混響室內的場分布計算完以后,再對入射波參數進行更新,即對P2點的等效源產生的電磁波在混響室內的場分布進行計算,直至把Pn點的等效源產生的場計算完畢。之后對場進行矢量疊加可得總場。

2.3.2 歸一化設置

由于同一電磁波的電場與磁場的振幅的數值之比為波阻抗,而對于空氣而言波阻抗η=377Ω,這表明,電場與磁場的量值不在同一數量級,為了在計算中獲得同樣的準確度,需對這兩個量進行歸一化處理[16],而當計算程序結束進行數據存儲時再將其還原。本文是對電場進行歸一化處理的,即程序處理時,令?E=E/η而H不變。另外,計算時,取討論空間中沿各坐標方向的步長相等,即Δx=Δy=Δz=δ,并令討論空間內的電導率σ=0,這樣Maxwell方程離散式前的系數就只剩下了 Δt/(ε0δ)和Δt/(μ0δ)兩項。由于

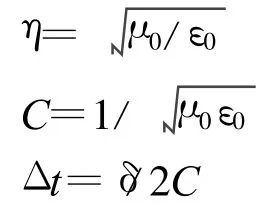
故有

將式(4)代入式(2),有

若將上式中的因子[en(k+1)-en(k)]/η記為(即歸一化為),則式(5)可寫為

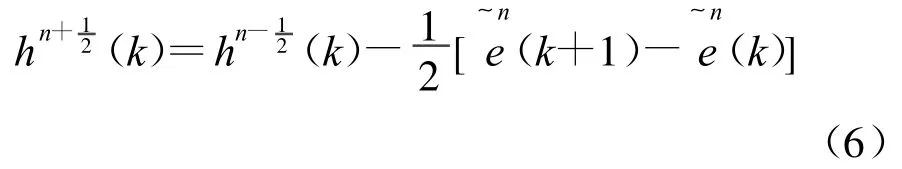
將其它的離散式進行同樣的處理。再將歸一化電場?E=E/η代入式(1),有

上面是對電場歸一化處理的具體步驟,存儲數據時再用E=η?E對電場進行還原。當然,在方法上也可將磁場歸一化為?H=ηH而E不變,處理后可得與上述類似的表達式,只是在數據存儲時需對磁場進行還原。

3.仿真計算及結果分析

作為有實際背景的事例,計算中將討論空間的網格數取為90×90×90,其中沿各坐標方向,連接邊界與吸收邊界的距離為10個網格。取電磁波頻率為915 MHz;空間步長為0.025 m;時間步長為Δt=4.5×10-11s,Δt這樣的取值是為了滿足數值穩定性的要求。對計算數據的最終處理是將由Fortran程序計算出的數據導入Matlab程序中完成的。

3.1 對平面電磁波正弦特征的檢驗

2.2節中已經說過,在本文中由程序設置連續平面正弦電磁波以對在正弦電磁波隨機入射時混響室內的場分布進行仿真,但為了使推進到各網格的正弦波快速地達到穩定狀態以滿足仿真要求的條件,因而作了式(1)那樣的處理。那么這樣處理之后電磁波還會保持正弦電磁波那樣的特點嗎?這就需要檢驗。圖4和圖5分別為當將正弦電場和磁場離散為200個取樣點后,再用式(1)處理的結果。由圖可以看出,其波仍保持著好的正弦特征,且電場幅度和磁場幅度之比正好等于波阻抗。

3.2 隨機入射平面電磁波的等效源分布

本文中,分別將產生隨機入射正弦平面電磁波的等效源的個數設置為 1、10、20、100、200 、300、400和500個,以便從結果中看出場分布與源的個數間的關系。在此,僅將源為500個時它們在球面上的分布示于圖6中。當然,對它們具體位置的設置是按照2.1節中的約束條件選取的。其中,圖6(a)為觀察者位于球坐標θ=28°,φ=60°處的俯視圖,圖6(b)為觀察者位于θ=32°,φ=23°處的俯視圖。

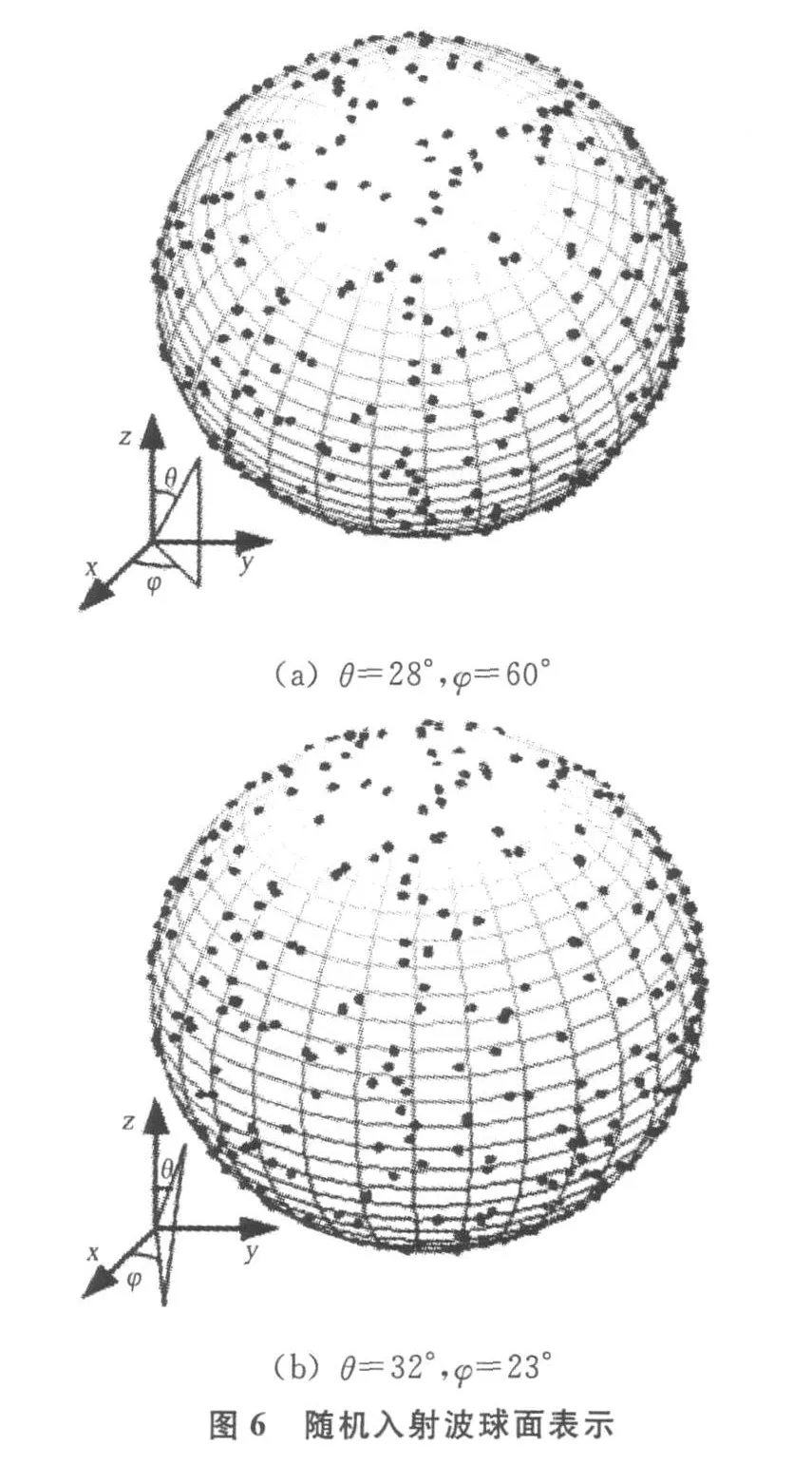
從圖中可以看出,波源在球面上的分布是隨機均勻的,是滿足統計規律要求的。

3.3 混響室內場分布仿真及數據分析

在此,以對尺寸為2.1 m×2.3 m×3.5 m的混響室的工作區域按90×90×90個網格劃分后進行場分布仿真計算為例。對該區域內場的均勻性與哪些因素有關進行討論。具體做法是,分別選擇隨機入射電磁波的個數為 1、10、20 、100 、200 、300 、400 和500個,計算區域內不同剖面層中的場分布,其結果以圖示形式給出。限于文章篇幅,文中僅給出了yoz平面內的第45層,xoz平面內的第56層和xoy平面內的第68層的電場分布于圖7的(a1)→(h1),(a2)→(h2)和(a3)→(h3)中。圖中N表示重疊入射波的個數,網格從1→10、80→91代表吸收邊界到連接邊界的網格數。在yoz、xoz和xoy三個平面中的第45層、第56層和第68層的這三個層面是任意選取的。

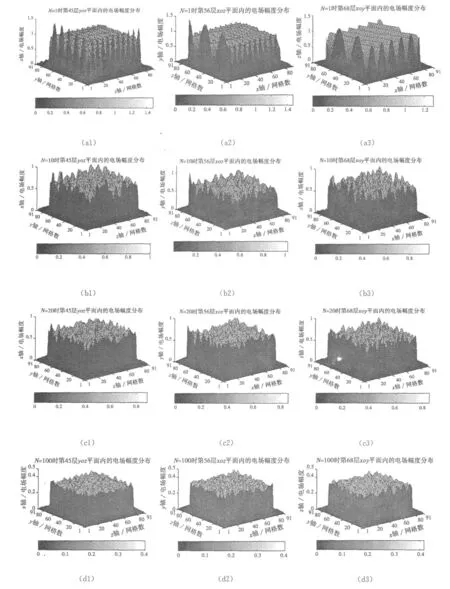
其中層數的劃分是對90×90×90的計算區域進行的,每個坐標方向上均可化為90層,如圖8所示,虛線正方體為計算區域。

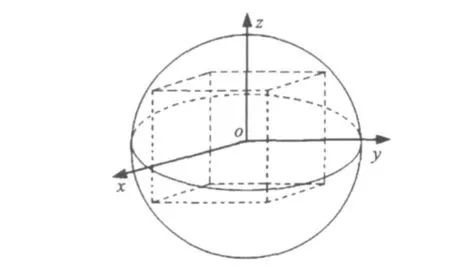
圖8 計算區域層數劃分示意圖

基于上述仿真結果并按照IEC61000-4-21標準中規定的計算方法就可以計算出混響室工作區域中的場均勻度,如表1所示。當入射波的個數為1時,電場強度的標準偏差為3.40 dB,它不滿足標準中所提出的3 dB要求,并且可從圖7的(a1)、(a2)和(a3)直觀看出,此時場均勻性較差,它們的電場強度起伏較大,且包絡為正弦規律,這就說明單個波入射的情況下混響室內場的均勻性較差;但隨著入射電磁波數目的增加,比如,當入射波的個數大于或等于10時,標準偏差在小于3 dB的前提下逐漸減小,這表明場的均勻性越來越好,但與此同時,計算時間亦會逐漸增加,對計算機硬件的要求也同步提高。因此,對那些復雜的、要求精度高的問題在單個計算機不能處理或其消耗的時間相當長的情況下可采用并行算法進行求解。上述結果也提示人們,在對研究對象進行數值分析之前必須要依據問題的復雜性及其求解的精度要求,適當地選取入射波的個數,以達到既節約計算時間又滿足求解精度的目的。

表1 頻率為915 MHz時場的均勻性隨入射波個數的變化

4.結 論

把重疊波理論運用到混響室的仿真分析中,使得計算時間只與測試體的特性相關,這樣不僅能使仿真過程中混響室內的電磁環境與實際混響室內的電磁環境更接近,而且與傳統的混響室仿真分析相比還可以大大縮短計算時間;同時,分析比較了不同重疊入射平面波情況下混響室內場分布的均勻度,得出了欲使混響室內場分布達到預設均勻度要求時,所應選取的最佳重疊入射平面波的數目,而本文工作中所表明的混響室內這種場分布的預期精度與應選取重疊入射平面波個數間的關系是文獻[14]沒有提及和體現的,從而為混響室的設計提供了可靠的理論指導。

[1] LEGNAB T,FREYER G,HATFIELD M,et al.Verification of fields applied to an EUT in a Reverberation chamber using numerical modeling[C]//IEEE Int.Symp.Electrom.Compatibility,1988,1：28-33.

[2] BONNET P,VERNET R,GIRARD S,et al.FDTD modeli-ng of reverberation chamber[J].Electronics Letters,2005,41(20)：1101-1102.

[3] BAI L,WANG L,WANG B,et al.Reverberation chamber modeling using FDTD[C]//IEEE Int.Symp.Electromagn.Compatibility,1999,1：7-11.

[4] CHUNG S Y,RHEE J G,RHEE H J,et al.Field unitormity characteristics of an asymmetric structure reverberation chamber by FDTD method[C]//IEEE Int.Symp.Electromagnetic Compatibility,2001,1：429-434.

[5] HARIM A K.FDTD analysis of electromagnetic fields in a reverberation chamber[J].IEICE Trans.Communication,1998,E81-B(10)：1946-1950.

[6] KOUVELIOTIS N K,TRAKADAS P T,CAPSALIS C N.Examination of field uniformity in vibration intrinsic reverberation chamber using the FDTD method[J].Electro.Letters,2002,38(3)：109-110.

[7] BUNTING C F.Statistical characterization and the simulation of a reverberation chamber using finite-element techniques[J].IEEE Trans.Electromagnetic Compatibility,2002,41(1)：214-221.

[8] BUNTING C F,MOELLER K J,REDDY C J,et al.A two-dimentional finite-element analysis of reverberation chambers[J].IEEE Trans.Electromagnetic Compatibility,1999,41(4)：280-289.

[9] HOEPPE F,GINESTE P,DEMOULIN B,et al.Numerical predictions applied to mode-stirred reverberation chambers[C]//Proc.Reverberation Chamber,Anechoic Chamber and OATS Users Meeting.Seattle,WA,2001.

[10] SURIANO C R,THIELE G A,SURIANO J R.Low frequency behavior of a reverberation chamber with monopole antenna[C]//IEEE Int.Symp.Electromagnetic Compatibility,2002,2：645-650.

[11] HILL D A.Plane wave integral representation for fields in reverberation chambers[J].IEEE Tran.E-lectromagnetic Compatibility,1998,40(3)：209-217.

[12] PETIRSCH M,SCHWAB A J.Investigation of the field uniformity of a mode-stirred chamber using diffusers based on acoustic theory[J].IEEE Transaction electromagnetic Compatibility,1999,41(4)：446-451.

[13] 沈遠茂,石 丹,高攸綱,等.利用多天線源攪拌改善混響室場均勻性的分析[J].電波科學學報,2009,24(4)：682-686.SHEN Yuanmao,SHI Dan,GAO Yongang,et al.Improvement in field uniformity introduced by multiple-antenna in source-stirred reverberation chamber[J].Chinese Journal of Radio Science,2009,24(4)：682-686.(in Chinese)

[14]MOGLIEF,PASTORE A P.FDTDanalysis of plane wave superposition to simulate susceptibility tests in reverberation chambers[J].IEEE Trans.Electromagn.Compatibility,2006,48(1)：195-202.

[15] 葛徳彪,石守元,朱之偉.一種新的FDTD入射場設置方法[J].微波學報,1995,11(3)：187-190.GE Debiao,SHI Shouyuan,ZHU Zhiwei.A new FDTD scheme for introducing incident fields[J].Journal of Microwaves,1995,11(3)：187-190.(in Chinese)

[16] 葛德彪,閆玉波.電磁波時域有限差分方法[M].西安：西安電子科技大學出版社,2005：14-20.