基于模糊神經網絡的環管反應器故障診斷

閆志國，鄭 明，宣愛國，吳元欣

(武漢工程大學 綠色化工過程省部共建教育部重點實驗室湖北省新型反應器與綠色化學工藝重點實驗室，湖北 武漢 430073)

環管反應器是丙烯聚合工藝中的一個重要組成部分，該系統影響參數多、相關設備多且大多處于高溫高壓的工作環境，其故障發生率高、危害較大。傳統的定時、周期性維修很難滿足安全生產的需要，人工智能方法實時檢測環管反應器運行設備參數，可根據各種參數的異常變化對系統進行故障預測與診斷，為設備的長時間平穩運行提供安全依據。

模糊神經網絡(Fuzzy neural network，FNN)故障診斷方法通過對環管反應器運行流程的分析研究，提取故障及其征兆，結合模糊數學知識建立隸屬函數來描述故障及征兆信息并進行推理，再借助神經網絡對模糊信息進行自學習、分析，建立一定的信息診斷規則系統，在此基礎上輸入征兆信息進行計算即可得到正確的故障診斷結論。

1 模糊神經網絡原理與結構

模糊神經網絡故障診斷是一種將模糊數學理論和人工神經網絡理論相結合的故障診斷方法。在模糊數學基礎上建立模糊推理邏輯，通過隸屬函數的方法，結合環管反應器系統運行的專業知識理論，建立滿足人工神經網絡軟件輸入輸出的故障征兆知識庫。人工神經網絡軟件通過調用知識庫中的知識進行學習，建立滿足系統故障處理要求的神經網絡，進行故障信息的分析和處理，得到正確的故障診斷結論。

1.1 模糊神經網絡原理

化工生產過程中故障與征兆之間并沒有嚴格的定量或邏輯因果關系。對同一故障，可能會產生多種征兆；同一種征兆，可能對應有多種故障存在。基于模糊數學知識的模糊集表示的模糊變量語言能夠更加準確地表示具有模糊特性的征兆和故障，符合事物的客觀本質，還能處理診斷過程中的不完整信息和不確定信息；神經網絡具有處理復雜多模式及進行聯想、推測及記憶的功能，具有自組織學習、自學習能力。融合了二者優點的模糊神經網絡技術就更加顯現出了這種特性[1]。

假定考察一個系統的3種故障類型：y1=故障1、y2=故障2、y3=故障3，于是構成了故障集合Y={y1，y2，y3};故障征兆分為：x1=征兆1、x2=征兆2、x3=征兆3，構成了征兆集合X={x1，x2，x3}。

設經過模糊數學處理，對于故障類型征兆(x1)1的影響因素為70%、征兆2的影響因素為20%、征兆3的影響因素為10%；則有對x1的診斷向量為(0.7，0.2，0.1)、對x2為(0.3，0.4，0.3)、對x3為(0.3，0.3，0.4)。

于是得到一個故障與征兆的關系矩陣：

對于不同類型的故障，各個征兆因素的影響權重不同。假設某類征兆對故障的影響權重A=(0.5，0.3，0.2)，則，由模糊合成運算可得到故障診斷向量(B)如下：

=(0.5，0.3，0.3)

式中，·表示模糊算子。

根據隸屬度最大原則，可知在權重A的影響下對于這類故障集最可能的影響因素是x1，即征兆1[2]。

基于模糊神經網絡故障診斷的步驟一般如下：

(1)利用模糊數學知識將提取的故障征兆信息模糊化處理，處理后的數據要滿足神經網絡的輸入輸出要求，同時要確保數據具有較好的精確度；數據一般分成訓練樣本、檢驗樣本和測試樣本3部分。

(2)利用處理后的數據對神經網絡進行訓練，以獲得比較合適的神經網絡模型。主要依據運算得到的實際輸出與目標輸出之間的誤差，較小則滿足設計要求。

(3)利用檢驗數據來檢測神經網絡模型的性能和泛化能力；進一步修正網絡直到模型性能達到要求。

(4)輸入測試樣本進行故障診斷。

1.2 模糊神經網絡結構

4層模糊神經網絡結構如圖1所示。

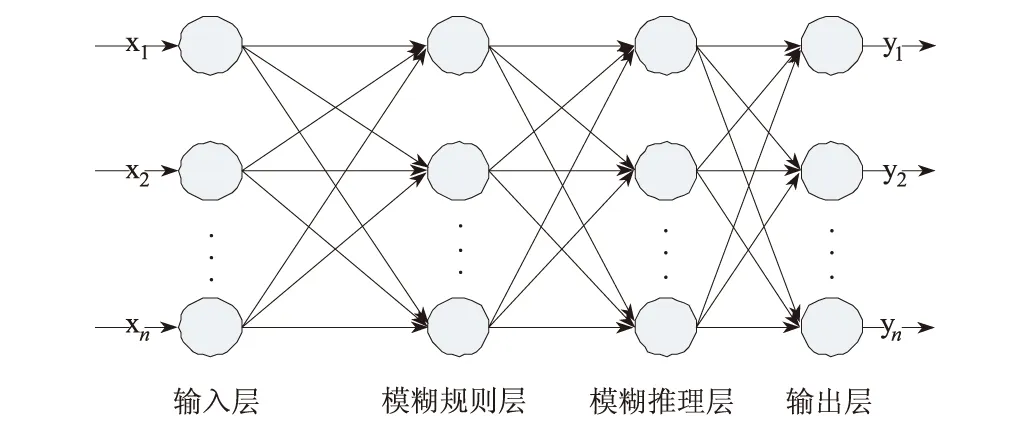
圖1 模糊神經網絡結構

模糊神經網絡的第1層為輸入層。輸入層的每個神經元對應一個輸入變量，直接將輸入數據傳給第2層神經元。

第2層為模糊規則層。該層完成從特征信號向滿足網絡輸入模式之間的轉化，即將故障征兆變量信號轉化為以隸屬函數表示的模糊變量。

第3層為模糊推理層。該層應用神經網絡算法完成推理診斷。

第4層為輸出層。該層將第3層的數據進行清晰化輸出，根據輸出向量的隸屬度來確定故障原因。各輸出節點輸出模糊數值大小代表該故障發生的可能性。

2 模糊理論對故障的表述

2.1 丙烯聚合環管反應器溫度升高時故障征兆提取

通過對丙烯聚合環管反應器溫度升高的故障機理進行分析，得到了環管反應器溫度升高的故障原因及其征兆參數變化樣本集，見表1。

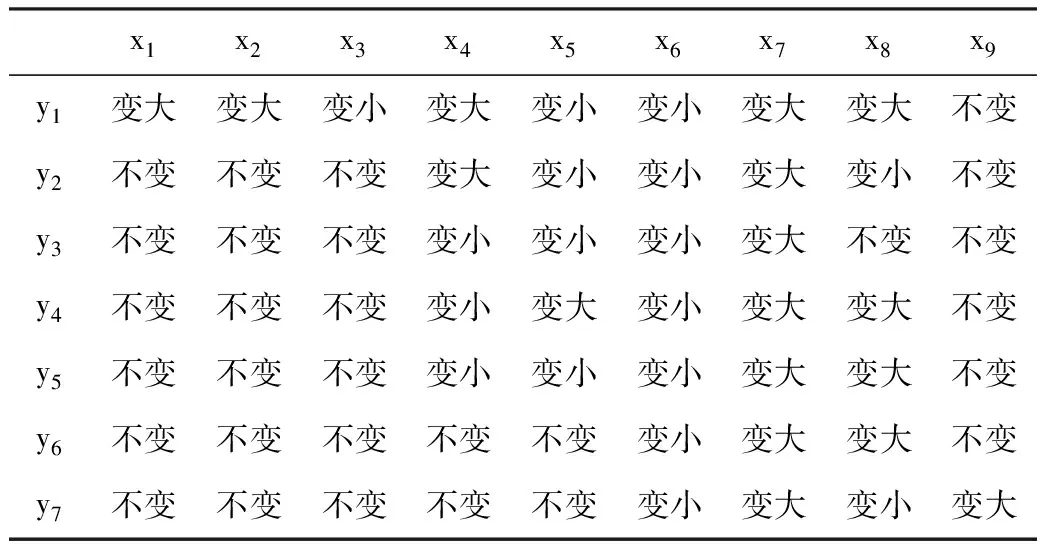
表1 環管反應器溫度升高時故障及其征兆參數變化

2.2 模糊邏輯推理

模糊邏輯推理是在模糊數學理論基礎上，通過隸屬函數的方法，結合環管反應器設備運行的專業理論，建立故障及征兆知識庫。模糊邏輯推理中最重要的環節是隸屬函數的確定。隸屬函數就是根據環管反應器設備運行的影響因素(即征兆參數)對反應器設備的影響程度，來確定主要故障的自定義函數。常用的隸屬函數形式有三角形函數、梯形函數、柯西函數和正態函數等。由于正態函數比較光滑平穩，結合環管反應器設備運行情況，在此選用正態函數來表示故障及其征兆的隸屬函數[3，4]。

結合環管反應器設備的典型故障及其征兆所具有的特點，設a為被測參數的下限值；b為被測參數的上限值。對于單向變大的參數，a為保證機器正常運行的最低測量值；對于單向變小的參數，b為機器正常運行的最大測量值；對于雙向波動的參數，a為保證設備正常運行的最低限值，但大于最低測量值，b為保證設備正常運行的最高限值，但小于最大測量值。

對于單向變大參數，隸屬函數設為：

當x=b時，有f(b)<0.9，求得k(b-a)2<4ln10，為計算方便取k(b-a)2=10，代入函數式得:

對于單向變小參數，隸屬函數設為：

當x=a時，有f(a)<0.1，求得k(a-b)2<4ln10，為計算方便取k(a-b)2=10，代入函數式得:

對于雙向波動變化參數，隸屬函數設為：

同上方法該函數中有f(a)=f(b)<0.1，化簡得函數:

2.3 模糊神經網絡訓練樣本的確定

結合故障發生時參數的變化值可以得到神經網絡訓練樣本輸入數據和輸出數據及其對應故障原因。結果見表2、表3。

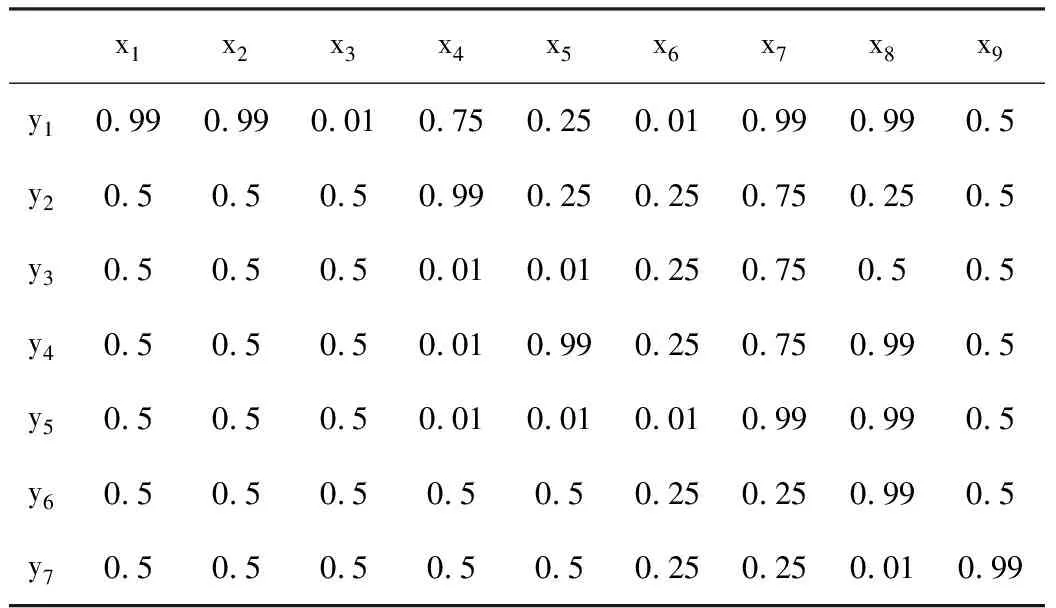
表2 神經網絡訓練樣本輸入數據

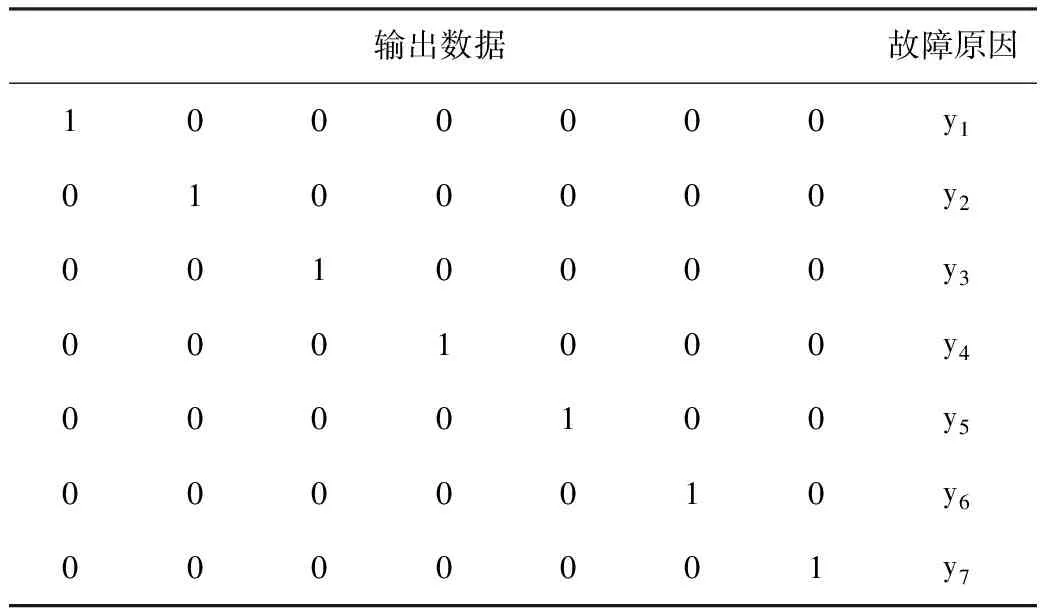
表3 神經網絡訓練樣本輸出數據及對應故障原因

表2中所取數據經Matlab中的模糊邏輯工具箱驗證，具有較高的準確性。

3 神經網絡設計

對于模糊化訓練樣本集，本系統選用BP神經網絡進行學習訓練。BP網絡的設計，一般從網絡層數、各層神經元個數、初始權重值及學習率等的選取進行考慮。

3.1 網絡層數及各層神經元個數的確定

3.2 初始權重值及學習率的確定

由于BP網絡系統具有非線性的特點，初始權重值的選擇一般影響函數能否達到局部最小、是否收斂及訓練時間的長短等。一般條件下，單獨訓練BP網絡時，初始權重值的選擇范圍為(-1，1)之間的任意數。

神經網絡的學習率直接影響每次訓練權重值的變化量。大的學習率導致系統不穩定，小的學習率不能保證網絡的誤差值趨向最小誤差。因此，一般選擇比較小的學習率來保證網絡的誤差最小，其取值范圍為(0.01，0.8)之間的任意數值[6]。在此學習率取值為0.01。

在獲得神經網絡輸入輸出數據及設定各種訓練參數之后，直接在Matlab7.0中Command Windows界面進行編程或借用Mmatlab7.0自帶的神經網絡工具箱(Nntool)進行訓練，得到滿足計算需要的模糊神經網絡，將其存儲以供故障診斷時使用。

4 故障診斷實例

隨機采用環管反應器發生故障時的現場參數運行數據，利用上述的正態函數進行模糊化處理，得到2組數據，如表4所示。

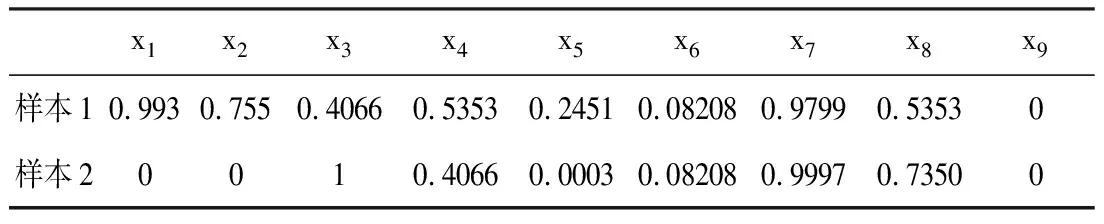
表4 神經網絡故障診斷輸入數據

將表4中數據輸入模糊神經網絡中進行計算，對應得到2組數據，如表5所示。

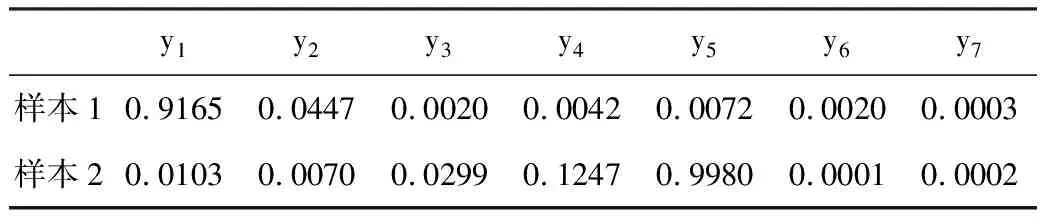
表5 神經網絡故障診斷輸出數據

依據模糊隸屬度最大原則及表5可知，在樣本1和樣本2數據描述的參數變化下，最有可能產生的故障類型分別為y1(進料系統故障)和y5(夾套水循環泵故障)，與丙烯聚合現場故障記錄相同。表明本方法是切實可行的。

5 結論

針對環管反應器發生故障時其故障征兆參數變化的復雜性、模糊性，采用模糊神經網絡的方法進行故障診斷。故障診斷實例表明，基于模糊神經網絡的故障診斷方法結合了模糊理論和神經網絡的優點，容錯力強、診斷速度快，能夠準確地診斷丙烯聚合環管反應器的典型性故障。

[1] 陳意，王軍，高占勝，等.基于分布式模糊神經網絡的船舶機電故障診斷[J].中國航海，2008，31(1)：49-51，74.

[2] 朱劍英.智能系統非經典數學方法[M].武漢：華中科技大學出版社，2001：156-168.

[3] 吳志鋼，林中達.基于模糊神經網絡的凝汽器故障診斷系統[J].燃氣輪機技術，2008，21(1)：42-45.

[4] 黃政淳，張德政.模糊神經網絡在破碎機故障診斷系統中的應用[J].微計算機信息，2006，22(7)：207-208，206.

[5] 王正武，張瑞平.基于神經網絡的故障模糊診斷研究[J].系統工程學報，2005，20(3)：300-334.

[6] 周強.基于模糊神經網絡和遺傳算法的故障診斷方法研究[D].大連：大連理工大學，2004.