GNSS－R反演海浪有效波高實驗分析①

楊 堯，李明里，李偉強，楊東凱

（北京航空航天大學，北京100191）

0 引 言

海浪有效波高（SWH）是海況探測中的重要一項，在相關領域中起著重大作用。傳統的探測有效波高的手段利用衛星高度計探測和高頻地波雷達探測。

近年全球衛星定位系統（GNSS）發展迅速，不僅為用戶提供了導航定位和精確授時信息，還提供了全天時不間斷的L波段微波信號資源。研究表明，GNSS反射信號可應用于遙感應用。其技術原理是利用導航衛星L波段微波信號為發射源，通過航空或衛星平臺上搭載的 GNSS－R（GNSS－Reflection）接收裝置，全天時、全天候進行導航衛星直射及反射信號的同步接收，通過對直射和反射信號進行處理實現海洋要素微波遙感探測［1]。基于全球衛星定位系統的GNSS－R海洋微波遙感技術成為當前倍受關注的熱點。

GNSS－R技術也可用于海浪波高探測。目前，基于GNSS－R技術的有效波高探測方法有兩種。其一為利用海面回波信號的一維時延相關函數微分函數的探測方法［2]：由于海浪的存在，海洋表面粗糙，造成電磁波的漫反射，使得鏡面反射得到的相關結果峰值上疊加了不同的延遲相關結果峰值，使最大的反射相關峰值后移，相關峰值的形狀也發生了變化。回波功率的斜率隨著海浪高度的分布而變化，因此，從DCF函數中可以得到海況信息。從DCF峰值的高度可以得到海面風速，從DCF函數的峰值點的碼延遲位置可以得到海面平均高度，從DCF函數的寬度可以得到海面大浪的高度［3]。由于這種方法目前還沒有具體實施方法，只是在理論上分析其可能性，因此，本文不作詳細敘述。另一種方法是利用干涉復數場（ICF）測算海浪有效波高。本文對ICF方法進行分析討論，并利用采集的數據對此方法進行分析。

1 利用干涉復數場測算有效波高

采用的接收機輸出為直射和反射信號的復數時間序列，被稱為零級數據。這個零級數據可以用于獲得一級數據，如下面將要涉及的干涉復數場，信號的相關功率等，再利用一級數據就可以獲得接收機與反射面高程差，有效波高，風速等二級數據。當然，軟件接收機同時也能輸出相應的導航信息，這里不詳述。

1.1 干涉復數場

干涉復數場（ICF），是本文測量有效波高的重要信息。它定義如下［3－4]：在時間t時，干涉復數場為

其中，FD和FR分別表示直射和反射信號復數波形的最大幅度的復數值。

直射信號在這里用作一個參考信息，用來消除與海洋運動無關的項，例如一些殘余多普勒頻偏，導航比特相位偏移和直射信號功率變化以及絕大部分由電離層和中性大氣引起的附加時間延遲對后續相關分析的影響。有效提高了測量海況信息的精度。ICF函數包含非常有價值的海況信息［3]。

相干積分濾掉了ICF函數的高頻分量，在探測遠海海況時需要考慮這一因素［3]。因為本文數據利用岸基接收機采集，所以不考慮該因素。

1.2 ICF的相關時間

需要重點討論ICF函數的相關時間τF，定義ICF自相關函數的時間寬度Γ（Δ）［3－4]：

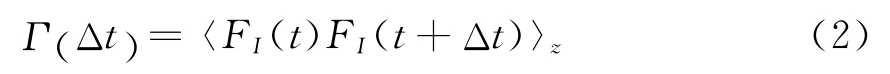
設海面高度為一個高斯概率分布，在這種情況下，相關時間和波浪方向無關。這樣，ICF的相關時間可作為該高斯函數的二階矩［3－4]：

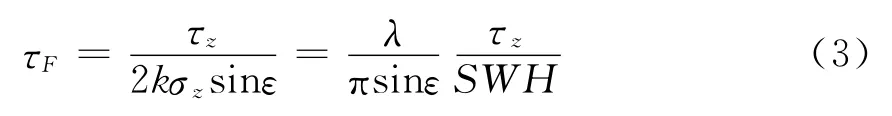
可以看出，τF依賴于表面相關時間，有效波高的比值以及波長。

1.3 有效波高（SWH）反演模型

在遠海海域，海浪可以充分成長，因此，可以根據海浪譜推導海面相關時間和SWH之間的關系式。Soulat等基于Elfouhaily等提出的統一海浪譜推導了τF和SWH 之間的關系式，是一個半經驗公式，其反演精度為18cm［3]。假設表面相關時間是有效波高的函數，并定義有效相關時間為［3]

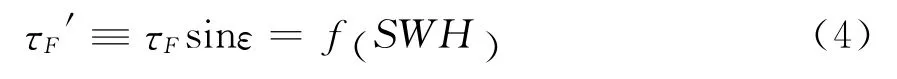
為了更準確的適應深海數據，引入SWH偏移參數SWH0和尺度參數γ，最終得到有效波高與有效相關時間的模型［3]（SWH＞SWH0時有效）：

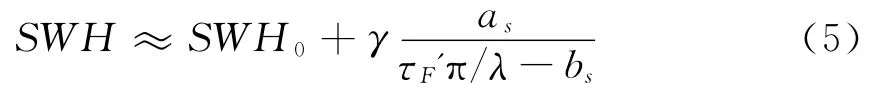
在風區不夠長而且海床低的海域時，海浪不能充分成長，用海浪譜推導有效波高與相關時間之間的理論關系就很困難［5]。邵連軍等人在論文［5]中提出了數據擬合的一個經驗模型，該模型中同樣使用了有效相關時間的概念［5]，模型表達式為

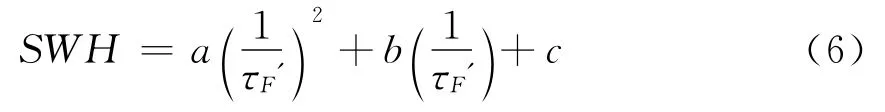
兩個模型中的參數須根據具體測量區域情況和接收平臺高度確定，為探索更為準確的測量方法利用所采集的數據對以上兩個模型進行了分析比對。

1.4 誤差分析

GPS衛星高度遠遠大于接收機高度，可以認為直射信號和反射信號經歷同樣的傳播路徑，但是反射波有一個附加路徑，除此之外兩種信號受到的電離層和中性大氣折射的影響相等，這個反應在指數項上，通過干涉處理方法，可以基本達到消除共同傳播路徑的大氣影響的目的［3，5]。反射波的附加路徑上，接近海面的高度范圍內，對流層折射指數較大，因此，它對信號的影響不應忽略。

2 實驗結果分析

采用如圖1所示的有效波高反演系統，采用的接收機輸出為直射和反射信號的相關值復數序列，從輸出中分別提取直射和反射信號幅度最大的相關值，得到干涉復數場ICF，求得干涉復數場的自相關函數，通過擬合得到連續的干涉復數場擬合函數并得到ICF的相干時間，求出有效相關時間，利用半經驗模型計算獲得有效波高值。整體過程如圖1所示。

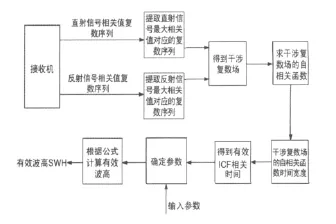
圖1 利用干涉復數場有效波高反演系統

測定有效波高采用兩個半經驗模型，分別為F.Soulat等人在文獻［3]中提出的半經驗模型和邵連軍等人在文獻［5]中提到的半經驗模型。為敘述方便，將其分別設為模型1，模型2。模型1中，有效波高SWH和有效ICF自相關時間寬度的關系模型如下［3]：

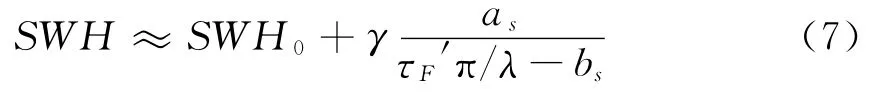
式中：as和bs分別為適應實際測量地點的參數；SWH 為有效波高；λ為信號波長；τF′為ICF自相關函數有效時間寬度。引入SWH 偏移參數SWH0和尺度參數γ.

因為不同的海域所適用的模型參數有差別，通過采集的數據確定了適用于本次實驗地點的模型參數：

SWH0＝ －0.01，

as＝3.50878，

bs＝0.0842，

γ＝1.8.

模型2中，同樣使用了有效相關時間的概念，模型表達式為［5]

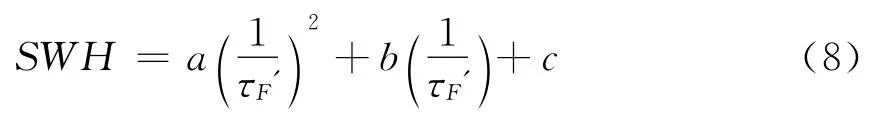
為了適應本論文采用數據的實際地點情況和接收平臺高度情況，采用所采集數據確定模型參數：a＝0.08，b＝－0.073，c＝0.5767。下面將對這兩個模型進行驗證。

在MATLAB環境下進行分析，創建圖形用戶界面如圖2所示。

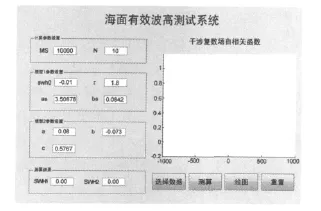
圖2 海面有效波高測試系統用戶界面

采用的數據為北航和氣象局相關人員于2009年11月在博賀海洋氣象科學實驗基地采集的數據。采集數據的設備包括DDMR接收機，天線2個，電腦2臺。對比數據采用WaMos海浪測波儀測定的有效波高，基礎誤差為0.5m.下面以13號衛星某時段的觀測數據為例分析實驗結果，該數據是10s的觀測值，相關值為5組多普勒頻移，每組55個碼延遲。從13號衛星0多普勒頻移組直射信號中選取1ms相關值，如圖3所示；13號衛星直射信號和反射信號相關值幅度最大值波形分別如圖4，圖5所示；對應的干涉復數場波形如圖6所示；干涉復數場自相關函數波形以及其擬合波形如圖7所示。

在數據處理長度為10s，相干積分次數為10的情況下，得到ICF自相關函數如圖7所示。

采用模型測算結果與對比數據比對結果如表1所示。

采集數據期間的有效波高與測波儀所測波高的最大偏差：

采用模型測算波高結果與對比數據對比圖如圖8所示。

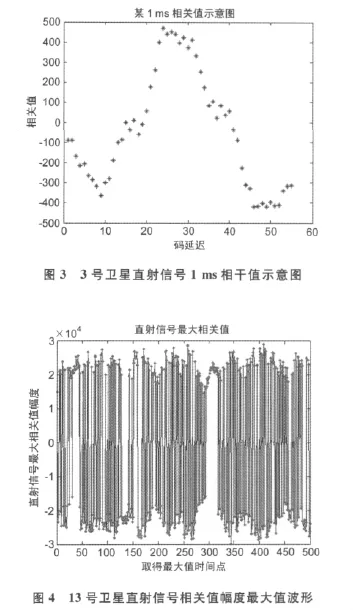
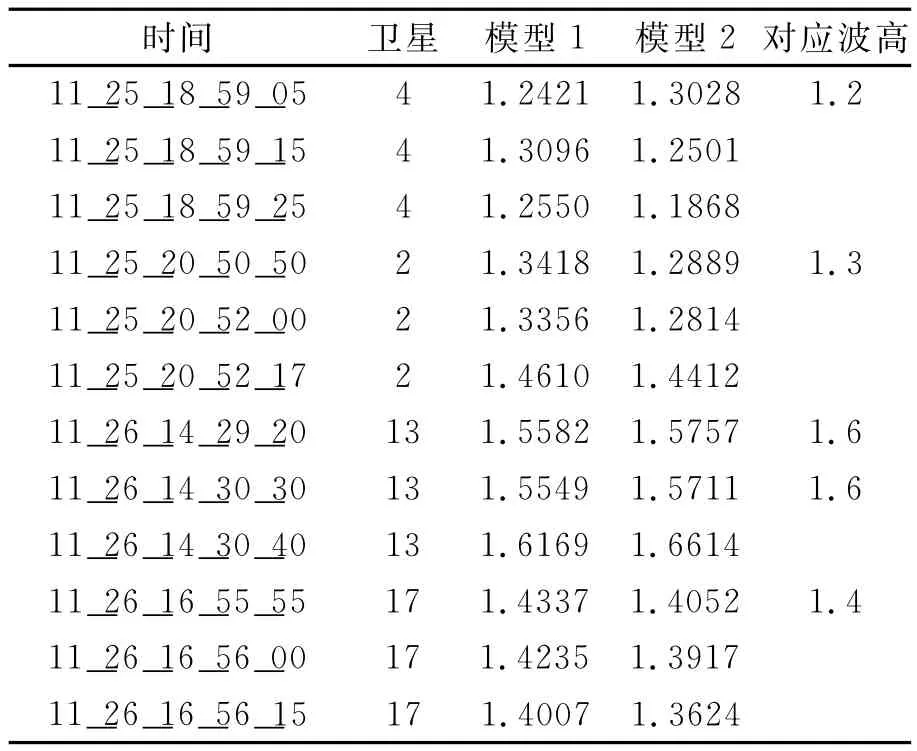
表1 測量結果與實測結果對比表

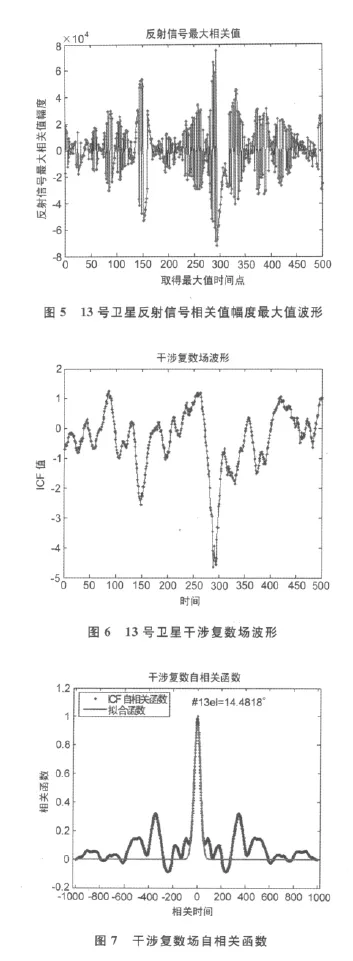
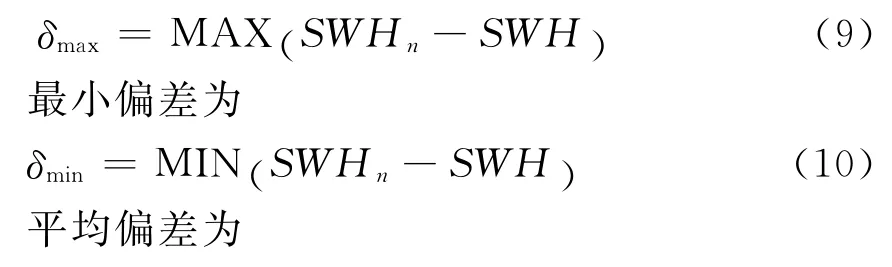
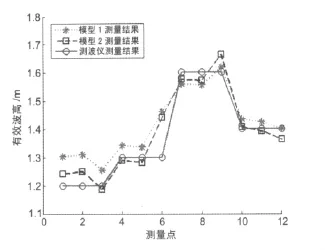
圖8 有效波高測量結果對比圖

式中：SWHn是本文模型測得的有效波高值，其中（n ＝ 1，2）；SWH 是利用測波儀測量的有效波高值；δi是每次計算的SWHn和SWH 之間差值，反映二者偏差大小；δmax和δmin是SWHn和SWH 之間最大和最小差值；δmean是SWHn和SWH 之間偏差的平均值，反映二者偏差的平均程度；D（δ）是δ的方差，反映δ的平穩程度。

使用示例數據的分析結果如表2所示。

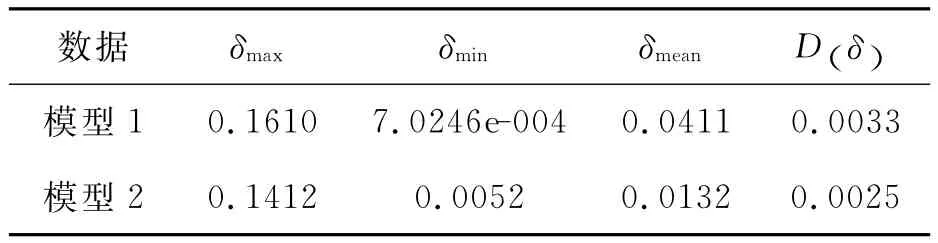
表2 有效波高測量分析數據表

由上述對比可以看出，本系統所測得的有效波高與測波儀測得的波高比較一致，模型2的平穩度和偏差的平均程度要好于模型1。

3 結 論

通過具體的分析和實現，本文基本達到了最初設定的低成本并簡單有效地計算海洋有效波高的目標。應注意的是，數據處理參數可能對結果有所影響，在一段時間內有效波高可能變化較大，如果數據處理長度Ms過長，時間精確度將不能夠達到要求造成有效波高測量不準確；但數據處理長度過短，有效波高沒有變化，這樣就浪費了計算時間和存儲資源。因此，需要采用合適的數據處理長度。這種方法最大的優勢是成本低，當然，此系統還存在一些缺點和不足，如采用的ICF和SWH之間的模型不夠精準，并且是否可用于所有海域，還有待于進一步研究。

因本實驗需要大量數據驗證分析，但是由于現實條件有限未能得到足夠的實驗數據。需要說明的是，本實驗采用的對比數據測得波高的時間分辨率不高，對結果分析時，認為對比數據短時間內的波高值相同，另外所采用的測波儀基礎誤差較大對結果的精度及參數確定產生了較大影響，有待于改善。

［1]張益強.基于GNSS反射信號的海洋微波遙感技術［D].北京：北京航空航天大學，2008.

［2]Hajj G A，Zuffada C.Theoretical description of a bistatic system for ocean altimetry using the GPS signals［J].Radio Science，2003，38（5）：1089－1107.

［3]Soulat F，Caparrini M，Germain O，et al.Sea state monitoring using coastal GNSS－R ［J].Geophysical Research Letters，2004，31（21）：303－307.

［4]Ruffini G，Soulat F.On the GNSS－R interferometric complex field coherence time ［EB／OL].（2004－06－21）.http：／／arXiv.org／abs／physics／0406084v2.

［5]邵連軍，張訓械，王 鑫 ，等.利用GNSS－R信號反演海浪波高 ［J].武漢：武漢大學學報·信息科學版，2008，33（5）：1671－8860.