鐵路編組站布局的雙層規劃方法研究

殷 勇，彭其淵

(西南交通大學 交通運輸與物流學院，四川 成都 610031)

鐵路特編點組和站自的然合集理散布規局律是，指正在確鐵地路選網擇上編按組車站流的位置，經濟合理地確定其規模[1]。由于路網上編組站之間的分工相互關聯，即每一處編組站的建設(新建或改擴建)，都會對路網上車流改編方式產生影響，因此編組站布局不能就點論點，而應該從路網整體優化的角度加以考慮。長期以來，由于缺乏有效的優化方法，現有的編組站布局決策基本上立足于經驗判斷。通過分析當前我國鐵路編組站布局存在的主要問題，結合我國鐵路車流的特點和變化，對未來編組站的合理布局及其發展方向進行了探討[2-3]。近幾年，隨著車流組織研究的進一步深入，國內部分學者運用現代優化方法對編組站布局問題進行了研究，如嘗試建立編組站布局規劃優化模型[4]，研究技術站布局的雙層規劃優化方法[5]。因此，探討運用雙層規劃方法提出編組站布局問題，建立編組站布局雙層規劃模型及求解算法，具有積極的意義。

1 編組站布局問題的描述

隨車流量的增長及車流結構的變化，需要對路網編組站的位置和規模進行必要的調整，以適應車流不斷變化的需求。一般而言，編組站布局問題可以描述為，在有限資金投入的條件下，選擇最優投資策略，通過改進現有編組站的布局，包括新建編組站、擴大或減小現有編組站規模等，使路網中車流組織達到最優。編組站布局問題可以從建設投資費用和車流組織費用兩個方面考慮。

編組站的建設投資費用主要取決于新建或改擴建編組站的建設規模；路網車流組織費用是對于給定的編組站布局方案，車流組織實現的最優費用。一方面，投資者通過投入大量資金，采用新建或改擴建等措施對既有編組站布局進行調整，以滿足車流不斷增長及其組織優化的需求；另一方面，運營部門通過調節路網上的車流組織方式，以適應給定的編組站布局狀況。

編組站布局問題可用雙層規劃加以描述：上層規劃表示決策者為了達到車流組織最優的目的而采取的最優投資策略，下層規劃代表給定編組站布局方案條件下的車流組織優化。同時假設：對于任意給定的上層決策變量 (編組站布局方案)，都可以從下層規劃中求得一個惟一的最優車流組織方案。上層決策通過設置不同的編組站布局方案影響下層決策，因而限制了下層決策的可行約束集，而下層決策行為又會通過車流組織方案對應的費用影響上層的目標函數。

2 編組站布局的雙層規劃模型

2.1 上層規劃模型

對于一個給定的路網 (V，E)，這里 V 是所有備選編組站的集合，E 為路網上的邊集。設 k 是路網上的某個備選編組站，引入 0-1 變量 xk，定義為：

首先，編組站的選擇是有條件的，主要考慮在路網的交匯處而且有大量車流集散。因此，處于路網主要干線的交匯處而且有大量到發車流的節點構成備選編組站集合V，同時為減少可能的組合方案數量，可結合專家經驗將 V 分為兩類，即 V＝{V1，V2}。其中，V1表示必選編組站集合，相應的約束為：

V2表示可能設為編組站的集合，相應的約束為：

對于被選設的編組站，還需進一步確定其新建或改擴建方案。設 k 站被選設為編組站，相應的新建或改擴建方案有 P (k) 個 (包括維持既有編組站規模)，引入第2組 0-1 變量 xkp，定義為：

在路網上某個特定地點，若新建或改建既有編組站，可選擇的方案很有限。我國鐵路主要推薦的站型是：單向一級三場、二級四場、三級三場和雙向三級六場，其他站型都是在此基礎上派生出來的，因此 P(k) 是有限的。就 k 站而言，雖然有 P (k)個方案，但是在規劃期內這些方案是互不相容的，且當 xk＝1 時，必有一個方案被選擇，因此可以用方案互不相容約束來表達。

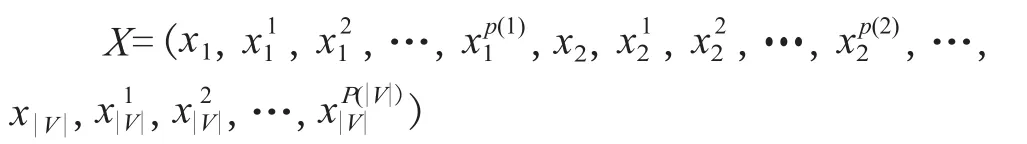
以編組站建設投資費用和路網上車流組織費用之和最小為目標函數，建立上層規劃模型為：

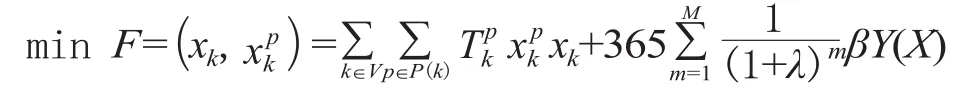
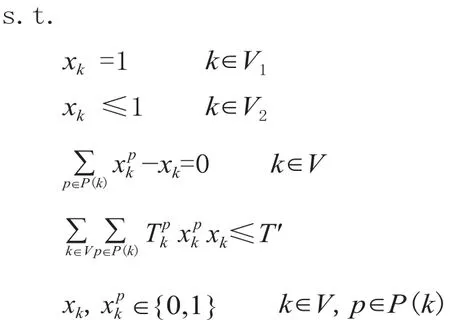
式中：M 為規劃年數；λ 為貼現率；β 為車小時的單價；Y (X ) 表示路網上的車流組織費用，其值為決策變量 X 的函數，不同的編組站布局方案，對應不同的車流組織費用。

2.2 下層規劃模型

下層規劃是針對不同的編組站布局方案，求相應路網上的車流組織優化問題，即列車編組計劃(簡稱TFP) 問題。關于 TFP 的研究，特別是技術站單組列車的編組計劃，很多學者和專家都已進行了長時間的系統研究和探索，得出了一些重要結論，建立了較為完善的規劃模型。其中比較著名的有混合整數規劃模型、線性 0-1 規劃模型、二次 0-1 規劃模型、網絡優化模型、有利去向模型、階躍函數模型及高次 0-1 規劃模型等[6-8]。

研究車流組織優化問題，考慮其編組站布局規劃方案是變化的，但對于給定的一組編組站布局方案，則與原 TFP 問題完全一致，借鑒TFP 的網絡優化方法構建下層規劃模型 (這里約定車流組織以給定的車流徑路為前提)。

對于某一編組站選址和規模方案 X，其中編組站集 SX＝{s(1)，s(2)，…，s(n)}，全體可能的編組去向集 AX＝{a(i,j)：s(i),s( j)∈SX}，必開編組去向集，禁開編組去向集，改編能力UX＝{u(i)：s(i)∈SX}、編組去向車流下限VX＝{v(i,j)：a(i,j)∈AX}、編組去向數上限WX＝{w(i)：s(i)∈SX}、集結車小時CX＝{c(i,j):a(i,j)∈AX}、改編車小時消耗TX＝{t(i)：s(i)∈SX}、車流量FX＝{f (i,j)：s(i)，s ( j)∈SX}，車流徑路LX＝{L(x,y)：x,y＝1,2,…, n}，編組去向集為Bx，則建立模型：

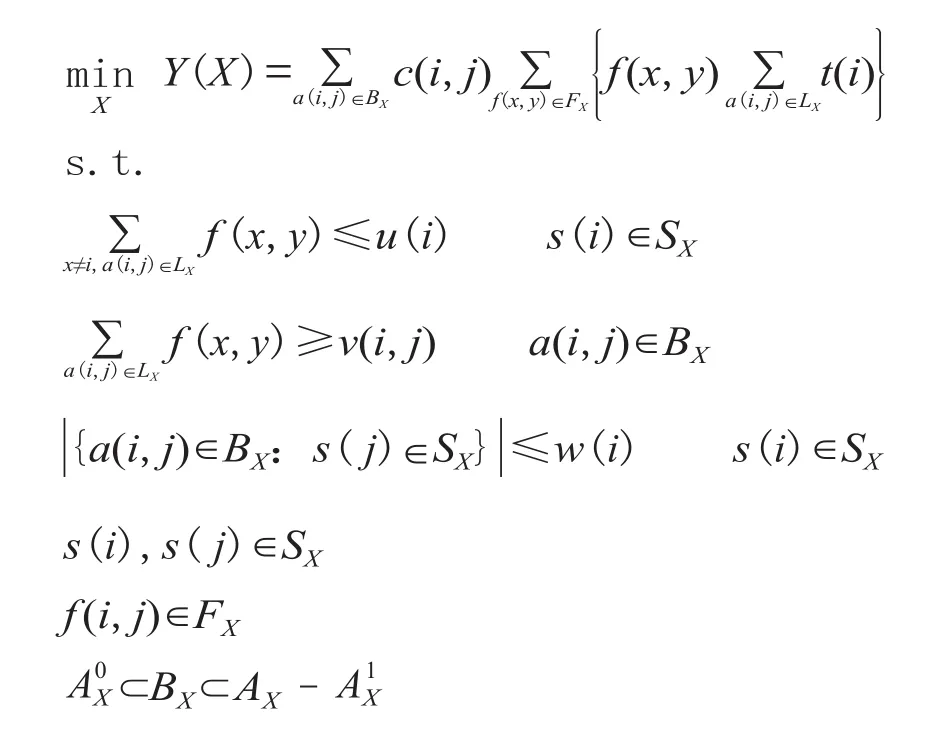
3 模型的算法研究

一般雙層規劃問題的求解都是非常復雜的，即使是很簡單的雙層線性規劃問題也是NP-hard問題，不存在多項式求解算法[9]。求解雙層規劃問題的關鍵是找到反應函數的具體形式，對于連續變量情況，可以通過靈敏度分析方法得出變量之間的導數關系，繼而可以利用泰勒展開式對反應函數進行近似求解[10]。本文建立的雙層規劃模型上層是一個離散變量的非線性優化，下層是一個大規模的組合優化，此時的雙層規劃問題更加復雜，用傳統的數值算法很難求解。

遺傳算法 (GA) 提供了一種求解復雜系統優化問題的通用框架，以其具有的并行搜索能力、自適應性和可直接應用等優點，適合于求解大規模任意目標函數的全局優化問題。但簡單的遺傳算法在許多情況下不是十分有效，容易產生早熟現象及局部尋優能力較差等問題，而將遺傳算法與問題的特有知識集成到一起，或者在遺傳算法中融合其他算法的思想和方法，構成一種混合遺傳算法，則求解性能有可能達到極佳[11]。一般有兩種混合策略：①把遺傳算法和原有算法有效結合，設計一個新的混合算法；②采用原有算法的編碼或把原有算法中的一系列變換結合到混合遺傳算法中。混合GA 最常見的形式是在 GA 典型的重組選擇循環中嵌入一塊附加的局部優化模塊。結合本文的模型特點，將遺傳算法與求解車流組織優化問題相結合，從而構造出適合求解編組站布局雙層規劃模型的混合遺傳算法。

關于 Y (X ) 的計算，有關研究通過分析模型的不同特點，提出了多種有針對性的算法，除傳統的以手工操作為主的絕對計算法和表格分析法以外，還成功地運用單純形算法、分枝定界算法、拉格朗日松弛算法等進行計算機求解，并且發展了諸如有序組合樹算法、網絡拓撲變換法、二次0-1 規劃法等。值得指出的是，20 世紀 80 年代以來，國內外學者運用現代新興的智能優化方法，如遺傳算法、模擬退火、禁忌搜索及人工神經網絡等方法解決車流組織優化問題，在實現大規模、多約束、非線性車流組織優化方面表現了良好的性能。編組站布局雙層規劃模型的混合遺傳算法框架如圖1所示。按照模型的詳細計算過程[12]，根據計算結果并結合其他的編組站布局影響因素，提出我國鐵路編組站布局的調整方案。

4 結束語

編組站的合理布局與分工，對提高鐵路運輸生產效率和水平、確保路網的安全暢通、加速機車車輛周轉、縮短貨物送達時間、提高經濟效益和社會效益、促進鐵路運輸業協調可持續發展十分重要。通過分析建立模型，將求解車流組織費用的計算模塊與 GA 結合，構建了求解編組站布局雙層規劃模型的混合遺傳算法，適用于實際路網中的編組站布局問題決策。研究結果表明，應用雙層規劃方法解決編組站布局問題是合適的，建立的編組站布局雙層規劃模型能夠貼切地描述編組站布局方案和車流組織優化的關聯關系。

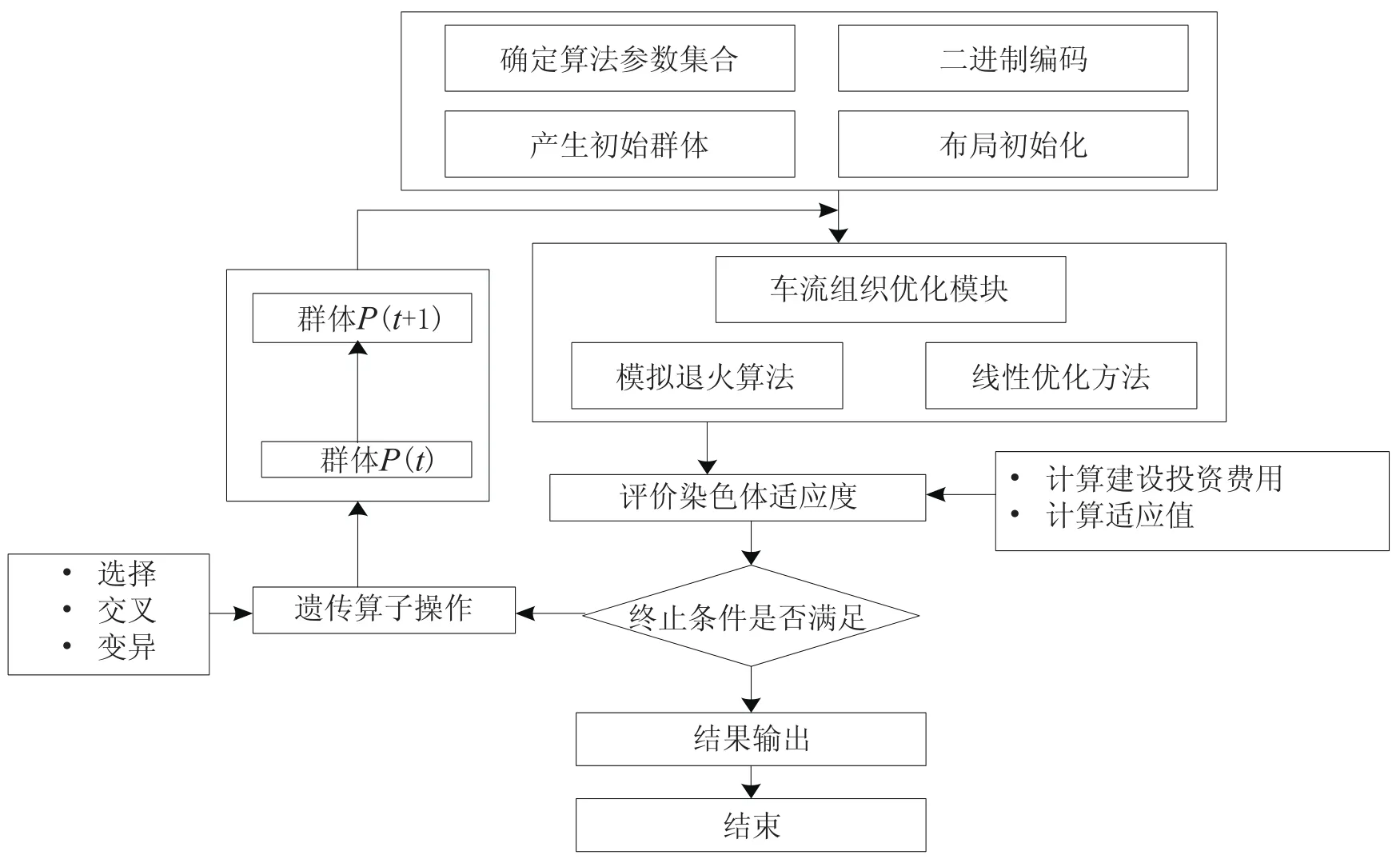
圖1 求解模型的混合遺傳算法框架

[1]劉其斌，馬桂貞. 鐵路站場及樞紐[M]. 北京：中國鐵道出版社，1999.

[2]吳家豪. 中國鐵路跨越式發展新時期的編組站分類與布局探討[J]. 鐵道經濟研究，2005(4)：33-38.

[3]趙海寬. 基于運力資源優化配置和運輸組織創新的鐵路編組站合理布局[J]. 鐵道運輸與經濟，2009，31(12)：4-7.

[4]林柏梁，徐忠義, 黃 民，等. 編組站布局規劃模型[J]. 鐵道學報，2002，24(3)：5-8.

[5]史 峰，方琪根，黎新華，等. 技術站布局的雙層規劃優化方法[J]. 鐵道學報，2003，25(2)：74-79.

[6]胡思繼. 鐵路行車組織[M]. 北京：中國鐵道出版社，1998.

[7]林柏梁，朱松年. 路網上車流徑路與列車編組計劃的整體優化[J]. 鐵道學報，1996，18(1)：1-7.

[8] 史 峰，孔慶鈐，胡安洲. 車流徑路與編組計劃綜合優化的網絡方法[J]. 鐵道學報，1997，19(1)：1-6.

[9] 劉樹安，尹 新，鄭秉霖，等. 二層線性規劃問題的遺傳算法求解[J]. 系統工程學報，1999，14(3)：280-285.

[10] 高自友，宋一凡，四兵鋒. 城市交通連續平衡網絡設計一理論與方法[M]. 北京：中國鐵道出版社，2000.

[11] S·Voget. Theoretical analysis of genetic algorithms with infinite population size[J]. Complex Systems，1996(10)：167-183.

[12] 殷 勇. 鐵路編組站布局規劃方法與調整對策研究[D]. 成都：西南交通大學，2008.