LS模型下信用價差看跌期權定價研究

張海永，李慶宏

(滁州學院數學科學學院，安徽 滁州 239000)

0 引言

1973年，Fischer Black與Myron Scholes在《政治經濟學雜志》發表研究論文"The Pricing of Options and Corporate Liabilities"，提出了著名的Black－Scholes期權定價公式，此公式假定在期權有效期內，無風險利率、股票資產期望收益變量和價格波動率是恒定的。此后，無數的研究學者就該模型存在的問題和多條假設進行改進，希望使得定價更加精確或者減少一些假設。

1995年，Longstaff和Schwartz提出無風險利率rt和信用價差st都滿足Vasicek模型，

其中αr和αs是正常數，分別表示利率和價差的均值回復速度;γr和γs為正常數，分別表示利率和價差的長期平均水平;σr和σs為常數，分別是它們的波動率。是標準布朗運動ρ為常相關系數。模型⑴、⑵ 被稱為Longstaff－Schwartz模型，簡稱LS模型。

本文主要研究在LS模型下怎樣為幾何平均浮動執行價的亞式信用價差看跌期權定價。

1 幾何平均浮動執行價的亞式信用價差看跌期權定價

先給出一個有用的引理。

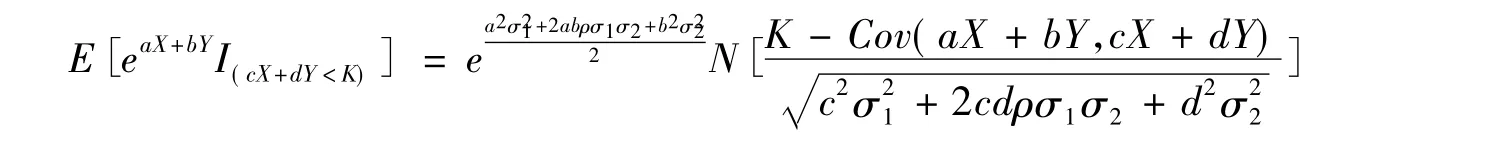
其中 a、b、c、d 是實數且 c、d 不同時為零。

定理 在LS模型下，到期日為T幾何平均浮動執行價的亞式信用價差看跌期權價值為

證明:到期日為T的幾何平均浮動執行價亞式信用價差看跌期權價值可以表示為:

2 結語

Black－Scholes期權定價公式對無風險利率的假設條件較為嚴格，本文放寬了這個假設條件。在無風險利率和標的信用價差均服從Vasicek模型(即Longstaff＆Schwartz模型)的條件下，從測度及標準布朗運動的角度出發，推導出了LS模型下幾何平均浮動執行價的亞式信用價差看跌期權定價公式，在使用時，這個定價公式比Black－Scholes期權定價公式更能適應金融市場的實際情況。……