基于動態規劃算法的故障恢復重構

張 浩 和敬涵 薄志謙 胡 偉 李 珂 周 文

（1.北京交通大學電氣工程學院 北京 100044 2.阿爾斯通電網自動化公司 斯塔福德郡 ST17 4LX 英國 3.河北省電力研究院 石家莊 050021）

1 引言

隨著電網結構、運行方式的日趨復雜和用戶對供電可靠性要求的不斷提高，電網的自愈恢復與重構作為智能電網的一項重要功能已經成為電力系統需要迫切考慮的問題之一[1-3]。配電網的故障恢復重構作為網絡重構的一種，是指在故障定位和隔離的基礎上，在不發生系統安全越限的條件下，通過網絡重構快速恢復對非故障區失電負荷的供電。該過程一般要在綜合考慮開關操作次數、饋線裕度、負荷恢復量、網絡約束、用戶優先級等因素下，提出優選的供電恢復方案[4]。這類問題一般不可微、不連續、多維、多約束條件、高度非線性化。對于此類問題的優化求解一直是國內外的研究熱點。目前相關的求解思路主要有邏輯法[5]、專家系統[6]、啟發式搜索[7-9]，以及多種方法的混合[10-11]。

動態規劃（dynamic programming）是運籌學的一個分支，它是解決多階段決策過程最優化問題的一種方法[12]。本文在總結現有算法成果的基礎上，將故障恢復重構過程轉化為一個多階段決策過程，并設計了以動態規劃算法為核心的故障恢復重構方案。該方案主要考慮配電網中功率不足時的負荷恢復問題，通過對待恢復區的劃分降低了算法的復雜度，提高了算法的運行效率。

2 問題描述

故障恢復過程中，要盡可能多地恢復非故障失電的負荷，還要使開關操作次數最少。同時，為了在盡可能短的時間內恢復對停電區域的供電，減少用戶的不滿意程度，提高供電可靠性，恢復策略要具備較高的實時性。

重構的約束條件包含等式約束和一系列不等式約束。等式約束主要是潮流約束；不等式約束包括：饋線容量的約束、線路電流的約束、母線電壓的約束、變壓器過載約束[13]等。

為方便描述和簡化計算，故障恢復重構進行如下假設：

（1）配電網中的故障元件均已隔離，且非故障帶電區運行正常。

（2）已進行網絡的簡化等效，所有支路均有開關且可操作。

（3）重構前后網損近似相等，且各支路網損已包含在各節點功率參數內。

以圖1所示的33節點系統為例，該系統結構在文獻[14]的基礎上添加了2個電源（S1，S2）。

圖1 33節點網絡結構示意圖Fig.1 Diagram of 33-bus network

圖中細實線為正常運行時的計算支路（如支路2-3），虛線為常開的聯絡支路（如支路8-21）。若節點7發生故障并被切除，則發電機S2退出運行，與節點7相連的下游區域（8～18節點）為非故障失電區（待恢復區）。

3 恢復重構算法

3.1 恢復區分割

非故障失電區可能同時連接有多個聯絡開關可用于負荷轉供（如圖1中的8-21；12-22；18-33）。這就需要考慮將其中的負荷節點分割為多個區域分別進行負荷恢復（簡稱為分區）。

分區需要綜合考慮聯絡支路容量、聯絡開關和網絡結構等要求，最多分割為與聯絡支路等數量的負荷區（待恢復區內部的聯絡支路不考慮，如圖1中支路9-15），且每個負荷區的容量與該聯絡線的傳輸容量相匹配，盡量使多個負荷區的負荷量平衡，并能滿足各約束條件。

分區時首先將恢復區內的所有開關閉合，再采用深度優先搜索方法，找到不同聯絡開關間的連通路徑，并在該路徑上斷開一個開關，以此類推來實現整個分區過程。

設Lm(y)為分區數量為m的最優分區方案，則對于任一方案y，其負荷均衡系數計算方法為

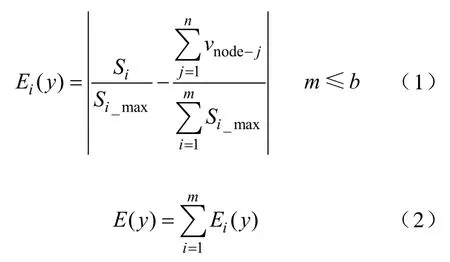
式中，Ei(y)為方案y中聯絡支路i的均衡系數；E(y)為方案y的均衡系數；Si和Si_max分別為聯絡支路i上所分配的負荷容量和該支路所能承受的最大容量；vnode-j為節點j的負荷容量；n為需要恢復的節點數；b為可用于負荷轉供的聯絡支路數。

開關操作比重系數為

式中，k為開關操作次數；α為開關系數，系數越高，開關操作數對分區結果的影響越重。

從而，Lm(y)計算方法為

一般來說，為了覆蓋更多的可能分區策略，分區數m應取[1，b]間的所有自然數。每種分區方案均可獨立進行重構計算，互不干擾，這就給實際運行提供了較為寬裕的選擇余地。在實時性要求較高的情況下也可僅選擇m=b以加快求解速度，當然這樣會增加獲得非最優解的可能性。實際運行中，可根據重構需求對α和m進行不同的取值來選擇合適的分區方案。例如，對于圖1所示網絡結構，取m=b=3，α=2時的分區方案為：[8，9，10]，[11，12，13，14]，[15，16，17，18]。

3.2 動態規劃模型

動態規劃所研究的多階段決策問題是指這樣一類決策過程[12]：它可以分為若干個互相聯系的階段，在每一階段分別對應著一組可以選取的決策，當每個階段的決策選定以后，過程也就隨之確定。把各個階段的決策綜合起來，構成一個決策序列，稱為一個策略。顯然由于各個階段選取的決策不同，對應整個過程就可以有一系列不同的策略。

動態規劃本身是一種方法而不是一種算法。本文結合配電網的恢復重構需求，對動態規劃中的相關概念進行解釋和設計以形成用于故障恢復的動態規劃重構算法。

（1）階段。階段是對整個過程的自然劃分。將聯絡支路作為計算階段，則其也可以用聯絡支路符號i表示。用ci表示第i階段進行轉供的負荷節點串，用Ci表示第i階段的節點串集合。

（2）狀態。每個階段開始時所處的自然狀況叫做狀態。定義網絡的功率裕量與節點串的組合為狀態。用hi表示第i階段的功率裕量，xi表示該階段的一個狀態變量，Xi表示允許狀態集合。則有

（3）決策。當一個階段的狀態確定后，可以做出各種選擇從而演變到下一階段的某個狀態，這種選擇手段稱為決策。用ui(xi)表示第i階段處于狀態xi時的決策變量，Ui(xi)表示xi的允許決策集合。

（4）策略。決策組成的序列稱為策略。由初始狀態x1開始的全過程的策略記作p1m(x1)，即

式中，m為計算階段數（分區數）。

（5）狀態轉移方程。在確定性過程中，一旦某階段的狀態和決策為已知，下階段的狀態便完全確定。用狀態轉移方程表示這種演變規律，寫作

（6）指標函數和最優值函數。指標函數是衡量過程優劣的數量指標，用fi,m(Xi，ui，Xi+1，…，um)表示，i=1，2，…，m-1。指標函數的最優值，稱為最優函數，記為fi(Xi)，表示從第i階段的狀態Xi開始到第m階段的終止狀態的過程，采取最優策略所得到的指標函數值，即

式中，opt表示最優結果。

3.3 恢復重構的動態規劃算法

網絡的功率裕量表示該網絡可用于轉供的最大負荷量。故障被隔離后，網絡的初始裕量為

式中，h1為重構計算的初始功率裕量；S為網絡中的電源提供的總功率；vuse為網絡中未失電的負荷總量；β為可靠系數，優選取值0.8～0.95。

每一階段中，根據所選節點的先后順序不同而形成不同的操作序列，該序列可用節點串表示。例如3.1節舉例分區方案中的一個分區[11，12，13，14]，從節點12開始，恢復供電的操作序列有三個（見圖2）：

序列1｛(12)；(12,13)；(12,13,14)；(11,12,13,14)｝；

序列2｛(12)；(12,13)；(11,12,13)；(11,12,13,14)｝；

序列3｛(12)；(11,12)；(11,12,13)；(11,12,13,14)｝。

圖2 節點串序列拓展示意圖Fig.2 Node string sequence diagram

由此，對負荷節點恢復順序的選擇轉化為對操作序列中節點串的選擇。

不同階段的操作序列進行組合，生成計算序列組。用ni表示第i階段的操作序列數，則計算序列組數有

對于每組計算序列的第i階段任一xi，有

式中，vci-1表示選節點串ci-1的容量。

從而第i階段有效節點串集合為

式中，R表示重構過程中各類電氣約束條件。

有效節點串的提取可減少計算組合數，從而提高計算效率，加快算法的實現。

定義f（ixi）表示狀態變量xi的允許決策集合與前一階段每個狀態變量的最優結果進行組合的最優結果，有

對于第i階段，計算出每個狀態變量的fi函數以后，記下hi及所選的節點串ci-1。繼續計算該階段的最優函數，記為f（xi）。

定義C0=φ，則對于第1階段的任一狀態變量x1，可得到該狀態的fi函數為

利用上述方法可以得到第1階段的最優函數f1(x1)及f1(X1)。進而求取各階段最優目標f(Xi)達到本網絡容納負荷量最優。

算法實施描述如下：

（1）根據重構請求，啟動重構算法。獲取故障發生前的網絡相關信息（如網絡的潮流、電壓、功率分布等），計算待恢復區負荷容量及網絡功率裕量。

（2）進行分區計算，并計算序列組的生成。同時判斷網絡功率裕量和網絡結構是否足夠恢復所有負荷。是，則直接輸出計算結果；否，則轉（3）。

（3）判斷是否已經完成所選序列組的計算。若是，則輸出計算結果；否，則進行序列選擇并轉（4）。

（4）計算第i階段中網絡的功率裕量hi及該階段的有效節點串集合optCi。計算最優函數fi(xi)及fi(Xi)。判斷是否已經遍歷聯絡支路及待恢復區的所有節點。若是，則轉（5）輸出計算結果；若否，則轉（4）進行循環計算。

（5）輸出計算結果。

重構算法流程如圖3所示。

圖3 算法流程圖Fig.3 Flow chart of the algorithm

4 算例分析

用33節點和69節點兩個算例來驗證本文算法的有效性。采用簡單遺傳算法（SGA）和本文所用動態規劃算法（DP）進行計算結果對比。遺傳算法初始種群40個，迭代次數為50，交叉變異概率分別為0.8和0.07。動態規劃算法分區數m取[1，b]間的所有自然數。為簡化描述，這里僅以有功功率為例進行功率計算，所有節點優先級相同，假設所有支路上限容量均為5MW，網絡初始功率裕量h1=0.5MW。兩種算法均采用重復計算100次求平均的方法計算耗時。

驗證平臺電腦CPU為奔騰四2.6GHz，內存1GB，操作系統為Windows XP，程序采用Matlab編寫。

4.1 33節點算例

如圖1所示33節點系統，節點功率數據來自文獻[14]，并在其基礎上添加了兩個電源。所有負荷節點總有功容量：3.715MW。假設節點7出現故障并被切除，則電源S2停運，非故障失電區容量為0.765MW。有三個分區方案，分別為

兩種算法均能恢復0.495MW的負荷，且均找到兩種最優結果（最大恢復容量和開關操作數均相同且最優）。由于篇幅所限，這里僅列出一種最優結果見表1。

表1 33節點恢復重構計算結果Tab.1 Results with 33-bus system

忽略兩者在具體編程過程中的編程風格不一致等情況帶來的影響。簡單遺傳算法由于在交叉運算中易產生大量不可行解，耗時較長，而且在部分重復計算過程中收斂于非最優解；而動態規劃算法每次計算結果均相同，耗時較短。最終恢復供電結構如圖4所示，經潮流計算證明該結果可行。

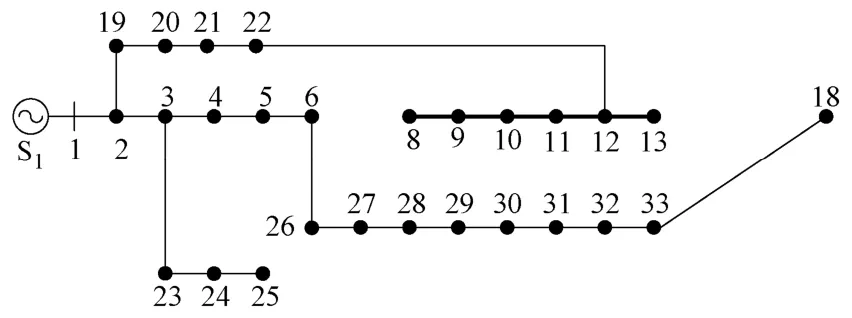
圖4 33節點恢復后結構Fig.4 33-bus network reconfiguration

4.2 69節點算例

圖5 69節點網絡結構示意圖Fig.5 Diagram of 69-bus network

圖5 所示為69節點網絡結構系統，節點功率數據來自文獻[15]，并在其基礎上添加了兩個電源。假設節點10出現故障并被切除，則電源S2停運，非故障失電區容量為0.7398MW。三個分區方案為

計算結果與前一算例類似，兩種算法僅在計算時間上有明顯差別。動態規劃算法比簡單遺傳算法具有更短的計算周期。表2為16個最優結果中的一個。

表2 69節點恢復重構計算結果Tab.2 Results with 69-bus system

5 結論

本文結合配電網重構問題的特點和動態規劃思想提出一種電網恢復重構方案。通過對非故障失電區的分區、計算序列生成，將配電網恢復重構過程轉換為一個多階段決策過程，并以此構建了多階段決策模型，設計了動態規劃算法，可在網絡功率裕量不足時快速實現網絡重構，從而提高系統的供電可靠性，減少負荷斷電時間。

[1] 余貽鑫,欒文鵬.智能電網述評[J].中國電機工程學報,2009,29(34): 1-8.Yu Yixin,Luan Wenpeng.Smart grid and its implementations[J].Proceedings of the CSEE,2009,29(34): 1-8.

[2] Heydt G T.The next generation of power distribution systems[J].IEEE Transactions on Smart Grid,2010,1(3): 225-235.

[3] 王明俊.自愈電網與分布能源[J].電網技術,2007,31(06): 1-7.Wang Mingjun.Self healing grid and distributed energy resource[J].Power System Technology,2007,31(06)1-7.

[4] 陳竟成,徐德超,于爾鏗,等.配電網故障恢復系統[J].電力系統自動化,2000,24(4): 46-51.Chen Jingcheng,Xu Dechao,Yu Erkeng,et al.Distribution fault detection,isolation and restoration system in a distribution management system [J].Automation of Electric Power Systems,2000,24(4):46-51.

[5] 劉健,倪建立,鄧永輝.配電自動化系統[M].北京:中國水利水電出版社,1999.

[6] Men Shen T.Development of an object-oriented service restoration expert system with load variations[J].IEEE Transactions on Power Systems,2008,23(1): 219-225.

[7] Sudhakar T D,Vadivoo N S,Slochanal M R.Heuristic based strategy for the restoration problem in electric power distribution systems[C].2004 International Conference on Power System Technology,Singapore,2004,1: 635-639.

[8] Luan W P,Irving M R,Daniel J S.Genetic algorithm for supply restoration and optimal load shedding in power system distribution networks[J].IEE Proceedings Generation,Transmission and Distribution,2002,149(2): 145-151.

[9] Watanabe I,Nodu M.A genetic algorithm for optimizing switching sequence of service restoration in distribution systems[C].Congress on Evolutionary Computation,CEC2004,Portland,Oregon,America,2004,2: 1683-1690.

[10] Hsiao Y T,Chien C Y.Enhancement of restoration service in distribution systems using a combination fuzzy-GA method[J].IEEE Transactions on Power Systems,2000,15(4): 1394-1400.

[11] Seong Il L,Seung Jae L,Myeon Song C,et al.Service restoration methodology for multiple fault case in distribution systems[J].IEEE Transactions on Power Systems,2006,21(4): 1638-1644.

[12] 吳祈宗.運籌學[M].北京: 機械工業出版社,2007.

[13] 徐青山.電力系統故障診斷及故障恢復[M].北京:中國電力出版社,2007.

[14] Baran M E,Wu F F.Network reconfiguration in distribution systems for loss reduction and load balancing[J].IEEE Power Engineering Review,1989,9(4): 101-102.

[15] Baran M E,Wu F F.Optimal capacitor placement on radial distribution systems[J].IEEE Transactions on Power Delivery,1989,4(1): 725-734.