考慮級間耦合高速多級圓筒型直線感應電機性能

關曉存 雷 彬 李治源 趙 然

（軍械工程學院三系 石家莊 050003）

1 引言

直線感應電機具有結構簡單、適應性比較強、特別適宜于高速運行等優點[1-3]，國內外都比較重視。直線感應電機可以按功能用途可分為:力電機、功電機和能電機。其中力電機主要應用于低速設備上，例如閥門的開閉、門窗的移動[4]等；功電機主要應用于長期連續運行的設備，例如高速磁懸浮列車[5]等；這兩種電機在國內已經有很多單位在研究，并且已經應用于日常生活中[6]。但能電機目前國內研究較少，能電機是指在短時間內所產生動能的驅動電機，主要性能指標是能效率[7]。在傳統直線感應電機中一般都有鐵心和繞組槽，電源一般都是三相380V供電；由于鐵心具有磁飽和現象，限制了加速力的大小[8-10]；而有繞組槽，增加了氣隙磁場的齒諧波，使得能效率降低[11-13]；三相供電加大了動子的加速力波動，使得動子在運行過程中不平穩[14-19]。為了提高能效率，圖1所示的高速多級圓筒型直線感應電機，在結構中去掉鐵心和繞組槽，并且使用電容器組供電，可以做到高壓驅動，特別適宜于高速發射領域。

圖1 電容器驅動高速長定子圓筒型直線感應電機二維示意圖Fig.1 Two dimensional model of HSMCLIM

2 考慮級間耦合電機磁場控制模型

由于該類型電機采用的是電容器組供電，并且電路中還有二極管等續流裝置，因此無法采用電機理論來分析該類型電機，所以從磁場、電路、運動耦合角度推導了該電機的數學模型。

為了建立多級長定子直線感應電動機的機電耦合模型，做如下假設:

（1）不考慮動子的橫向偏移，假定動子軸線中心和繞組中心重合，滿足軸對稱條件。

（2）不考慮動子在電磁力的作用下產生形變。

基于上述假設，當電樞運行在第1級區域且考慮級間耦合的第1級磁場控制方程

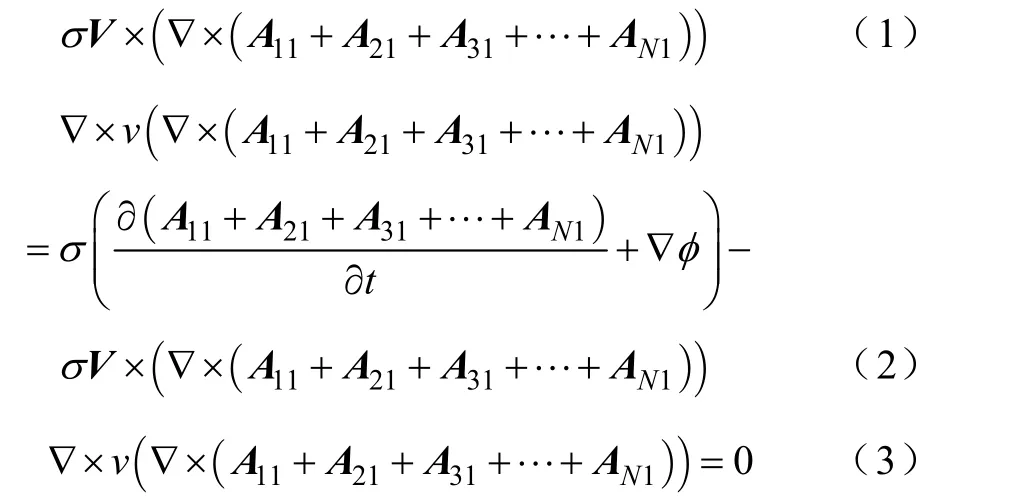
式中，11A 、V、1sJ 和φ 分別為第1級定子電流產生矢量磁位、動子的速度、不考慮級間耦合的第1級定子繞組時電流密度矢量和動子上的標量電位，其中φ?=0，可以消去；A21、A31、A41…AN1為各級定子繞組中電流在第1級定子繞組區域產生的矢量磁位；v和σ 分別為動子的磁阻率和電導率。

由于考慮級間耦合的影響，故第1級繞組區域的控制方程為式（1）；動子區域控制方程為式（2）；氣隙區域控制方程為式（3）。這樣就構成了考慮級間耦合的第1級定子磁場控制方程。

由此類推可以推導出考慮級間耦合高速多級長定子電機中第M級的磁場控制方程

式（4）～式（6）中不僅考慮了速度因素，還考慮了各級放電過程中的相互影響，這樣更準確地描述了高速多級圓筒型直線電機的瞬間運動狀態。

3 高速多級圓筒型直線電機的電路方程

高速多級圓筒型直線電機的等效電路模型如圖2所示。

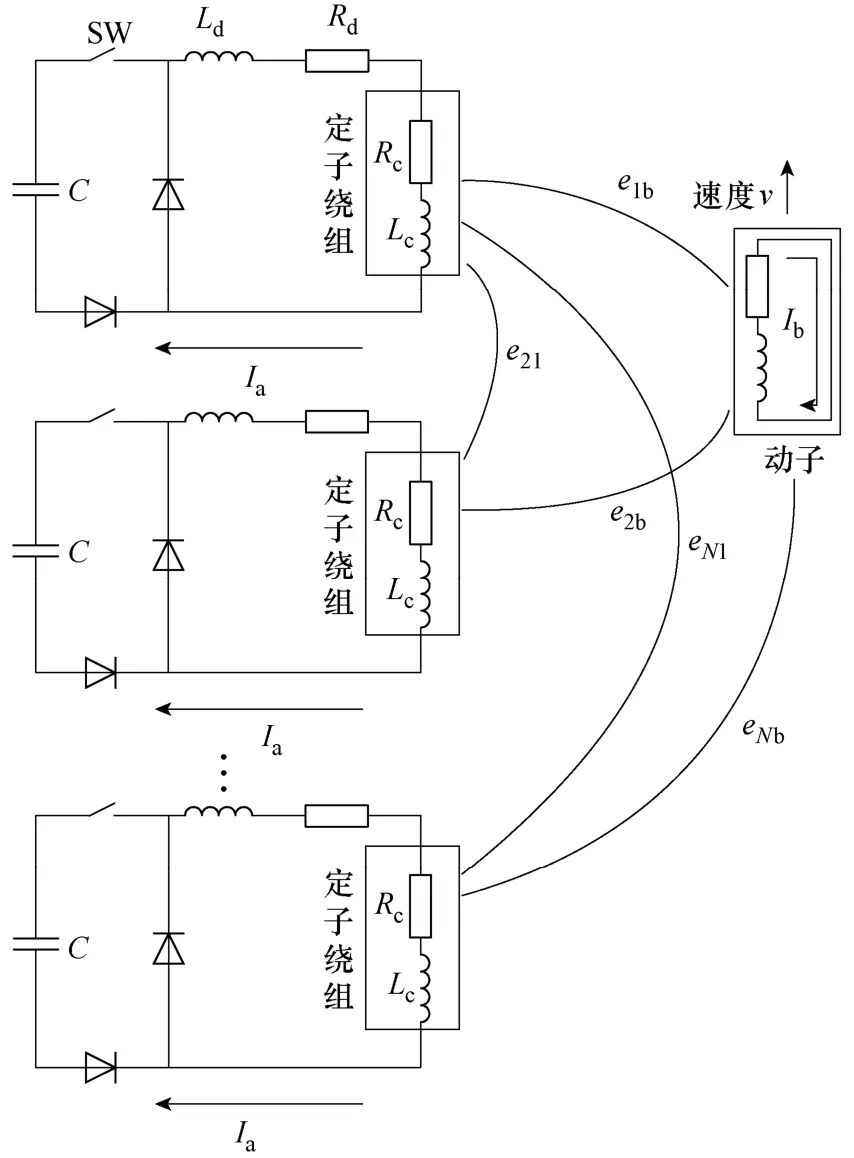
圖2 高速多級圓筒型直線電機簡化電路模型Fig.2 The equivalent circuit of HSMCLIM

由圖2可以寫成高速多級圓筒型直線電機的電路矩陣方程為式（7）。

式（7）中，Ri，Li，Ii分別為第 i級繞組的總電阻、總電感和電流，Ri=，Li=；Rb，Lb，Ib分別為動子的電阻、電感和電流。

電磁場方程和連接的電路方程相接口的中間環節驅動線圈和電樞中的電流及感應電動勢。其中，電流是整個求解系統的獨立狀態變量，而感應電動勢則是矢量磁位的函數，是非獨立狀態變量，因而整個場路方程耦合求解的關鍵是感應電動勢。有限元區的感應電動勢可通過與繞組所交鏈的磁通的變化來求得，而每個區域的磁通又是通過矢量磁位來求得的。下面以第N級定子繞組為例來說明感應電動勢和矢量磁位之間的關系，若第N級定子繞組每匝線圈的有效長度為L1，匝數為nc，且分了M個單元，Sc為繞組的橫截面積，g為單元的節點總數，則由此可得驅動線圈的電動勢為

同理可以得到其他級定子的感應電動勢e2，e3，e4，…，eN1，eb。

把上述感應電動勢代入式（7）可得式（8）。

式（8）可以簡寫為

式（6）、式（9）明確了各級定子電流之間的相互影響對各自電流大小的影響。從而影響著整個電機的運行性能。

4 高速多級圓筒型直線電機的控制策略

在高速多級圓筒型直線電機的設計過程中，為使其獲得較高動子線圈的速度需從以下幾個方面考慮:一是盡可能增大定子繞組和動子繞組之間的磁耦合系數；二是通過調整定子繞組和動子繞組的結構參數、電參數和動子繞組的初始發射位置及初始注入速度以獲得較理想的發射效率；三是通過確保各級定子繞組的饋電情況與動子繞組的運動位置保持同步，從而提高速度。

當高速多級圓筒型直線感應電機的結構參數確定時，第一種方法和第二種方法已經失效，因此，調整各級定子繞組的放電時間間隔來提高速度。設每一級定子繞組放電時間間隔為 t1，t2，t3…tN，動子繞組在每一級放電后所達到的速度為v1，v2，v3…vN，調整序列 t1，t2，t3…tN，使得

此時電機效率是最大的。圖3所示為各級定子繞組放電時間間隔的流程圖。

5 仿真與實驗分析

下面以10級圓筒型直線感應電機為例，來對比和分析考慮級間耦合（兩級相距較近）與不考慮級間耦合（兩級相距較遠）之間的不同。表1所示為各級定子及動子的結構參數。

圖3 各級放電間隔時間確定流程圖Fig.3 Flow chart of each stator discharge time-interval determination

表1 樣機的定子繞組和動子繞組的結構參數Tab.1 Structural parameter of prototype

其中定子繞組用外徑4φmm，內徑空心2φmm銅線繞制，兩極間距采用尼龍套筒相連；動子繞組用1φmm的銅線繞制，在尼龍棒上繞制，其負載質量為1kg。各級電容器組的電壓為15kV，電容值為1.2mF。圖4所示為10級圓筒型直線電機考慮級間耦合和不考慮級間耦合的各級定子繞組放電波形。如圖4a中所示，當考慮級間耦合時，根據最大效率控制策略尋找到各級放電時間為 0s、0.0003s、0.0005s、0.0006s、0.0007s、0.00075s、0.00085s、0.0009s、0.00095s、0.001s。這樣的電流波形不是規則的正弦半波，而且各自峰值和放電周期也不一樣，這主要是各級之間的耦合程度不同所造成的。圖4b所示為不考慮級間耦合的各級電流波形，其中級間放電間隔時間為0.001s，所以選擇0.001s是因為這時上一級的電流基本已經放電，不會在下一級產生影響。

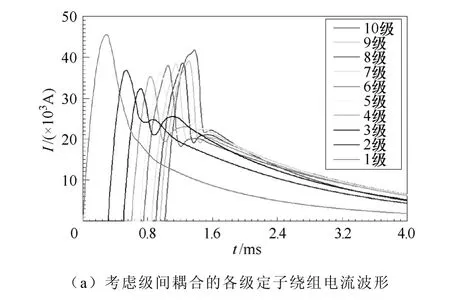
圖4 電機各級定子繞組電流曲線Fig.4 each stage stator current of HSMCLIM

圖4b中波形畸變是由于動子速度造成的。對比圖4a和圖4b可以看出級間耦合對電流影響很大。圖5為對比考慮級間耦合和不考慮級間耦合的加速力圖。如圖 5a中所示，加速力的平均峰值基本在700kN左右，而且持續時間大約為0.0015s，而負向峰值大約為100kN，持續時間為0.0001s。這樣情況下加速波形，使得動子受力恒定，加速度恒力，變形較小。而圖5b中，雖然各級峰值也在700kN，但總持續時間不長，且總的平均峰值小于700kN，動子受力波動很大，波動范圍基本是在0～700kN。這樣的加速波形，使得動子的結構變形很大，不利于高速發射。

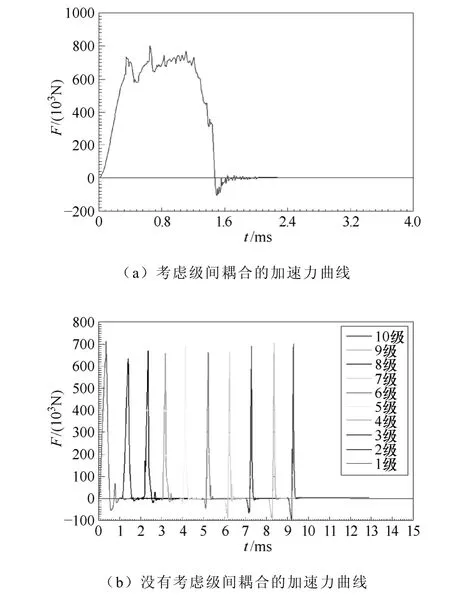
圖5 電機各級加速力曲線Fig.5 Accelerating force curve of HSMCLIM

圖6所示為兩種情況下動子所達到的速度曲線。圖6a中所示為動子在0.0015s能加速到800m/s，并且速度幾乎是以直線上升的；而圖6b中，動子在0.001s內加速到670m/s。這樣，電機能效率分別為23.7%和17.2%，說明級間耦合效應有利于提高電機的能效率。

圖6 電機動子速度曲線Fig.6 The armature speed curve of HSMCLIM

根據上面仿真結果分析，采用考慮級間耦合方式（兩級相距很近）來設計樣機，根據表1中各級定子繞組結構參數，制作了5級電容器驅動的圓筒型直線感應電機樣機，兩級相距10mm，如圖7所示。其中測電流的標準 Rogowski線圈靈敏度為50kA/1V，在級間的尼龍板上設兩個通孔，通孔內安裝有D2650—5—5型激光管，激光管發出的激光可經其對應的通孔內的光纖接受并傳輸至控制回路。開始發射時，動子繞組的前端剛好處于通孔處，一旦動子繞組開始運動，動子繞組將遮斷光路；當動子繞組的末端離開通孔時，光路自動接通。因此，在動子繞組經過通孔的過程中，光纖內將產生兩個光跳轉信號，利用示波器記錄這兩個跳轉信號之間的時間，就可求出動子經過該通孔的運動速度。

按照仿真所得出的各級放電時間間隔，設置 5級的放電時刻 0s、0.0003s、0.0005s、0.0006s、0.0007s，得到如圖8所示5級放電電流波形圖和表2所示各級末動子繞組的速度。

圖7 實驗樣機裝置及測量系統Fig.7 Experimental device and measurement system

圖8 各級定子繞組實驗電流結果Fig.8 Each stage stator experiment current

表2 實驗測得速度結果Tab.2 Experiment speed results

對比圖 8和圖 4，發現仿真計算結果的數值較大，這是因為仿真過程中連接導線、二極管內阻等沒有考慮，但波形吻合較好。如表2中所示，前5級的實際測量速度和仿真速度相比，仿真數值較大，而且隨著級數增加，實際測量數值和仿真數值相差越來越大，其原因為上述得到的各級放電時間間隔是仿真中得到的結果，而實際各級末速度較小，由于誤差累積，這樣就會造成上述的放電時間間隔不是最優的，應該在仿真結果基礎上進行微調。

6 結論

本文基于電磁場基本理論，指出高速多級圓筒形直線感應電機工作特點，推導出該電極考慮級間耦合的運行數學模型，并利用此模型分析了10級電機中級間耦合對定子電流、動子加速力和速度、電機能效率的影響，并與忽略級間耦合時電機的結果進行對比。結果表明該電機各級定子之間應該設計緊湊，充分利用級間耦合效應，使得電機運行平穩，效率更高。最后，通過對圓筒形直線感應電機樣機實驗，測得各級中動子所獲的速度，并將實驗結果與仿真分析結果進行比較，二者吻合很好。

[1]葉云岳.直線驅動裝置與系統[M].北京: 冶金工業出版社, 2002.

[2]葉云岳.直線電機技術手冊[M].北京: 機械工業出版社 2003.

[3]龍遐令.直線感應電動機的理論和電磁設計方法[M].北京: 科學出版社, 2006.

[4]葉云岳.遙控直線電機驅動的窗簾機的設計與應用[C].全國中小型電機學術年會, 1991: 46-50.

[5]劉華清, 等.德國磁懸浮列車 Transrapid[M].成都:電子科技大學出版社, 1995.

[6]山田一.直線電機及應用技術[M].湖南: 湖南科學技術出版社, 1979.

[7]Sakae Yamamura.Theory of linear induction motors[M].Tokyo: University of Toyko Press, 1972.

[8]上官璇峰, 勵慶浮, 等.不連續定子永磁直線同步電動機運行過程分析[J].西安交通大學學報, 2004,12(38): 1292-1295.Shangguan Xuanfeng, Li Qingfu, et al.Analysis on running process of permanent linear synchronous motors with discontinuous stators[J].Journal of Xi’an Jiaotong University, 2004, 12(38): 1292-1295.

[9]上官璇峰, 勵慶浮, 等.多段初級永磁直線同步電動機驅動系統整體和仿真[J].電工技術學報, 2006,21(3): 52-57.Shangguan Xuanfeng, Li Qingfu, et al.Integrated modeling and simulation of the system driven by multi-segment primary permanent linear synchronous motors[J].Transactions of China Electrotechnical Society, 2006, 21(3): 52-57.

[10]上官璇峰, 勵慶浮, 等.多段初級永磁直線同步電機驅動的垂直提升系統[J].中國電機工程學報,2007, 27(18): 7-12.Shangguan Xuanfeng, Li Qingfu, et al.The vertical hoist system driven by PMLSM with multi-segment primary[J].Proceedings of the CSEE, 2007, 27(18):7-12.

[11]Onuki T, Kamiya Y, Kurimoto Y, et al.A novel block feeding method in the single-sided LIM with a short secondary member[J].IEEE Transactions on Energy Conversion , 1999, 14(4): 1323-1328.

[12]Davey K.Predicting induction motor circuit parameters[J].IEEE Transactions on Magnetics, 2002,38(4): 1774-1779.

[13]Van Zyl A W, Landy C F.Reduction of cogging forces in a tubular linear synchronous motor by optimizing the secondary design[C].IEEE African Conference, 2002: 284-288.

[14]魯軍勇, 馬偉明, 許金.高速長定子直線感應電動機的建模與仿真[J].中國電機工程學報, 2008,28(27): 89-94.Lu Junyong, Ma Weiming, Xu Jin.modeling and simulation of high speed long primary double-sided linear induction motor[J].Proceedings of the CSEE,2008, 28(27): 89-94.

[15]魯軍勇, 馬偉明, 李朗如.高速長初級直線感應電動機縱向邊端效應研究[J].中國電機工程學報,2008, 28(30): 73-78.Lu Junyong, Ma Weiming, Li Langru.Research on longitudinal end effect of high speed long primary double-sided linear induction motor[J].Proceedings of the CSEE, 2008, 28(30): 73-78.

[16]盧琴芬, 方攸同, 葉云岳.大氣隙直線感應電機的力特性分析[J].中國電機工程學報, 2005, 25(21):132-136.Lu Qinfen, Fang Youtong, Ye Yunyue.A study on force characteristic of large air gap linear induction motor[J].Proceedings of the CSEE, 2005, 25(21):132-136.

[17]張永, 徐善綱.次級分段直線磁阻電動機的分析[J].中國電機工程學報, 1999, 19(9): 62-65.Zhang Yong, Xu Shangang.Analysis of segmental secondary linear reluctance motor[J].Proceedings of the CSEE, 1999, 19(9): 62-65.

[18]He J L, Zabar Z, Levi E, Birenbaum L.Analysis of induction-type coilgun performance based on cylindrical current sheet model[J].IEEE Transactions on Magnetics, 1991, 27(1): 379-584.

[19]Andrews J A, Devine J R.Armature design for coaxial induction launchers [J].IEEE Transactions on Magnetics, 1991, 27(1): 639-643.