一種采用螺旋耦合環的同軸腔可調濾波器

張忠海 官伯然

(1.西安電子科技大學電子工程學院，陜西 西安710071； 2.杭州電子科技大學天線與微波技術研究所，浙江 杭州 310018)

1. 引 言

濾波器是通信設備中的關鍵部件，現代通信設備的便攜性和高頻譜利用率要求給濾波器設計帶來新的挑戰[1-3]。對于可調濾波器，這種挑戰包括小型化，在全部可調范圍內帶寬不變和高功率容量等[4-10]。有多種技術可以設計實現可調濾波器，包括可調電容加載的低溫共燒陶瓷(LTCC)濾波器[1]，可調電容加載的微帶濾波器[2-3]，同軸腔濾波器[4-7]等。在文獻[8]和[9]中，給出了兩種設計基于變容二極管的可調濾波器設計方法。基于這兩種方法的可調帶通濾波器能夠實現全工作頻段內通帶帶寬的差別小于5%。但是，這兩種濾波器的功率容量有限，帶外隔離特性也比較差。同軸諧振腔可調濾波器由于其高功率容量和高Q值特性而引起人們的關注并獲得廣泛應用[1，6，7，10]。

同軸腔濾波器通常采用四分之一波長同軸腔作為基本諧振單元，其腔間耦合利用腔體之間的矩形或者圓形耦合窗口實現[6-7]。通過調節耦合窗口的位置及軸向長度，能夠減小可調濾波器在工作頻段內的高低端帶寬差別[6]。然而，窗口軸向尺寸的加大最終會導致濾波器的體積變大，從而不能滿足小型化可調濾波器的設計要求[6]。可調電容加載的同軸腔諧振器通常用來縮小可調濾波器的體積。但是，同軸腔諧振器尺寸的縮小也會導致耦合窗口軸向尺寸的縮小，進而導致同軸腔濾波器的高低端帶寬差別變大。由以上的分析可知，僅采用耦合窗口實現腔間耦合會導致可調濾波器的帶寬隨調諧頻率發生變化，通帶帶寬隨調諧頻率的增加而變大。這種現象對可調頻率范圍比較寬的帶通濾波器尤為嚴重[4]。

本文提出了一種采用新型腔間耦合結構的同軸腔可調濾波器。該濾波器采用電容加載以縮小可調濾波器的體積，其長度僅為170 mm，小于中心頻率(320 MHz)的四分之一波長。文獻[6]中的濾波器長度大于二分之一波長。本文提出的可調濾波器腔間耦合結構由矩形耦合窗口和螺旋耦合環組成，采用這種腔間耦合結構的可調濾波器能夠在整個工作頻段內(230～410 MHz)具有幾乎不變的帶寬。此外，螺旋耦合環的加入同時改善了可調濾波器的插入損耗和紋波，并使濾波器的調整更加容易。

2.理論分析

2.1 同軸腔可調濾波器帶寬變化分析

對于同軸腔可調濾波器，影響其工作頻段內的絕對帶寬的因素主要是腔間耦合以及輸入輸出耦合，而這兩種耦合都會隨頻率的變化而變化。

首先分析腔間耦合對同軸腔可調濾波器的影響。對于經典的同軸腔濾波器，磁場耦合起絕對作用。耦合的磁通量越多，則腔間耦合系數越大，實現的腔體濾波器的帶寬就越大。一般通過腔間的矩形或者是圓形耦合窗口來實現腔間磁耦合，通過調整耦合窗口的大小和位置可以調節耦合帶寬的大小。對于中心頻率在一定頻率范圍內變化的可調濾波器，頻率的變化會帶來同軸腔內磁場分布的變化，由此引起耦合系數的變化，即帶寬會發生變化。因此，分析可調濾波器的帶寬變化首先要分析不同頻率下同軸腔內磁場分布的變化。

對于四分之一波長同軸腔，其內部的電磁場分布為[11]。

(1)

式中：a為同軸腔內導體外徑；η是空氣波阻抗。

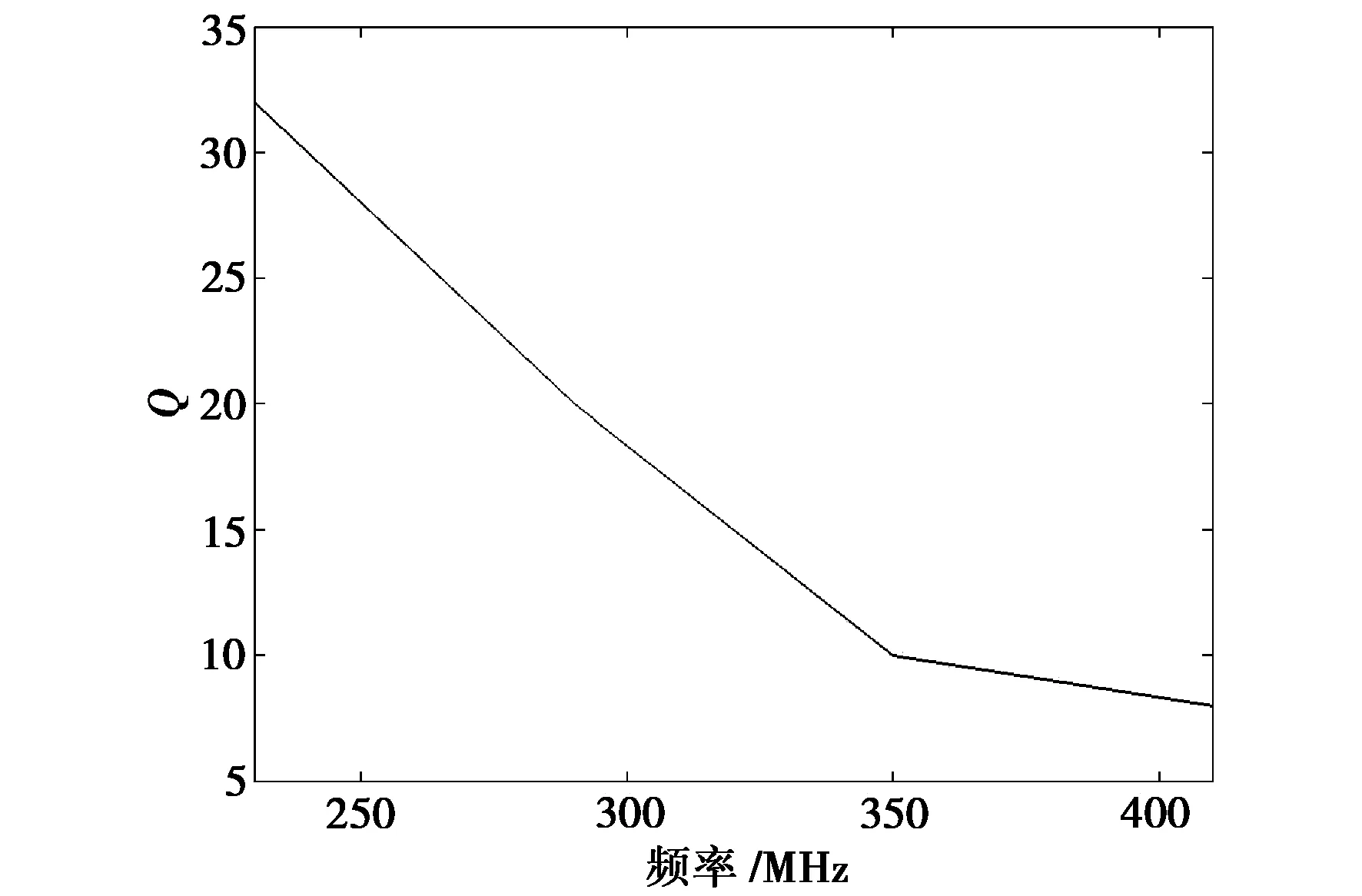
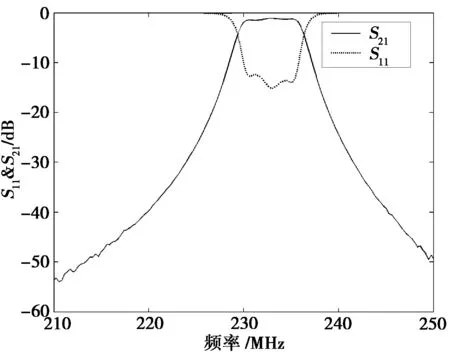
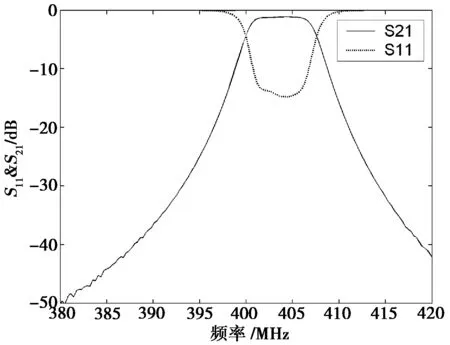
調節同軸腔的加載電容，令同軸腔諧振于兩個頻率f1和f2，f1

(2)

式中：H01對應f1；H02對應f02。

文中設計的濾波器調諧頻率范圍為230～410 MHz。由公式(2)可以得出兩個頻率下同軸腔距短路端120 mm以內的磁場分布如圖1所示：

圖1 不同頻率情況下四分之一同軸腔內磁場歸一化幅度沿軸向變化曲線

由圖1可以看出，對于給定的高低端頻率，短路端的磁場強度都是最大的，然后沿軸向逐漸減小。在短路端，高頻端的磁場強度大于低頻端的磁場強度，但是頻率較低的時候磁場沿軸向下降較緩，頻率高的時候則下降較快。在距離短路端99 mm處，高頻端磁場強度和低頻端磁場強度相等。在此之后，高頻磁場強度就小于低頻磁場強度。因為耦合磁通量的大小和耦合系數有直接的關系，耦合的磁通量多耦合系數就大，反之就小。由此可以得到結論：如果耦合窗口足夠長，并且中心位置在距離短路端99 mm附近，可以做到低頻和高頻的耦合系數相等，甚至低頻端的耦合系數大于高頻端的耦合系數。但是對于小型化的電容加載可調同軸腔濾波器來說，耦合窗口軸向長度由于空間限制通常小于八分之一波長，而且為了保證帶寬和差損的指標耦合窗口的起始位置通常置于短路端，所以僅采用腔間耦合窗口的耦合方式將會導致高頻端的耦合系數大于低頻端的耦合系數。

在四分之一波長同軸腔濾波器的設計過程中，可以利用高頻電磁仿真軟件(HFSS)，電磁仿真軟件(CST)等高頻仿真軟件來確定耦合窗口的耦合帶寬和頻率的關系。固定耦合窗口的尺寸和位置，矩形耦合窗口的耦合帶寬隨頻率的變化如圖2所示。其中，矩形耦合窗口從短路端開始，長120 mm，寬34 mm.

圖2 矩形耦合窗口的耦合帶寬隨頻率變化曲線

如圖2所示，濾波器的帶寬隨著頻率的升高而升高。在230～410 MHz這個工作頻率范圍內，對于矩形耦合窗口，可調濾波器的帶寬從1.8 MHz 增大到3.57 MHz，有±198%的差別。此時，耦合窗口的長度為100 mm，寬度45 mm.

同軸腔濾波器中通常采用將同軸連接器內導體與同軸腔內導體相連接做為輸入輸出耦合方式，其連接位置可以根據可調濾波器的有載Q值確定，有載Q值與濾波器帶寬之間的關系為

(3)

式中：f0是濾波器的中心頻率；g1是低通原型值；BW是濾波器的帶寬。由式(3)可知，如欲保持可調同軸腔濾波器的絕對帶寬不變，則要求濾波器的輸入輸出端口的有載Q值隨濾波器工作的中心頻率增大而增大。固定同軸連接器內導體與同軸腔內導體連接位置，可調濾波器的有載Q值隨著頻率的變化曲線如圖3所示。由圖3可知，隨著頻率的升高，可調濾波器的輸入輸出有載Q值變小。根據公式(3)，在頻率增加，輸入輸出有載Q值減小的情況下，會導致濾波器帶寬增大，從而，可調濾波器的高低端帶寬差進一步惡化。

圖3 可調濾波器輸入輸出有載Q值隨著頻率的變化曲線

2.2 采用螺旋耦合環和耦合窗口結合的濾波器

由圖2和圖3可以看出，僅僅采用耦合窗口的可調濾波器，隨著頻率的升高濾波器的帶寬也隨之增加。為了平衡高低端帶寬，同軸腔濾波器的腔間耦合結構設計需要滿足在減小高頻端耦合磁通量的同時增加低頻端耦合的磁通量的要求。為了滿足這個要求，要求腔間耦合窗口中心能覆蓋圖1中99 mm處的位置，并且盡量包括高頻磁場強度小于低頻磁場強度的位置，即99～110 mm之間的位置。但是因為濾波器的尺寸所限，耦合窗口不可能太長，本文中設計的小型化濾波器能夠允許的耦合窗口最長只能110 mm。同時為了滿足濾波器的帶寬要求，耦合窗口需要覆蓋短路端。本文采用在耦合窗口中插入螺旋耦合環來保證帶寬，并實現在可調濾波器全工作頻段內通帶帶寬保持不變的目標。采用螺旋耦合環的3腔同軸腔濾波器結構如圖4所示。可調濾波器帶寬由螺旋耦合環和矩形耦合窗口共同確定。采用螺旋耦合環的可調濾波器耦合帶寬的HFSS仿真結果如圖5所示。由圖5可知，在工作頻率230～410 MHz內，濾波器的帶寬從6.47 MHz變化到6.52 MHz，帶寬變化小于±0.7 %。

圖4 采用螺旋耦合環的3腔同軸腔濾波器結構圖

圖5 采用螺旋耦合環的濾波器耦合帶寬隨頻率的變化

3.實驗結果分析

根據上面的分析，設計并且制作了采用矩形耦合窗口結合螺旋耦合環的3腔同軸腔可調濾波器。確定螺旋耦合環的尺寸的方法與確定矩形窗口的方法相似。螺旋耦合環的耦合帶寬隨尺寸變化的曲線可以通過電磁仿真工具得到，并根據仿真結果提取所需要的尺寸。本文所設計的同軸強可調濾波器長170 mm，矩形窗口長110 mm，螺旋耦合環長95 mm，螺旋部分的寬度38 mm，長度35 mm，螺距2 mm。可調帶通濾波器工作于230 MHz至406 MHz范圍內。可調濾波器高低端傳輸特性的測試結果分別如圖6和圖7所示。

圖6 采用螺旋耦合環同軸腔可調濾波器的低端傳輸特性測試曲線

圖7 采用螺旋耦合環同軸腔可調濾波器的高端傳輸特性測試曲線

由圖5中可知：采用螺旋耦合環的同軸腔可調濾波器的耦合帶寬隨頻率的變化不是嚴格的常數，所實現的可調濾波器的帶寬在整個頻段內會有一些差別。

由圖6和圖7得出，該濾波器的3 dB帶寬在低頻端為6.4 MHz，在高頻端為6.5 MHz，帶寬差為1.5%。在230 MHz處的通帶插入損耗為1.1 dB，在406 MHz處的通帶插入損耗為1.0 dB。

采用矩形耦合窗口結合螺旋耦合環的可調同軸腔濾波器的帶寬是矩形窗口和螺旋耦合環共同的貢獻，在矩形耦合窗口中插入螺旋耦合環可以平衡濾波器的高低端帶寬。同時，因為增加了腔間耦合，可調濾波器的帶寬也有所增加。如果僅采用矩形耦合窗口，因窗口軸長受腔體尺寸的限制，窗口覆蓋區域中高頻磁場強度小于低頻磁場強度的區域很小，無法平衡高低端帶寬。由于螺旋耦合環能實現腔間輔助耦合，并且在設計中使其覆蓋99 mm到110 mm區域，能夠達到平衡高低端帶寬的目的。

圖6中可調濾波器的低頻端帶內紋波比圖7中高頻端的帶內紋波大，這是因為設計實現的可調濾波器的帶寬比較大，因此，低頻端耦合還略顯不足。加長矩形耦合窗口的長度或者增加螺旋耦合環的圈數都可以增加低頻端的耦合，減小低頻端的帶內紋波。

如果設計的可調濾波器的帶寬較窄，則可以將矩形耦合窗口的起始位置向同軸腔的開路端移動，同時借助螺旋耦合環，則可更加容易平衡濾波器的高低端帶寬。

因為加工精度的原因導致測試的可調濾波器的高端頻率比設計預期值略低。本文中的濾波器采用電容膜片結構的調諧機構，而為了實現小型化可調濾波器，需要加載大電容，所以，這種電容膜片之間的距離比較小，需要很高的加工精度。在實際的應用過程中，只要將設計的頻率范圍高低端都延展10 MHz，就能補償加工精度帶來的頻率偏移，不影響實際應用。

4.結 論

提出了一種耦合窗口結合螺旋耦合環的耦合結構。采用這種結構的可調濾波器可以在整個工作頻段內保持幾乎不變的帶寬。同時改善了可調濾波器插入損耗。螺旋耦合環的加入給可調濾波器增加了可調量，從而使可調濾波器更加容易調整。采用這種結構可調濾波器可以根據需要在一定范圍內調節帶寬而無需重新加工昂貴的腔體。這種耦合結構適用于小型化的同軸腔可調濾波器設計中。

[1] 墨晶巖，馬哲旺. 低溫共燒陶瓷(LTCC)四級低通濾波器設計[J]. 電波科學學報, 2005, 20(5): 566-569.

MO Jingyan, MA Zhewang. Design of an LTCC four-pole lowpass filter with two transmission zeros in its stopband[J]. Chinese Journal of Radio Science, 2005, 20(5): 566-569. (in Chinese )

[2] 彭 毅，章文勛. 應用交指電容加載環諧振器的微帶帶阻濾波器[J]. 電波科學學報,2009, 4(5):909-913.

PENG Yi, ZHANG Wenxun. Compact microstrip band-stop filter using interdigital capacitance loading loop resonator[J]. Chinese Journal of Radio Science, 2009, 4(5):909-913. (in Chinese)

[3] 付淑洪，童創明，李西敏. 一種新穎的開口環地面缺陷結構低通濾波器[J]. 電波科學學報，2009, 24(6):1115-1118.

FU Shuhong, TONG Chuangming, LI Ximin. A novel split-ring resonator defected ground structure lowpass filter[J]. Chinese Journal of Radio Science, 2009, 24(6):1115-1118. (in Chinese)

[4] 熊瑩霞. 可調腔體帶通濾波器的研究與設計[D]. 上海： 華東師范大學，2005.

[5] KURZROK R M. Design of Interstage Coupling Apertures for Narrow-Band Tunable Coaxial Band-Pass Filters[J]. IEEE Trans. Microwave Theory Tech, 1962, 10(2): 143-144.

[6] 姚 毅，賈金玲.四腔同軸調諧微波濾波器的研制[J]. 四川輕化工學院學報，1997，10(1): 1-7.

YAO Yi, JIA Jinling. The Development of A Coaxial Tunable Microwave Filter of Four Cavities[J]. Journal of Sichuan Institute of Light Industry and Chemical Technology, 1997，10(1): 1-7. (in Chinese)

[7] 朱華彬，漆蘭芬.多腔體射頻可調諧濾波器的研究[J]. 華中科技大學學報(自然科學版)，2003，31(2):87-89.

ZHU Huabin,QI Lanfen. The study of multiple2cavity RF tunable filter[J]. Huazhong Univ. of Sci. & Tech. (Nature Science Edition), 2003，31(2):87-89. (in Chinese)

[8] ESTES J C. TUNABLE R F. Bandpass Pass Filter with Variable Resonator Coupling[C]. IEEE MTT-S Int. Microwave Symp.Dig. 2008: 1035-1038.

[9] PARK S J, REBEIZ G M. Low-loss two-pole tunable filters with three different predefined Bandwidth Characteristics[J]. IEEE Trans. Microwave Theory Techn. 2008, 56(5): 1137-1148.

[10] 韓世虎，王錫良，樊 勇. 廣義切比雪夫濾波器耦合矩陣的優化提取[J]. 電波科學學報，2007, 22(1):153-157.

HAN Shihu, WANG Xiliang, FAN Yong. Optimization method for extracting coupling matrix of generalized chebyshev filter[J]. Chinese Journal of Radio Science, 2007, 22(1):153-157. (in Chinese)

[11] 梁昌洪，謝擁軍，官伯然. 簡明微波[M]. 北京：高等教育出版社，2006：145-146.