工序能力指數標準化定義之應用(雙側限)

于善奇 安 軍

工序能力指數標準化定義之應用(雙側限)

于善奇 安 軍

在雙側規范的情形下,研究了工序能力指數標準化定義的依據;在以不合格品率(p)為質量指標的情形下,不僅證明了p與CP、ε(偏移量)之間的計算公式,而且給出詳盡的數值表。此外,還給出了典型的應用示例,供企業參照。

雙側限 工序能力指數 標準化 數值表

1 雙側限工序能力指數標準化定義的依據

加工過程的偏移量ε=|μ-M|。

1.1 工序無偏的情形

當工序無偏時,即偏移量 ε=|μ-M|=0,雙側限工序能力指數的標準化定義[1]為

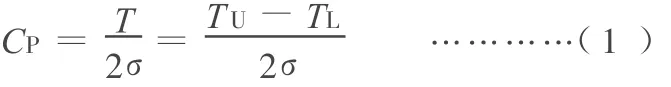
由于TU-M=M-TL,注意到 ε=0,即 μ=M時,TU-TL可改寫為

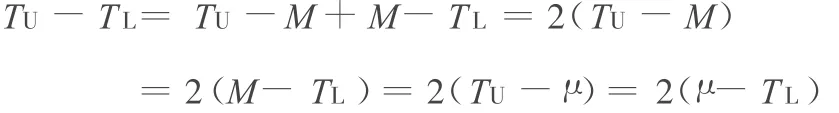
于是,式(1)可改寫為

當工序有偏時,偏移量 ε=|μ-M|≠0,雙側限工序能力指數的標準化定義為

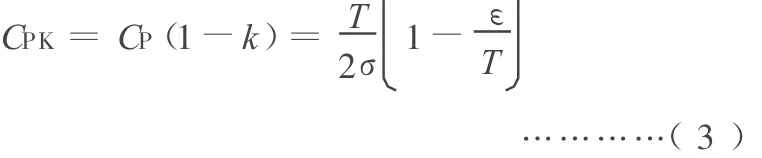
2 在雙側限工序能力指數的標準化定義下,產品質量的分析

2.1 工序無偏的情形

在工序無偏的情形下,注意到式(2),加工過程的不合格品率p與CP間的關系為

2.2 工序有偏的情形

根據式(5),若給定偏移量ε=a·a(這里的系數a為實數,比如 α=1.5,表示偏移 1.5σ),不難得出p與CP間的數值表。顯而易見,當 ε=0時,式(4)是式(5)的特例。限于版面,本文僅給出CP值和偏移量ε的常用變化范圍,其中CP的步長為0.1,ε的步長為0.05σ,參見表1。必須指出,有的企業不是根據實際偏移狀態,一律按偏移1.5σ分析產品質量,是不妥當的。此外,對某一特定企業而言,根據CP值的特定變化范圍和偏移量的大小,可以利用式(5)將數值表細化。

表1 不合格品率 p與CP、ε間數值表(雙側限)

續表1

2.3 應用示例

例1.某產品某項特性的規范上限TU=5.02(mm),規范下限TL=4.98(mm),規范中心M=5.00(mm)。已知加工過程穩定,該工序長期統計結果表明,均值 μ=5.008(mm),標準差 σ=0.0051(mm)。試確定該工序的CP值和加工過程的不合格品率。

解： 先求標準化定義的CP值。這是雙側限的情形,已知標準差σ=0.0051,公差T=TU-TL=0.04,所以

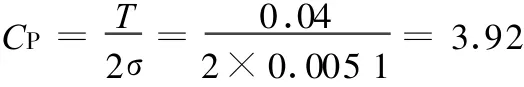
由于偏移量 ε=|μ-M|=0.008,σ=0.0051,所以 ε=1.57σ。具備一定基礎的讀者,不難依據式(5)計算得到

不具備一定基礎的讀者,可以查表1得出近似結果。

例2.采用某種設備灌注瓶裝酒,標準規定每瓶酒凈重(500±2)mL,平均凈重M=500(mL)。某天上午10點隨機抽測8瓶酒,測得樣本均值ˉx=500.5(mL),樣本標準差S=0.482(mL)。試分析該工序的CP值和瓶裝酒的不合格品率。

解： 先求標準化定義的CP值。由于樣本量n=8,樣本標準差S=0.482,所以標準差 σ的無偏估計值為

其中C4稱為修偏系數,其值參見表2[2]。已知產品公差T=4,于是CP值為

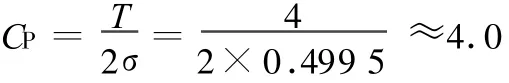
又偏移量ε=|μ-M|≈0.5,≈0.4995,故ε≈1.0,查表1可知,當CP=4.0,ε=1.0σ時,瓶裝酒的不合格品率p=1350×10-6。

表2 正態分布標準差的修偏系數C4

3 在雙側限工序能力指數的標準化定義下,CP值的評級參考

在雙側限工序能力指數的標準化定義下,CP值的評級參考見表3。

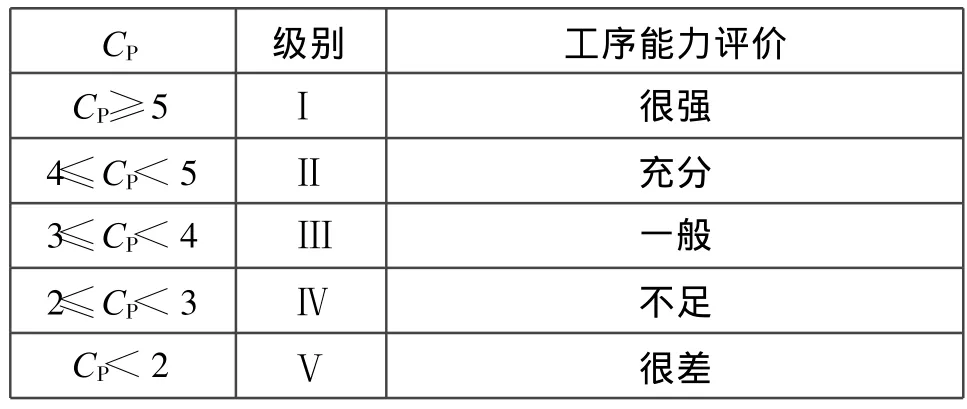
表 3 CP值的評級參考(雙側限)

需要指出,表3中CP值的評價僅是籠統性提法。CP值的大小取決于SMIE,其中最主要的因素是加工設備的精度和原材料的質量水平,其次是操作者的技術水平及工藝方法等因素的影響,這些因素可歸納為技術與管理兩大類。比如,對Ⅱ級加工的評價是技術與管理能力都很好,應繼續維持;對Ⅲ級加工的評價是技術與管理能力一般,不是很好,應設法提高到Ⅱ級。一般說來,Ⅰ級加工適用于電子行業;Ⅱ級加工適用于機械行業;Ⅲ級加工適用于化工類行業。

[1]于善奇.工序能力指數全新定義的探討[J].標準科學,2009(2)：9-10.

[2]于善奇.質量專業常用統計技術[M].華齡出版社,2003：70-71.