一種基于虛擬力的有向傳感器網絡低冗余覆蓋增強算法*

黃 帥，程良倫

(廣東工業大學自動化學院，廣州510006)

隨著監測環境的日趨復雜多變，由傳統傳感器網絡所獲取的簡單數據愈加不能滿足人們對環境監測的全面需求，迫切需要將數據量大、內容豐富的圖像、視頻等媒體引入到以傳感器網絡為基礎的環境監測活動中來，實現細粒度，精準信息的環境監測[1]。針對這種需求，作為傳感器網絡高級形式的有向傳感器網絡應運而生，它主要包括視頻傳感器網絡和圖像傳感器網絡。有向傳感器網絡的性能主要通過在監測區域內部署的傳感器節點的覆蓋率來體現[2]，因此優化有向傳感器網絡的覆蓋對于合理分配網絡的空間資源，更好地完成環境感知、信息獲取任務以及提高網絡的生存能力都具有重要的意義。但是由于有向傳感器網絡中傳感器節點受視場限制，不能和傳統傳感器網絡中的節點一樣采用全向感知模型，因此有向傳感器網絡的覆蓋問題相對于傳統的傳感器網絡的要復雜許多。

目前，國內外已有很多學者[3－7，12]針對有向傳感器網絡的覆蓋增強問題作了深入的研究。Ma等人在文獻[3]中提出了一種2D感知模型并研究了有向傳感器網絡覆蓋完整性以及通信連通性問題。在此基礎上，文獻[4]進一步提出了一種基于圖論和計算幾何的集中式覆蓋增強算法，但是由于未能充分考慮到有向傳感器節點局部位置及傳感方向信息，該算法對有向傳感器網絡覆蓋增強的能力相對有限。文獻[5]設計了一種方向可調感知模型，并以此為基礎提出了一種基于虛擬勢場的有向傳感器網絡覆蓋增強算法，巧妙的引入“質心”概念，將有向傳感器網絡的覆蓋增強問題轉化為質心均勻分布問題，以質心點作圓周運動代替節點傳感方向的轉動，達到消除網絡中感知重疊區和盲區，增強網絡覆蓋的目的。文獻[6]提出了一種基于虛擬勢場的路徑覆蓋增強算法，將要解決的問題轉化為質心點－運動軌跡點，質心點－質心點之間的虛擬力作用情況，以較小的代價獲得了視頻傳感器網絡對路徑的充分覆蓋，但是存在一個問題:當軌跡點對傳感器節點的引力和其它傳感器節點對該傳感器節點的斥力合力為零時，此時如果該傳感器節點和周圍傳感器節點存在大量共同的軌跡覆蓋點，則該傳感器節點并沒有發揮軌跡點的有效覆蓋功能，網絡會陷入局部最小情況。文獻[7]針對文獻[6]存在的問題提出了一種基于改進勢場的有向傳感器網絡路徑覆蓋增強算法，通過將相鄰傳感器節點對路徑軌跡點的共同覆蓋率引入到斥力計算中，有效引導節點的主感知方向調整，從而達到路徑的高效覆蓋。

傳統基于虛擬力的覆蓋增強算法只判斷調整方向，節點的調整量為固定值，并且沒有解決整個網絡進入穩定狀態后的冗余覆蓋問題。本文在設計出方向可調感知模型后，提出一種基于虛擬力的有向傳感器網絡低冗余覆蓋增強算法，建立虛擬力與角度調整量之間的關系模型，根據虛擬力的大小改變節點的角度調整量;當虛擬力小于某個閾值后，說明節點此刻進入了穩定狀態，計算節點覆蓋子集的集合，如果存在除了此節點以外的覆蓋子集，則通知其中一個覆蓋子集中包含的節點停止調整，同時此節點進入休眠狀態。最后通過仿真實驗證明算法的有效性，提高了有向傳感器網絡的調整效率，并且在保證覆蓋率的前提下很好的解決了網絡中的覆蓋冗余問題。

1 有向傳感器網絡冗余覆蓋增強問題

1．1 有向傳感器節點的方向可調感知模型和覆蓋子集

如圖1所示，有向傳感器節點的方向可調感知模型采用五元組 ＜P，R，V(t)，α，β＞來表示。其中P(x，y)表示節點的位置坐標;R表示節點的有效感知半徑;V(t)=(Vx(t)，Vy(t))為節點在時刻t的感知方向;2α表示節點的有效感知角度;β表示節點感知方向的角度調整量。

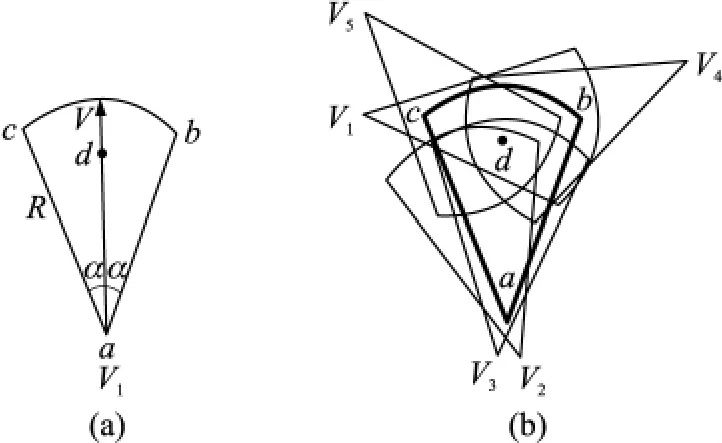
圖1 有向傳感器節點的覆蓋模型

在增強過程中，網絡中的每個節點都明確自身的覆蓋范圍，而它所覆蓋的范圍也可能由網絡中的其它幾個鄰居節點所覆蓋。

定義1定義集合Coi(v)為有向傳感器節點v的一個覆蓋子集，其中UV'∈Coi(v)可以覆蓋有向傳感器節點v的覆蓋區域。

定義2定義Co(v)為覆蓋節點v覆蓋區域的所有覆蓋子集的集合。

為了計算Co(v)，需要定義4個點(三個定點以及重心)來標識節點v的覆蓋區域，如圖1(a)所示。若Coi(v)∈Co(v)覆蓋節點v所覆蓋的區域成立，當且僅當滿足以下條件:

(1)?v'∈Coi(v)，v'覆蓋點 d 以及{a，b，c}中至少一個點。

(2)Coi(v)可以覆蓋 a、b、c、d 四個點。

1．2 有向傳感器網絡低冗余覆蓋增強問題的分析

在做本文的研究之前，做出以下假設:

(1)有向傳感器網絡中部署的所有節點均同構，即所有節點的感知半徑、傳感夾角等參數都一樣;

(2)在進行覆蓋增強的調整過程中，所有節點位置不變，但其傳感方向可調;

(3)有向傳感器網絡中各節點均明確其自身位置以及傳感方向，并能對自身的傳感方向進行調節，但是此調節僅限制于圍繞固定點做圓周運動。

(4)有向傳感器網絡中節點的受力點為其方向可調感知模型的質心。

如圖1(b)所示，節點 v的覆蓋區域由 a、b、c、d四個點表示，可以找到滿足條件的覆蓋子集有AG={v2，v1}，BG={v3，v1}，CG={v1，v5}。根據前面提到的方法，節點v的覆蓋子集的集合為:

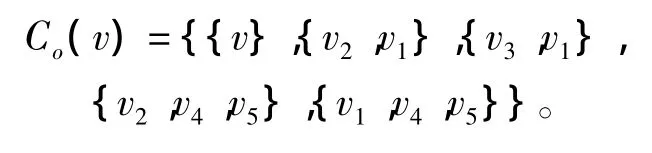
當某個節點進入穩定狀態后，計算此節點的覆蓋子集的集合，如果存在除了此節點以外的覆蓋子集，則通知其中一個覆蓋子集中包含的節點停止調整，此節點進入休眠狀態。

設Ai(t)表示節點vi在傳感向量為V(t)時的感知面積，Ai(t)∪Aj(t)表示節點vi和節點vj的感知面積進行并運算后得到的總面積。當網絡中節點的傳感向量分別為(V1(t)，V2(t)，V3(t)，…，VN(t))時，有向傳感器網絡的覆蓋率表示如下[5]:

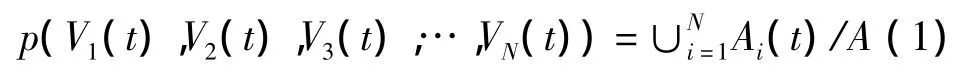
其中，A表示監測區域的面積。

在一個監測區域內分布了N個結構相同的有向傳感器節點，則區域覆蓋增強算法可以看作一個求最優解的問題，即求解一組(V1(t)，V2(t)，V3(t)，…，VN(t))*，使得對于所有(V1(t)，V2(t)，V3(t)，…，VN(t))式(2)成立:

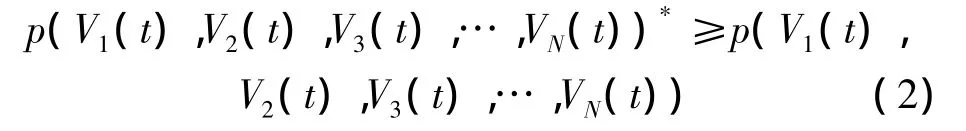
2 有向傳感網絡低冗余覆蓋增強算法

2．1 虛擬力的建立以及合力的計算

虛擬勢場(Potential Force)方法是解決傳感器網絡覆蓋控制問題的典型方法之一[5]，許多關于傳感器網絡覆蓋問題的文獻[6－10]都采用了這種思想，假定傳感器節點之間存在一種虛擬的斥力，而傳感器節點與監測目標之間又存在一種虛擬的引力，通過這兩種虛擬力的抗衡達到增強網絡覆蓋的目的，但是只是將虛擬力的合力方向做為調整節點感知方向的依據，每次調整的角度大小不變。調整角度值設定太小，時間步長轉動較小，雖然調整準確度較高，但是推遲了整個網絡穩定狀態的到來;調整角度值設定太大，調整準確度降低，還有可能造成網絡最終不能進入穩定狀態。本文通過建立合力與調整角度大小之間的關系，動態改變節點感知方向的調整量，使整個網絡能夠更快的進入穩定狀態。另外在實際應用中，考慮到成本問題，監測區域中所有的節點都具有移動能力是不現實的，而且也可能由于傳感器節點位置的變化引起部分節點的失效，造成整個網絡的拓撲結構發生變化。因此本文假定所有節點的調整僅限于圍繞一點做旋轉運動，且這一點為節點方向可調到感知模型的頂點。

(1)虛擬力的建立

經過前面的分析，利用虛擬視場解決有向傳感器網絡的區域覆蓋問題可近似等價于質心點與質心點的虛擬斥力作用問題。有向傳感器節點之間存在斥力，并且在2R范圍內，節點之間的距離越近，斥力越大，反之越小。

相鄰傳感器節點vj對vi的虛擬斥力定義為:

俄羅斯國家杜馬信息政策、信息技術和通信委員會副主任亞歷山大·尤先科在人工智能論壇上指出，如今全世界都在競相發展人工智能，在這個領域俄羅斯不能落后，俄羅斯有IT行業優勢，國家對人工智能立法責無旁貸，同時要立法部門和政府部門協同，學術界及社會廣泛支持。

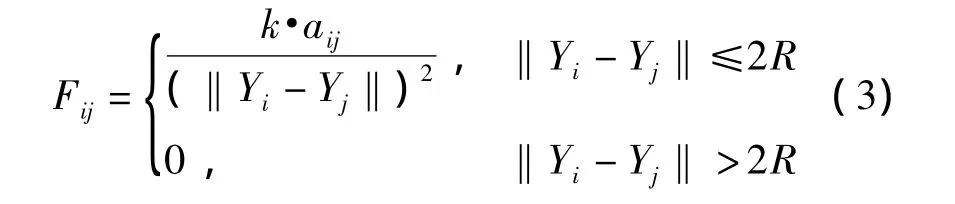
其中，k為斥力常數;aij為單位向量，由節點vj的質心指向節點vi的質心;‖Yi－Yj‖為節點vj與節點vi質心之間的歐氏距離。

(2)合力的計算

定義3有向傳感器網絡中，當節點vj與節點vi質心之間的歐氏距離小于或等于節點感知半徑的2倍時，則互為友鄰節點。

假設節點vi的友鄰節點的集合為Φi，則節點vi質心所受的合力為:Fi=∑j∈ΦiFij，vj∈Φi。由于規定有向傳感器網絡中的節點只能圍繞其感知模型的頂點做旋轉運動，因此節點感知方向的調整只受合力沿切線方向分量F'的影響，如圖2所示。

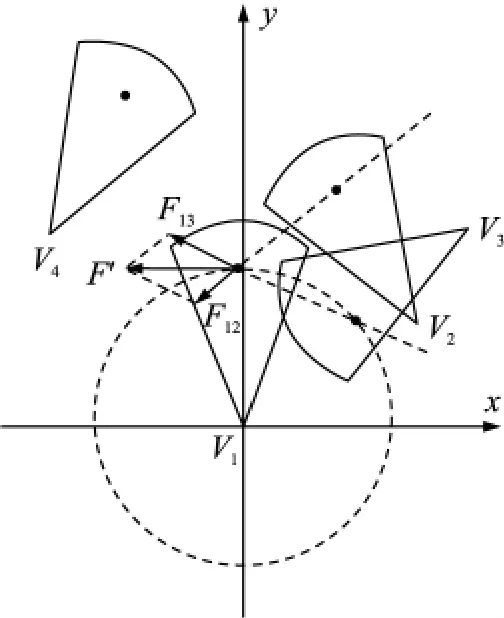
圖2 節點的質心點受力合力分析

2．2 調整角度的計算

從力學的角度講，分量F'和傳感器的質量以及節點做直線運動的加速度有關，但是由于節點只能做旋轉，因此需要將直線加速度轉化為角加速度。則有:

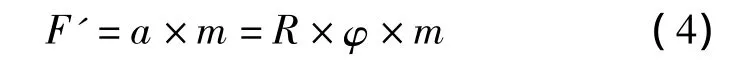
其中:a表示物體的直線加速度，R表示旋轉半徑，φ表示物體的角加速度，m為物體質量。由于調整角度的大小并不受m的影響，因此將式(4)簡化為:

但在本文中，節點并不是一直在做旋轉，而是每做一次旋轉后計算分量F'以及調整角度的值再做旋轉。因此式(5)中角加速度φ可以看作和調整角度有關聯的一個量。

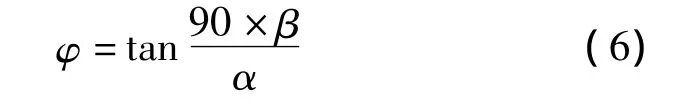
式(6)中α表示節點有效感知角度的一半;β表示節點感知方向的角度調整量。將式(5)與式(6)進行整合，得到:

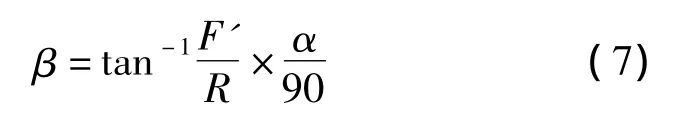
其中，0≤β≤α。

2．3 區域覆蓋增強算法描述

輸入 節點vi及友鄰節點的狀態信息，包括:當前位置、最大感知半徑、感知方向和最大感知角度，角度調整量初始化為0。

輸出 節點vi的最終感知方向。

(1)初始化時間步長計數器t=0;

(2)計算節點vi的方向可調感知模型的質心坐標PVi(t);

(3)計算節點vi友鄰節點集合Φi，X為集合Φi中包含的元素數目;

(4)while(1)

3 算法仿真及分析

通過在Matlab上進行一系列的仿真實驗對本文提出的有向傳感器網絡低冗余覆蓋算法進行驗證。實驗環境及參數取值見表1。

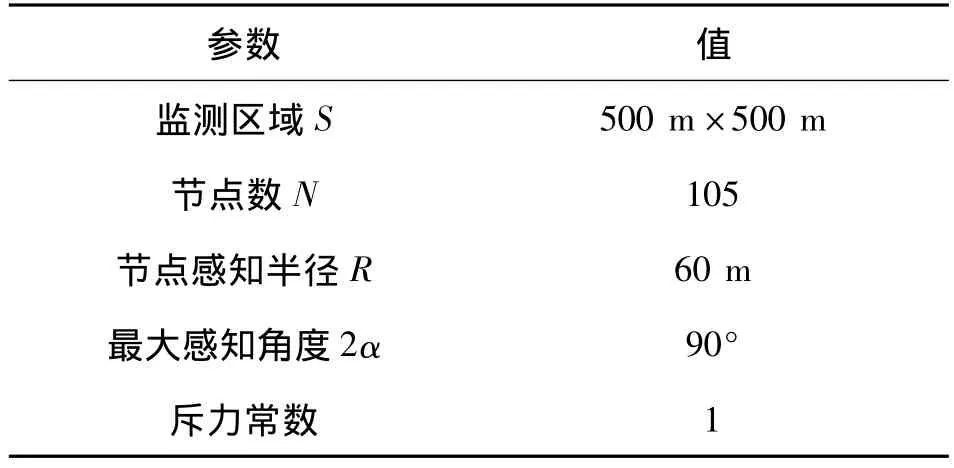
表1 實驗環境及參數取值

按照表1所設定的實驗參數進行實驗，分別記錄每個時間步長網絡的覆蓋率以及網絡中處于激活狀態的節點個數。圖3為網絡中活躍節點個數隨時間變化曲線。圖4顯示了采用PFCEA算法與采用本文算法在初始覆蓋率為65%，其它參數一樣的情況下區域覆蓋性能增強情況。從圖3和圖4可以看出，本文的算法和和PFCEA算法相比，最終的覆蓋增強效果雖然差別不大，但是覆蓋增強的效率卻有明顯的提高，由30個時間步長縮短為25個時間步長，提高了16．7個百分點，同時利用更少的節點達到了同樣令人滿意的覆蓋增強效果。

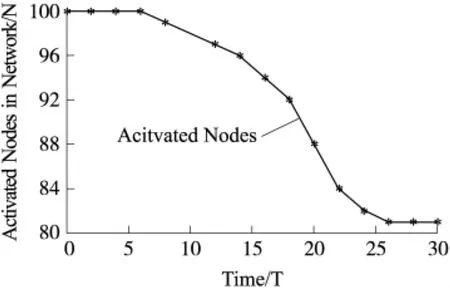
圖3 網絡中活躍結點個數在覆蓋增強過程中的變化曲線

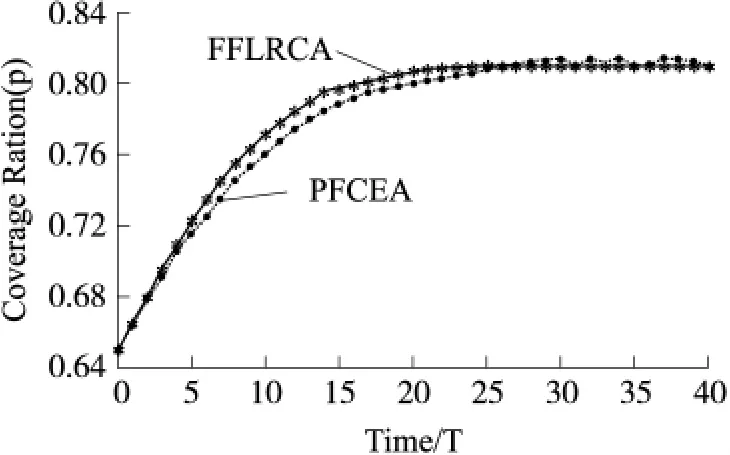
圖4 網絡中活躍結點個數在覆蓋增強過程中的變化曲線

圖5顯示了不同節點規模對FFLRCA算法覆蓋增強效果的影響。可以看出，當R，2α等其它參數一定時，隨著節點規模N的增大，FFLRCA算法對覆蓋率的增強效果增加到一定程度后開始較少。例如N=150時，網絡的初始覆蓋率已經達到了81．94%，相鄰傳感器節點之間形成覆蓋盲區的概率降低，FFLRCA算法的覆蓋增強性能開始消弱。

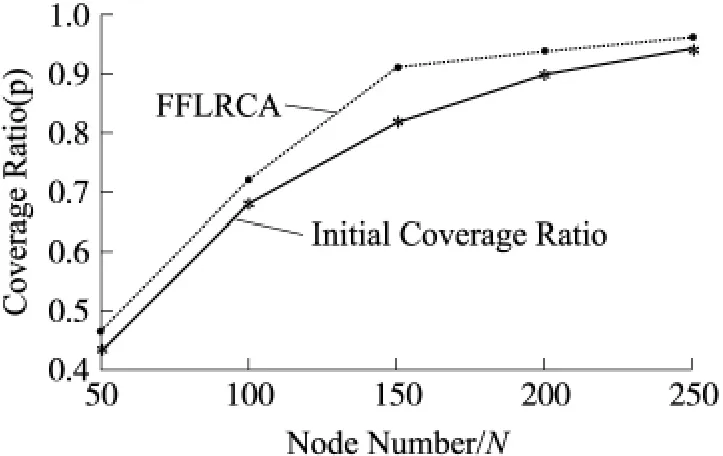
圖5 節點個數N對增強效果的影響，其它參數:R=60，α =45°

圖6顯示了不同節點最大感知角度2α對FFLRCA算法覆蓋增強效果的影響。當節點最大感知角度越小，單個節點的覆蓋區域越小，相鄰節點之間形成重疊區域的可能性就越小，FFLRCA算法的效果就不顯著，隨著節點感知角度的增加，N=110，R=40 m，網絡覆蓋率最高可提升15．1%;隨著節點感知角度的繼續增加，FFLRCA算法帶來的覆蓋增強效果降低。

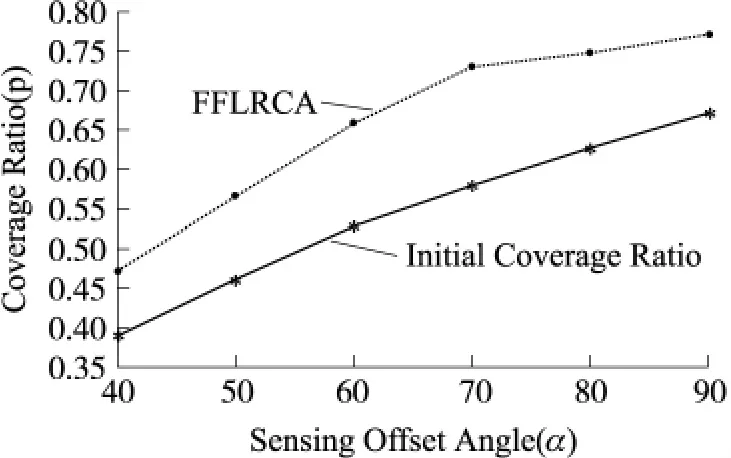
圖6 節點最大感知角度2α對增強效果的影響，其它參數:R=40，N=110

4 結束語

本文主要研究有向傳感器網絡中的區域覆蓋增強問題。在建立改進型的方向可調感知模型后，提出一種基于虛擬力的低冗余覆蓋增強算法。通過引入“虛擬力”以及虛擬力和調整角度之間的關系模型，利用節點之間的斥力逐漸消除網絡中的感知重疊區和盲區，最終實現節點的快速調整和區域的高效覆蓋。本文通過一系列實驗證明了FFLRCA算法的有效性，并詳細的分析了節點規模、最大感知角度對FFLRCA算法增強效果和執行效率提高程度的影響。

[1]Rita Cucchiara．Multimedia Surveillance Systems[C]//Proc of the ACM VSSN2005，New York:ACM Press，2005:1 －10．

[2]Zou Y，Chakrabarty K．Sensor Deployment and Target Localization in Distributed Sensor Networks[J]．ACM Transactions on Embedded Computing Systems，2004，3(1):61 －91．

[3]Ma H D，Liu Y H．On Coverage Problems of Directional Sensor Networks[C]//LNCS 3794:Proc of the Int Conf on Mobile Ad-Hoc and Sensor Networks Berlin:Springer，2005:721 －731．

[4]Tao D，Ma H D，Liu L．Coverage-Enhancing Algorithm for Directional Sensor Networks[C]//Stojmenovic I，Cao JN，eds Proc of the 2nd Int’1 Conf on Mobile Ad-Hoc and Sensor Networks Berlin:Springer-Verlag，2006:256 －267．

[5]Khatib O．Real-Time Obstacle Avoidance for Manipulators and Mobile Robots Research[J]．The International Journal of Robotics Research，1986，5(1):90 －98．

[6]陶丹，馬華東，劉亮．視頻傳感器網絡中路徑覆蓋增強算法研究[J]．電子學報，2008，36(7):1291 －1296．

[7]肖甫，王汝傳，葉曉國，等．基于改進勢場的有向傳感器網絡路徑覆蓋增強算法[J]．計算機研究與發展，2009，46(12):2126－2133．

[8]李石堅，徐從富，吳朝暉，等．面向目標跟蹤的傳感器網絡布局優化及保護策略[J]．電子學報，2006，34(1):71 －76．

[9]Zou Y，Chakrabarty K．Sensor Deployment and Target Localization in Distributed Sensor Networks[J]．ACM Trans on Embedded Computing Systems，2004，3(1):61 －91．

[10]陶丹，馬華東，劉亮．基于虛擬勢場的有向傳感器網絡覆蓋增強算法[J]．軟件學報，2007，18(5):1152 －1163．

[11]溫俊，蔣杰，竇文華．公平的有向傳感器網絡方向優化和節點調度算法[J]．軟件學報，2009，20(3):644 －659．

[12]Habib M Ammari，Sajal K Das．A Study of K-Coverage and Measures of Connectivity in 3D Wireless Sensor Networks[J]．IEEE Transactions on Computers，2010，59(2):243 －256．