基于紅外傳感器和ARM的大氣有害氣體濃度監測系統*

譚韋君，丁萬山

(南京航空航天大學自動化學院，南京210016)

目前我國正處于工業化和城市化發展的加快時期，然而經濟、工業化的迅速發展，帶來了各種工業廢氣排放量的急劇增加和能源的驟減，導致了環境的進一步惡化，嚴重阻礙了社會的可持續發展。其中排放的二氧化碳(CO2)是“溫室效應”的主要來源，二氧化硫(SO2)、一氧化碳(CO)、碳氫化合物(CH4)、硫化氫(H2S)都是對人體有害的氣體，對人體健康有極大危害［1］。因此，研究并設計大氣有害氣體的監測系統對大氣環境的監測具有重要的意義。

近年來國內外許多科研單位對監測大氣有害氣的濃度，開展了一系列的研究，而此類研究多采用接觸式測量方法。由于接觸式傳感器時間分辯率及空間分辯率都有一定的限制，因此國內外很多學者逐漸轉向探索采用光學方法測量氣體的組份濃度。本文介紹了一種運用LED發出的紅外光測量大氣有害氣體濃度的檢測系統，采用特定波長的半導體二極管作為光源，與之相配的光電二極管構成的光電傳感器［4］。系統選用基于ARM7核的S3C44B0作為微處理器，MAX1133作為系統的AD采集模塊，再輔以鍵盤模塊和液晶顯示屏，可脫離PC機獨立完成對有害氣體濃度測量的顯示和控制，另外還可以通過RS485通訊模塊進行遠程傳輸。

1 紅外光譜檢測的基本原理

根據紅外理論，許多化合物分子在紅外波段都具有一定的吸收帶，吸收帶的強弱及所在的波長范圍由分子本身的結構決定［4］。氣體分子的特征吸收帶主要分布在1 μm～25 μm波長范圍的紅外區。這里我們以溫室氣體 CO2為例:CO2在2.7μm、4.3 μm、及11.4μm～20 μm 之間有強吸收帶(圖1)。本系統選擇4.3 μm作為CO2的工作波長，選擇3.6 μm 作為參考波長。

圖1 CO2氣體的吸收帶

對于一定波長的紅外輻射的吸收，其強度與待測組分的關系可以由朗伯特－比爾定理［3］來描述:

式中，I為透射紅外輻射的強度;I0為入射紅外輻射的強度;K為氣體的紅外光吸收系數;C為待測氣體的摩爾百分體積分數;L為紅外輻射穿透過的待測氣體組分的長度。

當紅外輻射穿過待測組分的長度L和入射紅外輻射的強度I0一定時，由于K對某一種特定的待測組分是常數，故透過的紅外輻射強度I僅僅是待測組分摩爾百分濃度的C的單值函數。通過測定透射的紅外輻射強度，就可以確定待測組分的濃度［5］。

2 硬件系統設計

系統由紅外光電傳感器、信號調理電路、16 bit A/D轉換電路和以ARM處理器(S3C44B0)為核心的中央處理單元組成［8］，系統總體框圖如圖2所示。

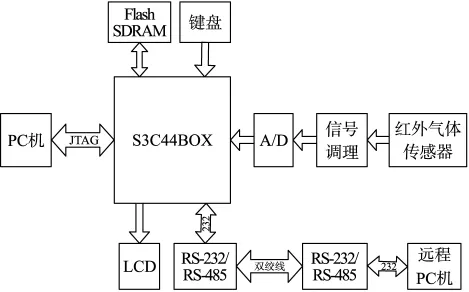
圖2 系統硬件結構框圖

光電傳感器把光強信號轉化為電壓信號，經過信號調理電路進行濾波和放大，然后將得到的電壓信號通過A/D轉換器將模擬量轉化為數字量送入S3C44B0進行數據采集和處理，最后在液晶屏上顯示測量結果，并將測量結果通過RS485通訊模塊發送到遠程PC機上，進行遠程實時的監控。

2.1 傳感器的設計

濃度傳感器的光源LED采用方波來驅動工作，LED采用頻率為10 kHz的方波來進行調制，采用NE555芯片作為振蕩器(圖3)，輸出具有一定周期和占空比的方波，再接MIC2951組成的恒流源電路(圖4)作為LED 的驅動電路［7］。

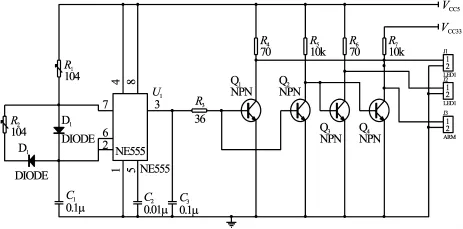
圖3 N555方波驅動電路

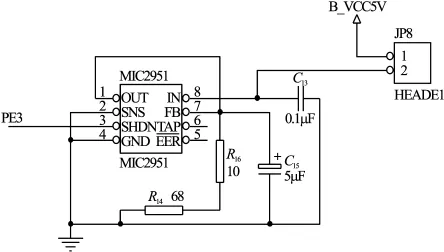
圖4 恒流源電路

同時采用差分吸收法［2－3］中的單光路雙波長技術(圖5)，以消除光源的波動、光電器件的時漂和溫漂等因素帶來的干擾。在兩路相位相反的方波驅動下，光源1和光源2在一個方波周期內輪流發光，其中光源1(LED43)發光波長為4.3 μm，對應 CO2在4.3 μm的吸收峰值，光路中帶有被測氣體吸收后的光強信息;光源2(LED36)發出光波長為3.6 μm，光路中帶有未經被測氣體吸收的光強信息。

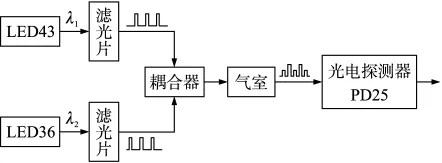
圖5 差分吸收原理圖

探測器(PD25)接收到I1和I2后分別將其轉化為電壓信號V1和V2［6］，經過調理放大電路后，送給ARM中央處理平臺進行數據處理，完成濃度信號的測試。

2.2 A/D轉換模塊

系統選用的A/D轉換器是MAXIM公司的16 bit的MAX1133，MAX1133無須電平轉換就可以直接與 3.3V的 ARM系統相連。MAX1133與S3C44B0的硬件連接如圖6所示。

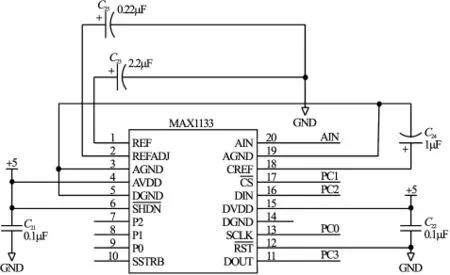
圖6 MAX1133與S3C44B0的硬件連接圖

S3C44B0的PC0口與MAX1133的SCLK連接提供AD轉換器的工作時序;PC1與連接，PC1輸出0選定MAX1133;PC2與DIN連接，提供控制字;PC3在SCLK時序下將A/D轉換結果讀入S3C44B0中。

3 軟件結構

3.1 系統軟件總體流程圖

系統上電后先對整個采集系統進行初始化操作，包括ARM系統的初始化和目標板上外設的初始化，對它們進行參數配置。初始化完成后開始顯示開機畫面，啟動A/D轉換首先要給MAX1133寫入控制字，才能使A/D工作起來，待A/D轉換結束后，要讀取A/D轉換的數據才完成了數據采集這一過程，則S3C44B0對數據進行處理還原為原始濃度信號。根據用戶的按鍵操作，用LCD顯示有害氣體的濃度值或濃度變化曲線，并將數據經串口通過RS485總線發送到遠程監控計算機。系統軟件的流程圖如圖7所示。

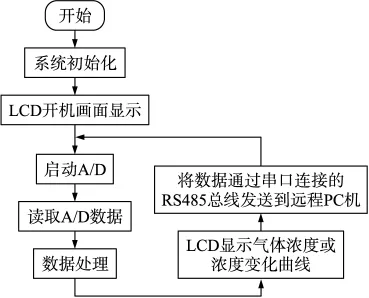
圖7 系統軟件的總體框圖

3.2 數據處理算法［10-11］

粒子濾波適用非高斯噪聲干擾下的非線性系統。采用粒子濾波算法對信號進行去噪處理，提高信噪比。接收到的信號xk受到非線性噪聲的干擾，對動態時變系統建立如下的狀態方程和測量方程:

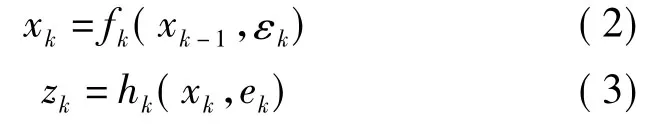
其中，xk是目標在時刻k的狀態向量，εk是過程噪聲，zk是狀態xk的觀測值，ek是觀測噪聲。定義{εk}和{ek}為過程噪聲序列和測量噪聲序列，兩者獨立同分布，且噪聲序列和初始狀態x0彼此相互獨立。

已知k－1時刻目標的后驗概率分布p(xk－1|z1∶k－1)，利用狀態方程(2)得出當前時刻的預測概率分布p(xk|z1∶k－1):

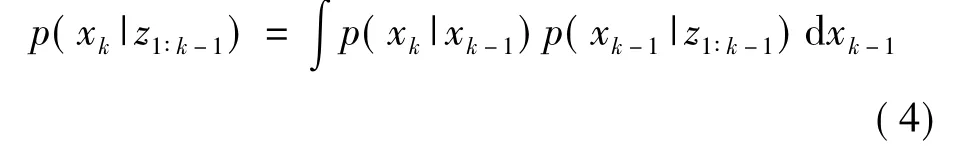
根據貝葉斯更新公式預測概率(3)，得到后驗概率分布 p(xk|z1∶k):

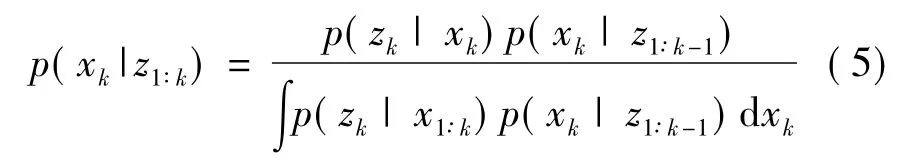
對于非線性、非高斯的動態系統，我們只能尋求遞歸貝葉斯估計的近似最優解。可將后驗概率分布p(xk|z1∶k)可近似表述為:

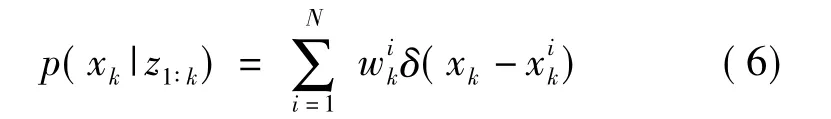
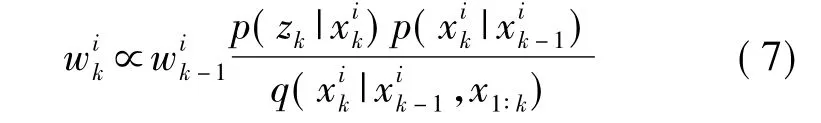
最小均方誤差估計量等價于信號經過重要性權值加權的平均值:

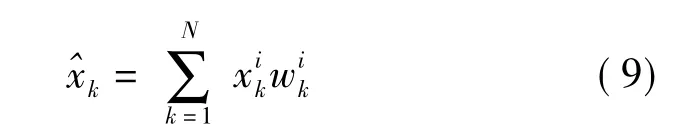
wik表征的是它與粒子與當前時刻真實狀態xk近似程度。在初始分布中抽樣N個初始點……，N);從k－1到k時刻的信號狀態為對應的權值為選取重要函數，通過式(2)產生新的粒子，再通過式(8)更新權值，然后歸一化;最后通過式(9)得出當前時刻的這樣就很好地解決了數據采集與處理中噪聲的干擾，達到了快速、準確地反映采集數據真實值的目的。

4 測試結果

粒子濾波對狀態空間的近似程度只與粒子數N有關，與狀態空間維數的無關，且隨著粒子數N的增加，濾波結果更趨近于真實的信號［9］。在實際的采樣數據濾波過程中，我們取N=200，濾波的結果如圖8所示。

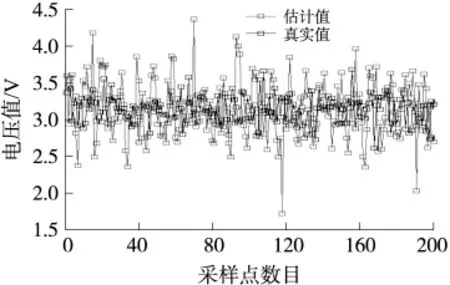
圖8 估計值和真實值比較圖

系統的軟件、硬件分別測試完成后，需要經過系統標定，然后才能用來測試測量。統計CO2體積分數與電壓差值(V0－V)對應關系，建立擬合曲線。假設非線性特性曲線擬合方程［12］的n次多項式為:

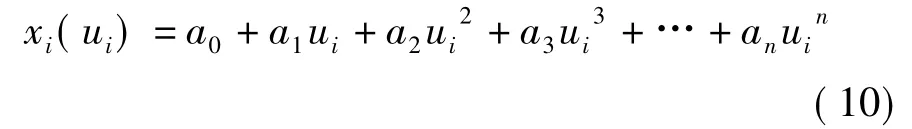
其中，階數n由所要求的精度所確定，本設計中n=6。

對體積分數測試系統進行靜態標定實驗，獲得一組體積分數值和與之對應的輸出值，計算出待定常數a0～a6。將系數a0～a6存入內存，這樣，以后在測試過程中就可以根據式(10)將傳感器的輸出值變換為體積分數值。本測試系統擬合曲線如圖9所示。

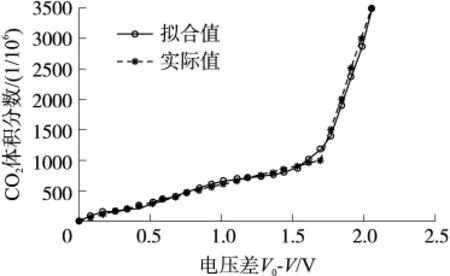
圖9 CO2體積分數與V0－V的擬合曲線

由上圖可知CO2氣體的濃度變化很小，系統具有良好的穩定性和重復性。本系統設備與0.5×10－6的標準測量設備經過實驗比較后，測出系統的測量精度為5×10－6。

5 結束語

應用紅外光譜吸收原理、嵌入式技術和粒子濾波算法設計的大氣有害氣體濃度監測系統，具有靈敏度高、穩定性好，實時性強等特點，且可以實現遠程通訊，可廣泛的應用于工業廢氣、大氣環境等領域的監測和預報。

［1］中國環境保護產業協會環境監測儀器委員會.污染源連續自動監測系統的發展［J］.中國環境產業，2003(4):25－26.

［2］周圍.差分吸收光譜技術在大氣環境監測中的應用研究［J］.河北工業大學學報，2007(11):17－19.

［3］吳希軍，王玉田，田瑞玲，等.取樣光柵濾波的新型光纖甲烷差分檢測系統［J］.傳感器技術學報，2010，23(1):15 －16.

［4］崔厚欣，齊汝賓，張文軍，等.差分吸收光譜法大氣環境質量在線連續監測系統的設計［J］.分析儀器，2008，11(1):7 －12.

［5］丁萬山，孫紅兵.基于激光診斷技術的脈沖爆震發動機多參數自動測試系統［J］.傳感器技術學報，2007，20(9):2060－2062.

［6］Tapia J，Khomenko A V，Cortes-Martinez R.High Accurate Fiber with Two-LED Light Source［J］.Optics Communications.2000，177:219 －223..

［7］Gharavi M.Quantification of Near-IR Tunable Diode Laser Measurements in Flames［C］//2nd Joint Meeting of the U S Sections of the Combustion Institute，USA IEEE March，2001:167 －184.

［8］田澤.嵌入式系統開發與應用［M］.北京:北京航空航天大學出版社，2005(3):28－53.

［9］劉凱.粒子濾波在單通道信號分離中的應用研究［D］.2007(4):38－43.

［10］Michael K Pitt，Neil Shephard.Filtering Via Simulation:Auxiliar Particle Filtering［J］.USA IEEE March，2007:590 －592.

［11］AlexandrosValyrakis，Efthimios E Tsakonas，Nicholas D Sidiropoulos.Stochastic Modeling and Particle Filtering Algorithms for Tracking a Frequency-Hopped Signal［J］.USA IEEE August，2009:3108 －3110.

［12］唐家德.基于MATLAB的非線性曲線擬合［J］.計算機與現代化，2008，5(6):15 －21.