附有高程約束的中國區域定位系統定位精度分析

劉 成,杜曉輝,王 萌

(1.中國科學院國家天文臺,北京100012;2.中國科學院研究生院,北京100190)

0 引 言

2002年,中國科學院的科研人員開始研發有別于GPS類衛星定位系統的、創新的中國區域衛星導航定位系統CAPS[1-3]。CAPS實驗系統使用C波段商用靜止軌道(GEO)通信衛星和小傾角傾斜同步軌道(SIGSO)的通信衛星組成轉發式衛星導航系統,利用通信衛星的轉發功能,將地面原子鐘生成的時間信號和導航電文通過衛星轉發給用戶,實現導航定位。

衛星星座與布局是一個衛星導航系統的重要基礎,在很大程度上決定了系統的定位精度[4-5]。為補充和改善衛星星座的分布,提高用戶的定位精度,CAPS系統創造了應用氣壓測高輔助衛星定位[6]的方法。在氣壓測高技術的輔助下,即使是衛星導航星座全部采用赤道同步軌道(GEO)通信衛星的CAPS-I期工程也實現了三維定位[1,9]。這樣,與發射專用導航衛星的系統相比,建成CAPS系統資金投入較少,具有建設成本低、周期短和性能優越等特點。然而,系統采用的氣壓測高,本身存在著誤差,也會給定位結果帶來誤差。因此,本文從觀測方程的解算方法出發,分析了氣壓測高誤差對CAPS系統定位精度的影響,并通過仿真計算給出了兩者之間的量度關系,從而為氣壓測高技術下的實際定位工作提供了有意義的參考。

1 氣壓測高原理

氣壓測高方法,是利用地球大氣中氣壓隨高度變化的關系,在測量大氣壓的情況下獲得該處的地平高度。用戶接收到CAPS導航電文后,結合實測的氣壓和溫度值,即可求得該點高度值,進入測量方程組進行聯合解算,從而實現三維定位。

重力場內的大氣壓力隨高度增加而減小,通過使用氣壓傳感器來測量氣象參數,即可計算得到精確的相對高度[6-7]。

當大氣處于流體靜力學平衡時,按流體力學原理有:

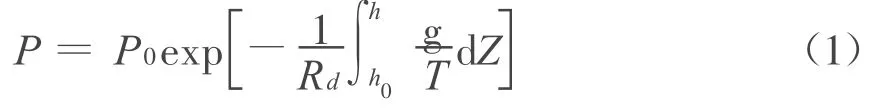
式中:P為用戶所測的大氣壓力;P0為參考點大氣壓;h0為參考點高度;h為用戶設備高度;Rd為氣體參數,取287.05J/(kg?K);T為大氣溫度(K);g為重力加速度。

重力加速度g隨高度變化非常緩慢,常作常數處理。所以上式可化為

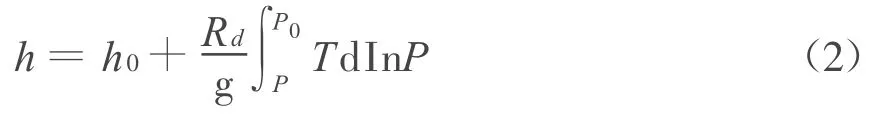
由于大氣溫度隨高度的分布很復雜,難以用函數關系表示,因此,對式(2)直接求積分幾乎是不可能的。為此,通常假設在同樣的氣壓水平上大氣溫度為常數,并取Tm(K)為P0和P之間大氣層中的平均溫度,則有:

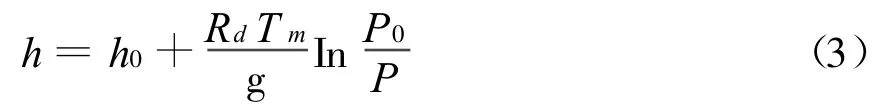
換成以10為底的對數,并用百分度表示溫度后,有:

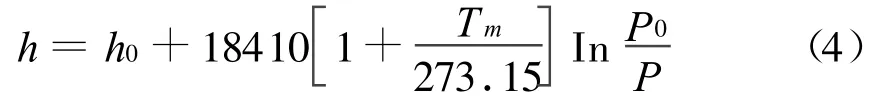
式(4)稱為Laplace壓高方程,即為利用氣壓值測定高度的基本公式。其中,Tm=(T0+TR)/2,T0是基準點溫度,TR是接收機測點測量值[6-8]。

我國境內及周邊,共有1860個氣象站對居地的P0和T0值實行連續監測,CAPS主控站收集和處理氣象站數據,以導航電文方式向用戶廣播。如果用戶位于氣象站附近,則氣象站的h0、P0和T0可直接用于計算用戶設備所在的高度。如果用戶設備離任何一個氣象站均較遠,則可以利用內插法求得h0、P0和T0。

實驗表明:氣象站氣壓高度計工作情況良好時,中國大部分地區高度測量的精度與用戶所處高度有關,如表1[9]所示:

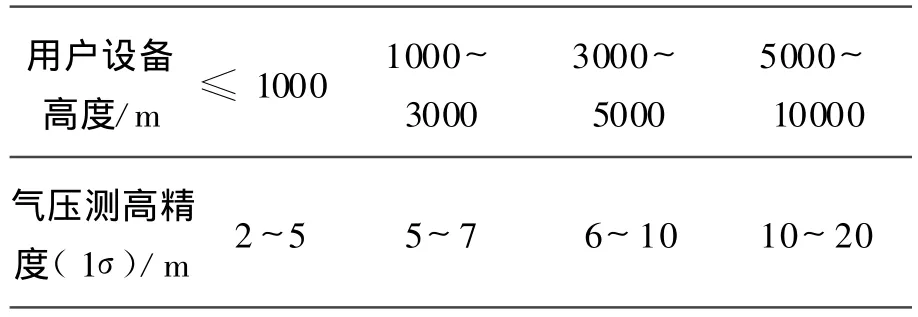
表1 中國大部分地區高度測量精度

2 高程約束觀測方程的解算

CAPS導航定位系統中,氣壓測高技術的效果相當于增設了一個虛擬星座,即相當于一顆衛星處于地球中心點附近,測得的高度值相當于增加了一段偽距值,成為以地心距為半徑的另一個交會球,所以能起到一顆導航衛星的作用[5]。這種情況下的觀測方程為

式中:h為用戶至地球基準橢球的高度;a、b分別為地球基準橢球的長半軸和短半軸。式(5)中的最后一個方程式即為地球橢球約束方程。

求解式(5)的方法有多種[10-11],其中較為有效的一種是,地球橢球方程不直接參與方程組求解,而是單獨列出,僅作為變量之間的約束條件。將式(5)在用戶近似位置(^x,^y,^z)處經線性化,按泰勒級數展開為

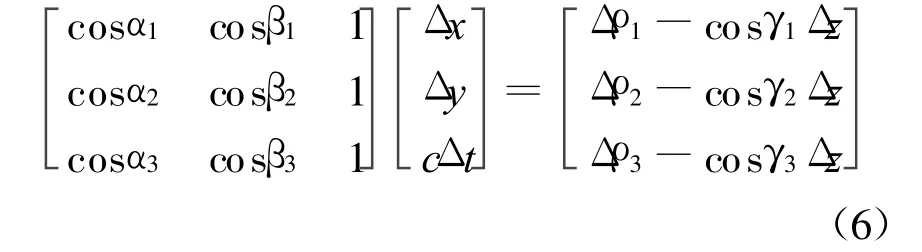
具體求解步驟如下

1)首先可定義初始Δ z=0,將用戶估計位置處的^x和^y代入地球橢球方程,得^z;

2)由式(6),求得 Δ x,Δ y和Δ t;

3)由迭代格式X=^X+Δ X,得用戶坐標x,y和接收機鐘差t;

4)將x和y代入地球橢球方程,得z,并由式Δ z=z-^z計算z坐標增量;

5)重復上述步驟,直至 Δ x、Δ y、Δ z和 Δ t小于某一規定閾值[10-12]時,迭代終止。

3 仿真與分析

中國區域定位系統CAPS-I中,四顆衛星的位置坐標 Si,j(X,Y,Z)用地心地固直角坐標系(ECEF)給出(單位:m),衛星具體信息如表2所示。

表2 中國區域定位系統CAPS-I衛星信息

衛星C、D在傾斜軌道上的相位差約為120°(即過赤道的時間差約為8 h),仿真中取GM=3.986005e14;地球自轉角速度ω=7.2921151467e-5 rad/sec;WGS-84橢球長半軸a=6378137 m;偏心率e=0.081819190842622。

記等效偽距測量均方根誤差為σρ,氣高測高均方根誤差為σh,三維坐標位置定位均方根誤差為σu。仿真計算時,針對10種不同的衛星空間分布情況,在每一種空間分布的偽距值上加上均方根為特定值的隨機誤差(設定為2 m,即σρ=2 m),生成多組、大樣本的誤差分布數據。

3.1 觀測衛星數目為四顆

3.1.1 高程約束算法定位結果

首先考察高程約束算法的定位解算誤差。在仿真中,設定氣壓測高的均方根誤差為σh=2 m,利用上述高程約束解算方法進行100組絕對單點定位解算,并將定位誤差結果與經典球面交會解算方法相比較,如圖1所示。

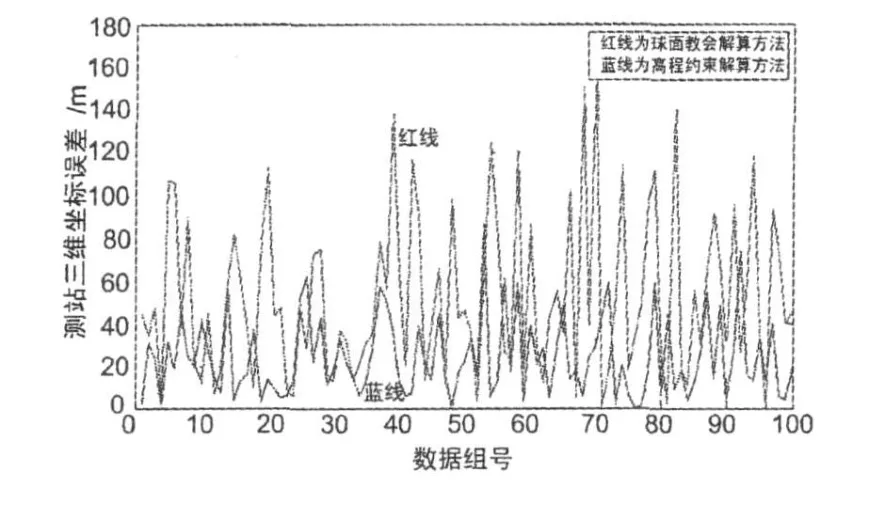
圖1 四顆衛星時高程約束算法定位結果示意圖

從圖1中可以看出,高程約束算法明顯地改善了原球面交會解法的定位精度。統計圖1中的數據可知:原球面交會解算方法三維定位誤差為1σ=65.3 m,高程約束算法三維定位誤差為1σ=33.1 m。高程約束算法把原定位解算誤差減小了約50%。

3.1.2 氣壓測高誤差對定位結果的影響

實際定位工作中,由于用戶儀器設備精度和所處位置海拔高度不同等原因,測量得到的氣壓測高誤差σh也會不盡相同。為此,在仿真計算中令σh為各種不同的值(0～20 m),依次進行高程約束定位解算,并統計出每個σh值所對應的定位誤差均方根值σu,以分析氣壓測高誤差對最終定位結果的影響。如圖2所示。

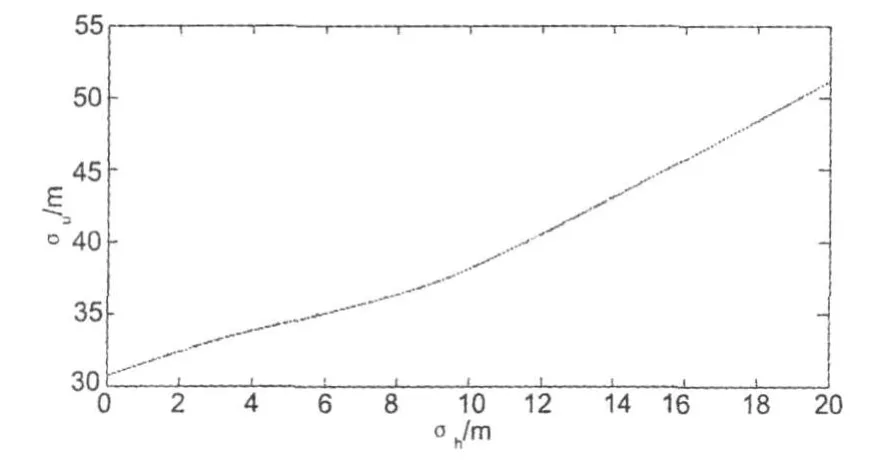
圖2 四顆衛星時高程誤差與定位解算結果關系示意圖

從圖2中可以看出,σh與σu呈現出大致的線性關系。

這個結論說明,氣壓測高誤差σh和由它所產生的那部分定位誤差的量值是基本相同的,并不會放大最終的坐標位置誤差。為建立誤差模型,可以利用樣條插值方法,對圖中的曲線進行一次曲線擬合,得到氣壓測高誤差與定位誤差的關系式。一次曲線擬合的表達式可以寫為

式中:定義σh0為σh=0 m時的三維定位誤差;μ為σh與σu之間的量度關系系數。在本情況下,σh0=30.70 m,μ=1.005。σh與σu之間的關系可表達為

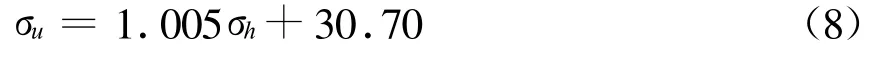
式(8)即為用戶能夠觀測到A、B、C、D四顆衛星時,氣壓測高誤差對CAPS系統定位精度影響的近似計算表達式。在與本仿真情況相近的實際工作中進行綜合定位誤差分析時,μ即可以近似地取為1。

分別統計各坐標方向上的誤差分量大小,結果如圖3所示。

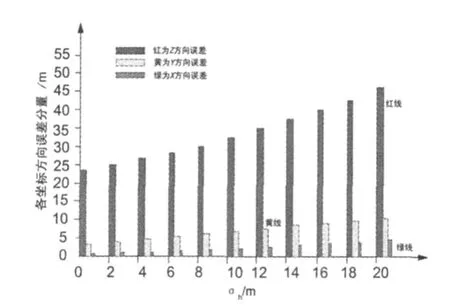
圖3 四顆衛星(σρ=2 m)時各坐標方向上的誤差分量

從圖3中可以看出,在σh逐步增大的過程中,氣壓測高誤差對定位精度所帶來的影響,在Z坐標方向上最大、X坐標方向上最小。

3.2 觀測衛星數目為三顆

3.2.1 高程約束算法定位結果

當用戶只能觀測到上述四顆CAPS衛星中的三顆時,原本無法進行三維定位工作;但在氣壓測高技術的輔助下,起到了一顆虛擬衛星的作用,從而可以實現三維定位。只是星座DOP值較大,定位誤差也會較大。此時,高程約束算法絕對單點定位結果如圖4所示。

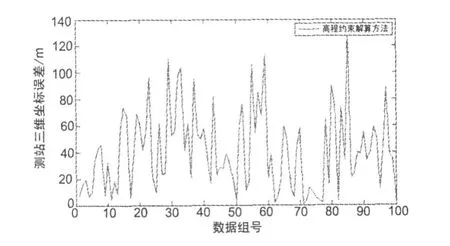
圖4 三顆衛星時高程約束算法定位結果示意圖

統計圖1中的數據可知,此時高程約束算法三維位置定位誤差約為1σ=53.6 m。

3.2.2 氣壓測高誤差對定位結果的影響

三顆觀測衛星的情況下,同樣在仿真計算中令σh為各種不同的值(0～20 m),依次進行高程約束定位解算,并統計出每個σh值所對應的定位誤差均方根值σu,如圖5所示。

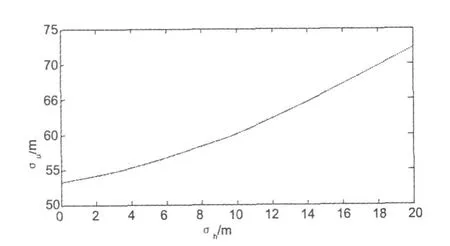
圖5 三顆衛星時高程誤差與定位解算結果關系示意圖

同樣,通過一次樣條插值可以得到參數 μ=0.953。此時,σu與σh之間滿足下列誤差模型:

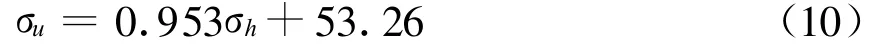
式(10)即為用戶能夠觀測到A、B、C、D四顆衛星中的三顆時,氣壓測高誤差對CAPS系統定位精度影響的近似計算表達式。

從圖4、圖5可以看到,即使在只有三顆觀測衛星的情況下,CAPS-I也能通過氣壓測高的輔助作用順利實現三維定位。分別統計各坐標方向上的誤差分量大小,結果如圖6所示。

可以看出,在σh逐步增大的過程中,氣壓測高誤差對定位精度的所帶來的影響,依然是在Z坐標方向上最大、X坐標方向上最小。

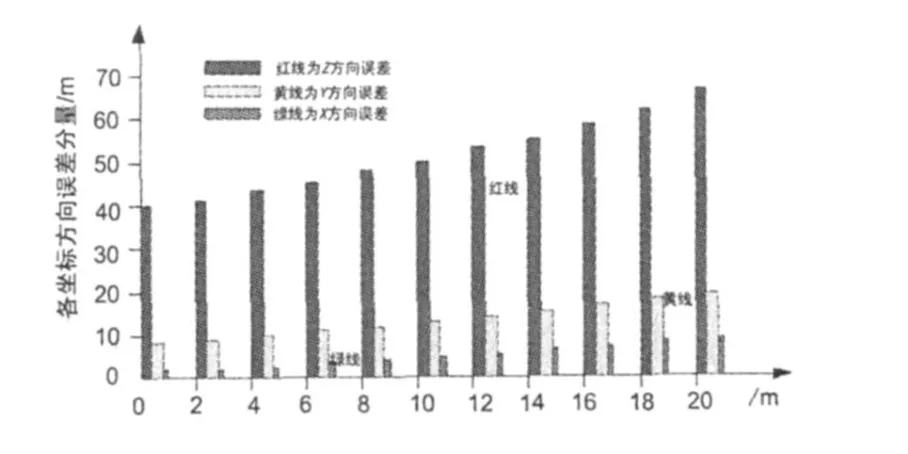
圖6 三顆衛星(σρ=2 m)時各坐標方向上的誤差分量

從以上各種情況下的仿真結果可知,無論觀測衛星的數目是三顆還是四顆,也無論偽距測量值的誤差大小是多少,氣壓測高誤差總與三維位置定位誤差成近似的一次線性關系,且兩者之間的線性系數可以近似取1。換言之,氣壓測高誤差和由它所產生的那部分定位誤差的大小是基本相同的,并不對定位誤差產生額外的放大作用。仿真計算中每種情況下的統計均為大樣本數據統計,所以各統計結果具有可靠的統計特性。

4 結 論

通過仿真計算與統計分析,我們可以得到以下若干結論:

1)無論觀測衛星數目為三顆還是四顆,即使PDOP值較差,在氣壓測高的約束和輔助作用下,CAPS-I系統也都能順利地獲得測站三維位置定位結果,并且能夠將誤差控制在一定范圍之內。未來,隨著CAPS系統衛星星座的逐步完善與發展,相信會得到更好的定位結果。

2)無論觀測衛星的數目為幾顆,也無論偽距測量值的誤差大小是多少,氣壓測高自身誤差對定位精度的影響總是比較獨立的,與三維位置定位誤差成近似的一次線性關系,且兩者之間的線性系數可以近似取為1。也就是說,氣壓測高誤差和由它所產生的那部分定位誤差的量值是基本相同的,并不會對最終的坐標位置誤差起放大作用。

3)氣壓測高本身誤差對定位結果的影響,大部分體現在Z方向上。

4)在實際工作中,我們可以根據不同的衛星星座及氣壓測高情況,統計和建立如上文所述的先驗誤差模型及公式,從而可以指導CAPS等衛星系統對氣壓測高約束下的定位結果進行適當的改正和精化。

[1] Ai G X,Shi H L,Wu H T,et al.Positioning system based satellite communication and Chinese Area Positioning System(CAPS)[J].Chin J Astron Astrophys,2008,8(6):611-635.

[2] 艾國祥,施滸立,吳海濤,等.轉發器衛星通信導航定位系統,中國:200410046064.1[P].2004-06-06.

[3] 施滸立,孫希延,李志剛.轉發式衛星導航原理[M].北京:科學出版社,2009.

[4] Kaplan E D.Understanding GPS principlesand applications[M].Artech House London,UK.,1996.

[5] 周忠謨,易杰軍,周 琪.GPS衛星測量原理與應用[M].北京:測繪出版社,2004.

[6] 艾國祥,盛裴軒,杜金林,等.應用于CAPS的氣壓測高虛擬衛星[J].中國科學G輯:物理學?力學?天文學,2008,38(12):1702-1710.

[7] 盛裴軒,毛節奏,李建國,等.大氣物理學[M].北京:北京大學出版社,2003:30-35.

[8] United States committee on Extansion to the Standard Atmosphere.U.S.Standard Atmosphere[M].Washington:US Government Printing Office,1976.

[9] 艾國祥,施滸立,吳海濤,等.基于通信衛星的定位系統原理[J].中國科學G輯:物理學?力學?天文學,2008,38(12):1615-1633.

[10] 施滸立,裴 軍.轉發式衛星導航定位系統量測方程解[J].中國科學G輯:物理學?力學?天文學,2008,38(12):1687-1701.

[11] 施滸立,劉 成,耿建平,等.地球高程作為約束時的衛星定位觀測方程求解方法的探討[G].CAPS內部資料,2010.

[12] 紀元法,孫希延.中國區域定位系統的定位精度分析[J].中國科學G輯:物理學?力學?天文學,2008,38(12):1812-1817.

[13] 施滸立,艾國祥,韓延本,等.退役衛星的多生命周期利用[J].中國科學G輯:物理學?力學?天文學,2008,38(12):1731-1737.