變剛度楔形體板架落體砰擊試驗研究

莫立新，王 輝，蔣彩霞，徐 春

（1大連理工大學船舶工程學院，遼寧 大連 116024；2中國船舶科學研究中心，江蘇 無錫 214082）

1 引 言

船舶在海上大浪中高速航行時，不可避免地會發(fā)生船體與波浪的劇烈砰擊現(xiàn)象。根據波浪沖擊位置的不同，一般有艏外飄砰擊、艏艉底砰擊、舷側平臺砰擊以及多體船的濕甲板砰擊等[1]。強烈的砰擊作用會導致船體局部結構的破壞甚至主船體強度的喪失。目前，砰擊問題越來越引起人們的關注，ISSC從2006年開始成立了專門的脈沖載荷委員會進行研究[2]。由于砰擊是一種船體與波浪相互作用的復雜水動力現(xiàn)象，砰擊壓力具有局部性、瞬時性及快速移動性等特點，對砰擊現(xiàn)象的研究具有相當的難度，研究手段包括理論分析、數值計算和試驗等[3]。考慮到砰擊壓力的作用特點，如何將砰擊壓力峰值轉化為結構設計和校核需要的等價均布靜壓力是船體局部結構設計中最為關心的問題。對這個“折減系數”的問題，很多研究者已經做了相應的研究工作[3-9]。就目前的研究水平來看，模型試驗仍然是最準確和最經濟的一種手段。本文通過對四種剛度楔形體板架進行水池中的落體沖擊試驗研究，就設計者關心的折減系數問題，重點研究剛度的變化對折減系數的影響，并對船體局部結構設計給出一些有益的建議。模型試驗的結果還可作為理論預報及數值計算比較分析的依據。

2 試驗描述

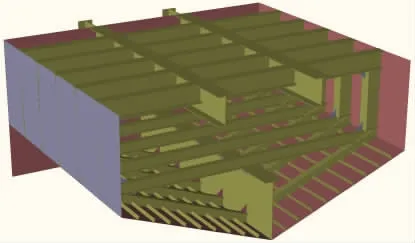
圖1 試驗模型三維視圖Fig.1 3D view of the test model

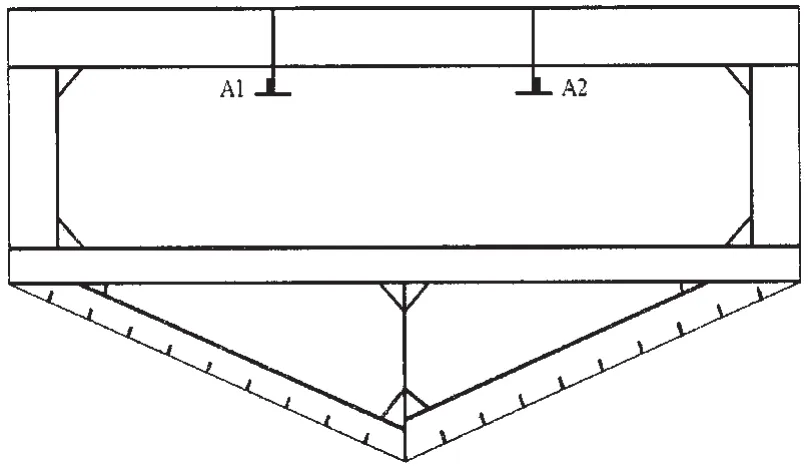
圖2 試驗模型二維剖面圖Fig.2 2D section view of the test model

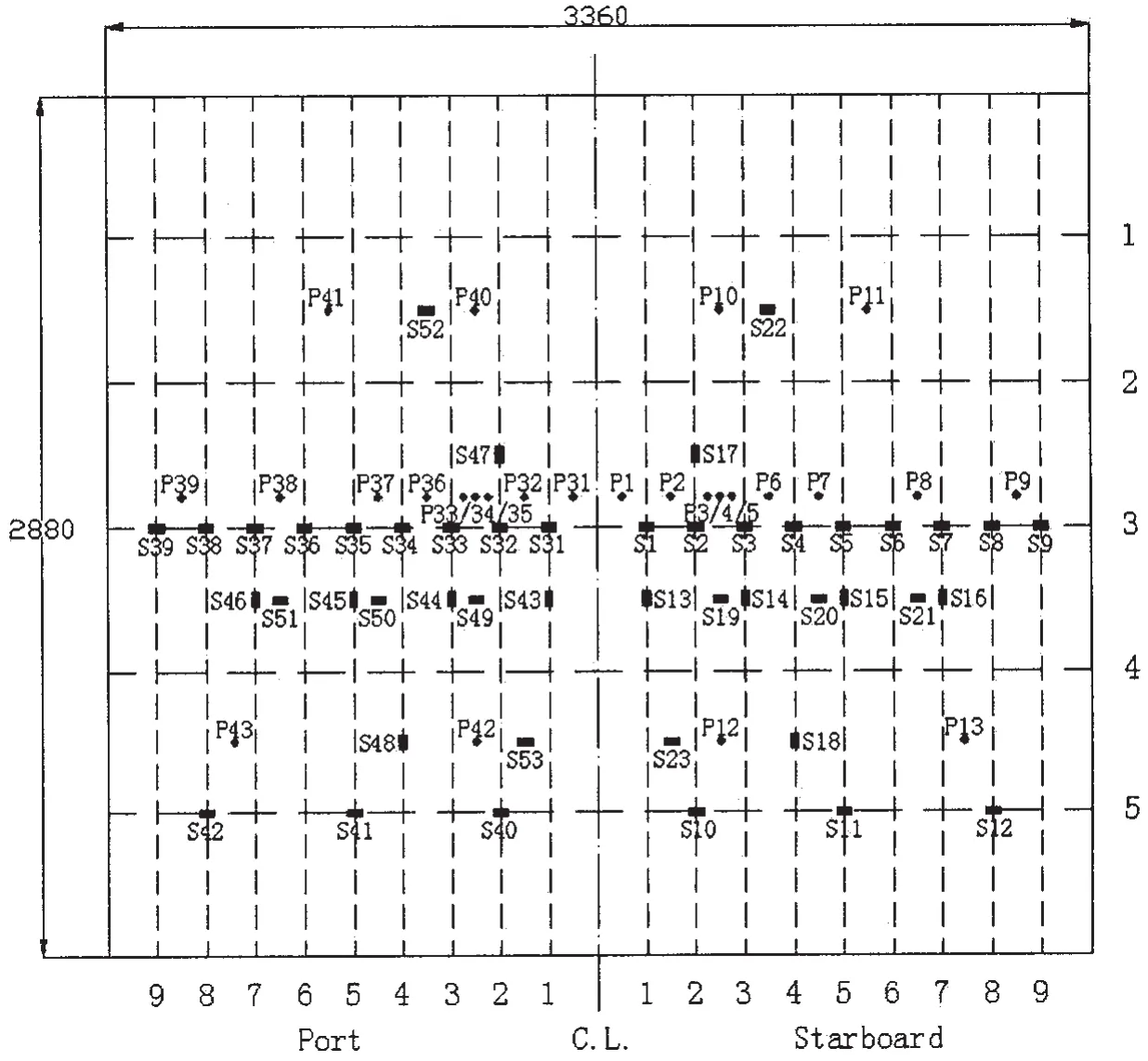
圖3 試驗模型結構特征與測點分布Fig.3 Structure characteristics and measuring points

模型試驗的研究對象為由四組彈性板架組成兩個楔形體模型，即模型一（由板架1和板架2組成）和模型二（由板架3和板架4組成）。考慮到設計模型的自重遠大于板架的結構重量，落體砰擊瞬間持續(xù)時間很短，左右兩邊彈性差別對楔形體模型運動的影響可忽略不計，這樣的設計可一次實施兩種剛度的楔形體板架落體砰擊試驗，并減少了試驗的不確定性和節(jié)約成本。每個模型左右板架四周邊界條件都被設計為加強結構（剛性邊界條件），以減少板架間的相互影響。

模型被設計為二維形式，模型的外形及結構形式在長度方向上均保持不變。為了盡可能使模型在自由落體入水沖擊過程中的流體呈二維流動，模型前后端的艙壁在下方作了適當的加寬和延伸。為了使模型在底部入水后具有較大的浮力儲備，楔形體板架舷側頂部增加了直壁式干舷。模型采用普通鋼材料建造，主尺度為2.88m（長）×3.36m（寬）×1.645m（高），楔形體底部斜升角為21°。四種剛度板架的結構尺寸見表1，模型一和模型二的重量分別為3.5t和3.25t。兩個試驗模型的三維視圖及二維剖面圖見圖1和圖2，模型內部的結構形式俯視見圖3。

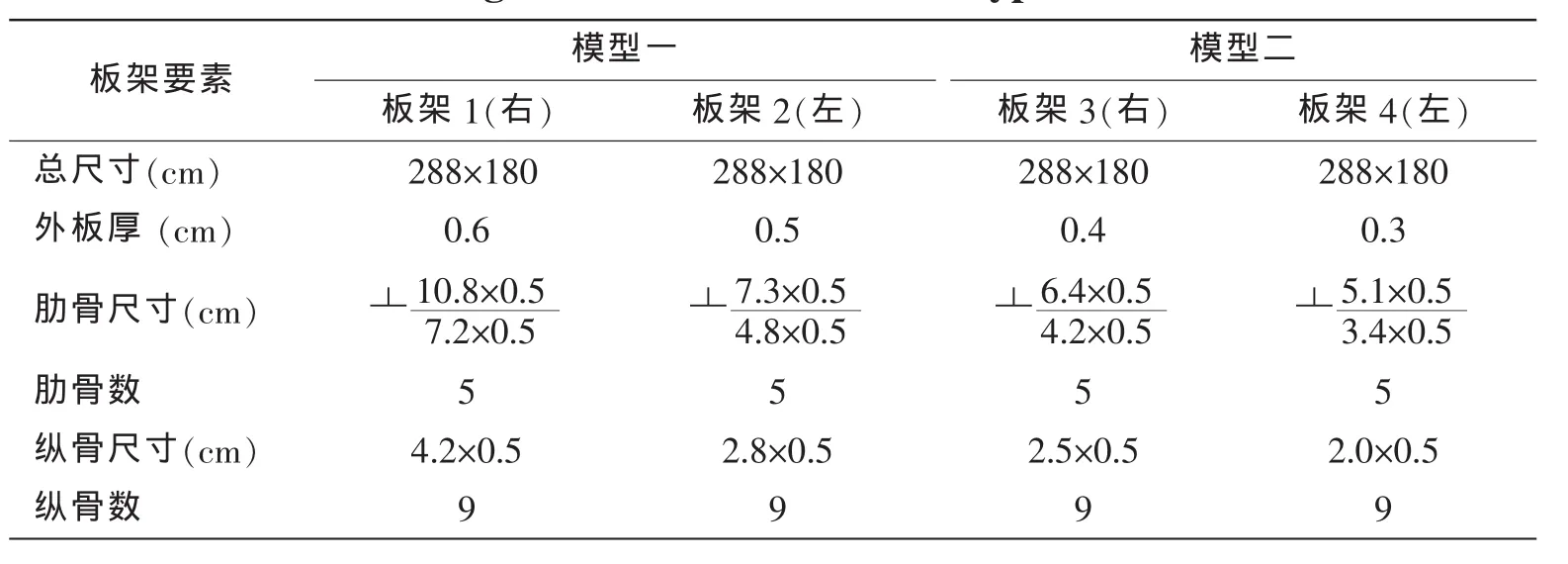
表1 四種剛度板架的結構尺寸Tab.1 Grillage member size with four types of stiffeness

在每組板架的板格上布置了13個壓力測點（以P為首字母）；在肋骨、縱骨、板格上布置了23個應力測點（以S為首字母）；在模型上部兩根強中縱桁上左右對稱布置兩個加速度測點（以A為首字母），測點見圖2和圖3。

測量信號的采樣頻率為10kHz，加速度信號經積分后可以得到模型下落速度的變化曲線。模型工況設計遵循流體動力相似原則，并根據實船可能達到的入水砰擊速度確定模型自由落體高度。考慮到砰擊壓力的離散性，每個高度都進行了數次重復試驗。模型試驗的下落高度和次數見表2。

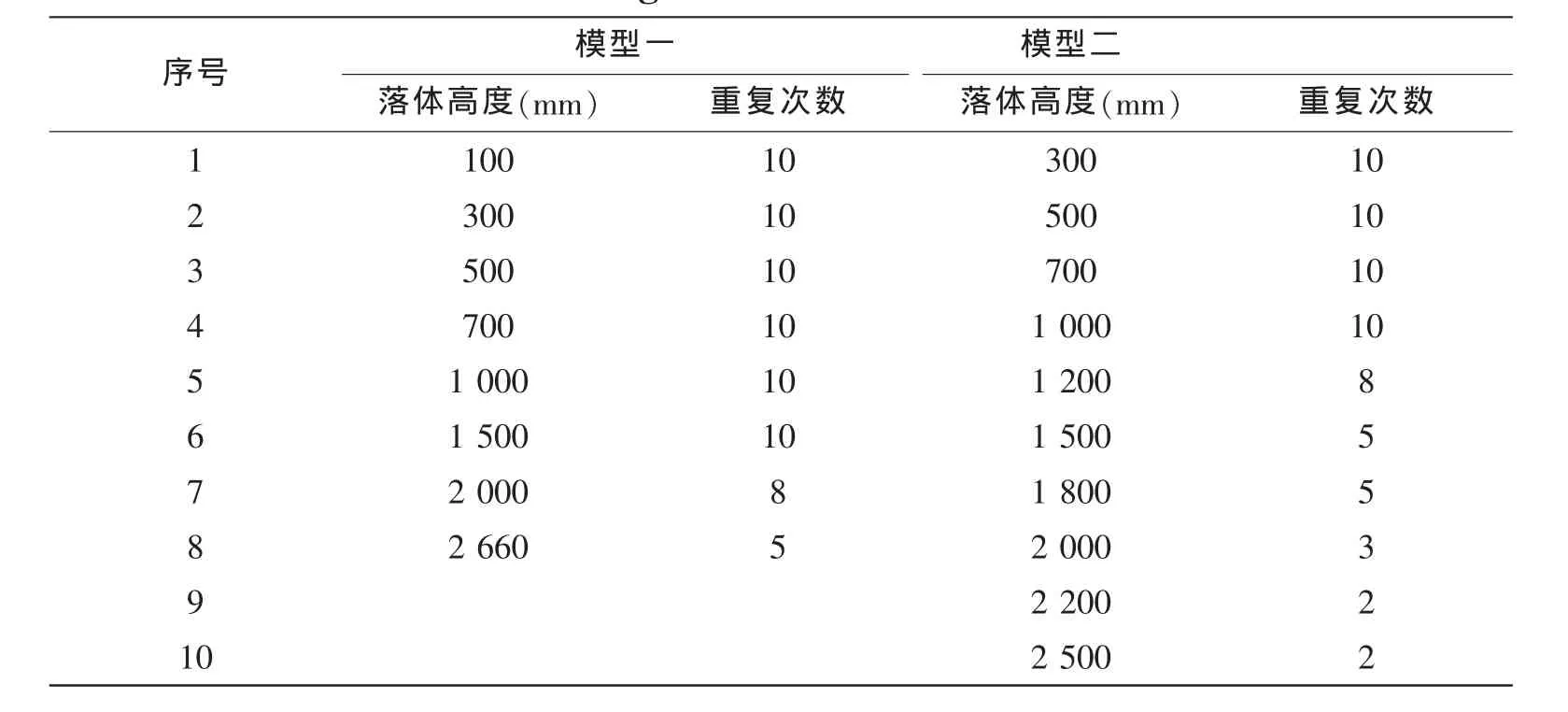
表2 模型試驗落體高度和次數Tab.2 Heights and times of the tests

3 結果分析

兩個模型自由落體過程中，在彈性范圍內，四個板架響應特征基本一致。這里，以板架4為例，模型的落體砰擊過程見圖4，入水砰擊過程中剖面四個典型壓力點的響應曲線見圖5，四個典型肋骨應力測點的響應曲線見圖6，另外，由加速度曲線積分得到的模型落體速度曲線見圖7。

圖4 模型的落體砰擊過程Fig.4 Dropping of the test model

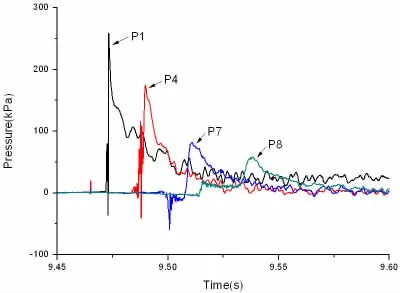
圖5 楔形體板架砰擊壓力分布（板架4，H=1 500mm）Fig.5 Distribution of the slamming pressure(Grillage 4,H=1 500mm)

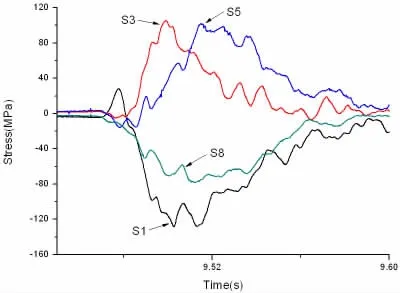
圖6 肋骨框架應力分布（板架4，H=1 500mm）Fig.6 Distribution of the frame stress(Grillage 4,H=1 500mm)

由圖5和圖6可知，楔形體板架上沿肋骨方向各點砰擊壓力依次出現(xiàn)峰值，隨著入水砰擊速度的大幅減小，砰擊壓力峰值也成倍減小。就板架4在1 500mm高度工況而言，最大砰擊壓力出現(xiàn)在楔形體尖點附近的P1點，達到260kPa；而在接近舷側處的P8砰擊壓力峰值只有59kPa。另外，砰擊壓力的脈沖寬度也隨著砰擊速度的減小而增大，就板架4在1 500mm高度工況而言，P1點壓力脈沖寬度在10ms左右，而P8點則達到了28ms。對于板架中部的P4和P7點，砰擊壓力脈沖在上升之前出現(xiàn)了短暫的負壓振蕩，這很可能是由于板架振蕩導致壓力傳感器的物理反應，而非真實的壓力脈沖。

由圖6可知，接近楔形體尖點的肋骨應力測點S1首先出現(xiàn)一個拉應力，然后迅速轉變?yōu)閴簯Γ拷蟼鹊睦吖菓y點S8則一直在壓應力狀態(tài)；S1的應力峰值要大于S8的應力峰值，但在砰擊后半程非常接近。這說明肋骨框架兩邊為剛度很大的彈性固定端邊界條件，S1一端的彈性系數要稍大于S8一端。肋骨框架中間位置的S3和S5隨著砰擊壓力峰值的移動依次出現(xiàn)應力峰值，最大峰值差幾乎一致。整個板架的應力時域分布說明肋骨框架兩端為接近剛性固定邊界，上下部分的應力差別只是由于砰擊壓力峰值空間的移動和量值的變化造成的。

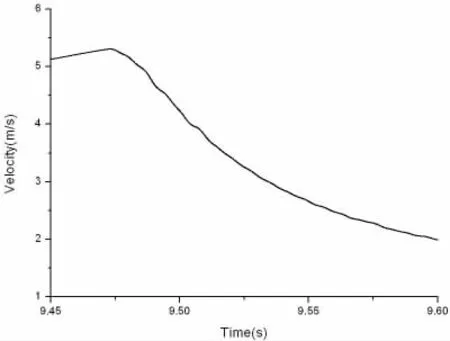
圖7 楔形體落體速度曲線（板架4，H=1 500mm）Fig.7 Dropping velocity of the wedge(Grillage 4,H=1 500mm)

模型二在1 500mm高度的壓力和應力測點共五次落體試驗測量數據按測點分布見圖8。可以看到，在此落體高度下，除少數壓力測點出現(xiàn)隨機性跳躍以外，大多數測點重復性良好，證明了試驗測試系統(tǒng)和測量數據的有效性。通過對壓力和應力數據整理和分析，可對試驗模型板架的折減系數進行有效的分析。

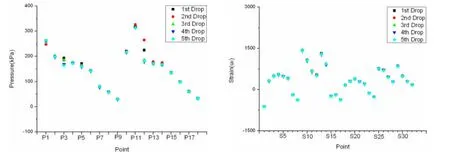
圖8 壓力和應力測點在典型落體高度下的重復測量數據（模型二，H=1 500mm）Fig.8 The repeated measured pressure and stress on one typical height(Model 2,H=1 500mm)

4 折減系數分析

根據文獻[3，8-9]，如果在一定的邊界條件下，因砰擊壓力的沖擊作用引起的構件中的動應力的最大值與作用于該構件上的均布靜壓力下的靜應力最大值相當的話，則可以定義該均布靜壓力為等價均布靜壓力Peq（Equivalent static pressure），它與構件上各點砰擊壓力峰值的平均值的比值為砰擊壓力的折減系數 Kr（Reduction factor），即

Kr的量值不僅反映了砰擊壓力的不均勻程度，也體現(xiàn)了砰擊過程中構件的動荷效應，以及流體與結構之間的耦合影響。一旦掌握了作用在結構物上的砰擊壓力峰值及其平均值，只要乘上該折減系數，就可以得到結構在砰擊壓力作用下的等價均布靜壓力Peq，這樣結構的強度評估就可采用靜力強度計算方法進行。因此，如何獲得折減系數Kr，就成為在砰擊載荷作用下局部結構強度理性設計的一個關鍵。

式中β單位為（°）。上式可適用于3°≤β≤45°，且Kn≤1。可見Kn僅與楔形體的斜升角β有關。

由于本次試驗模型為典型的板架結構且具有簡單的邊界條件，這里采用成熟的結構力學公式對整個板架在均布壓力作用下肋骨框架的應力響應作計算分析。根據模型結構的布置，這里對試驗板架的四周假定為剛性固定邊界條件。

根據交叉梁系的概念，由于試驗楔形體板架的肋骨剛度要遠強于縱骨，則可以把由一根交叉梁（肋骨）和很多同樣的主向梁（縱骨）組成的板架彎曲問題歸結為連續(xù)彈性基礎上的交叉梁彎曲問題。可以認為，在主向梁的數目很多時，作用在板架上的分布外載荷直接由主向梁承受，而交叉梁僅承受在節(jié)點處的相互作用的反力R，這些反力可以用沿某個交叉梁長度分布的載荷r來代替。

這樣交叉梁的彎曲方程寫為

由在節(jié)點處的主向梁撓度ω的表達式

可將交叉梁的彎曲方程寫為

以上方程式描述了在強度為q的分布載荷作用下，剛度為k的彈性基礎交叉梁的彎曲。

引入無量綱參數u，表征確定彈性基礎梁彎曲要素的表函數自變量，u按下式求得

而受均布載荷q作用下的彈性基礎梁的撓度公式為：

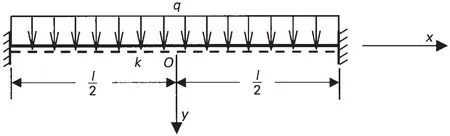
圖9 彈性基礎梁計算模型Fig.9 Theoretical model of elastic based beam

因此可將計算模型轉化為兩端剛性固定受均布載荷作用的彈性基礎梁，見圖9。

由于此梁的載荷與結構對稱于跨度中點，故坐標原點取跨度中點。這樣在x=0處θ0=0，N0=0，代入均布載荷彈性基礎梁的撓曲線方程，可以得到梁的撓曲線方程如下：

從而可以求得梁的彎矩方程為

特別地，梁中點及端點的彎矩可算出如下：

彈性基礎梁翼板上的應力可以由以下公式求得：

其中yd為翼板距彈性基礎梁中和軸的距離。

由以上分析并根據結構力學公式，可得到試驗板架各個參數的取值及梁中點翼板上的最大應力與單位載荷之間的關系見表3。

這樣，對三個落體高度下，試驗模型四個板架的砰擊壓力及折減系數的分析見表4。根據對比可知：

（1）對于不同結構，砰擊壓力折減系數各不相同。對于剛度較弱結構，由于彈性影響，砰擊壓力可能會降低，而結構的響應會增大，砰擊壓力折減系數則會相應地增大，這是結構設計中必須注意的問題。

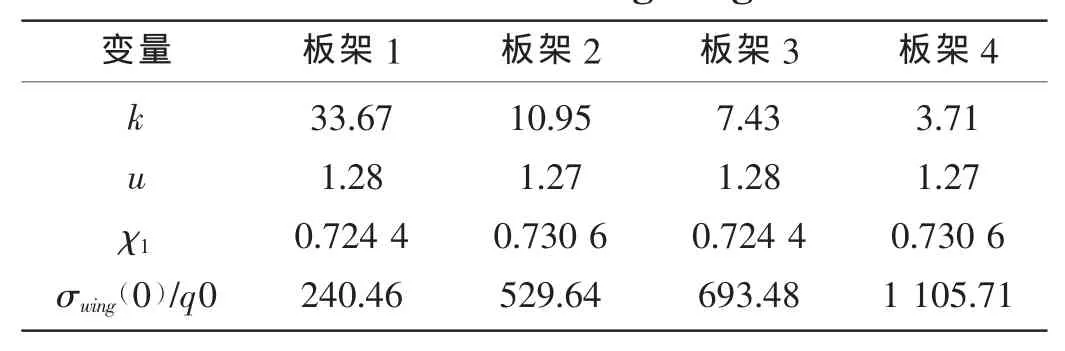
表3 試驗板架計算模型參數與計算結果Tab.3 Theoretical model coefficients and results of the test grillages

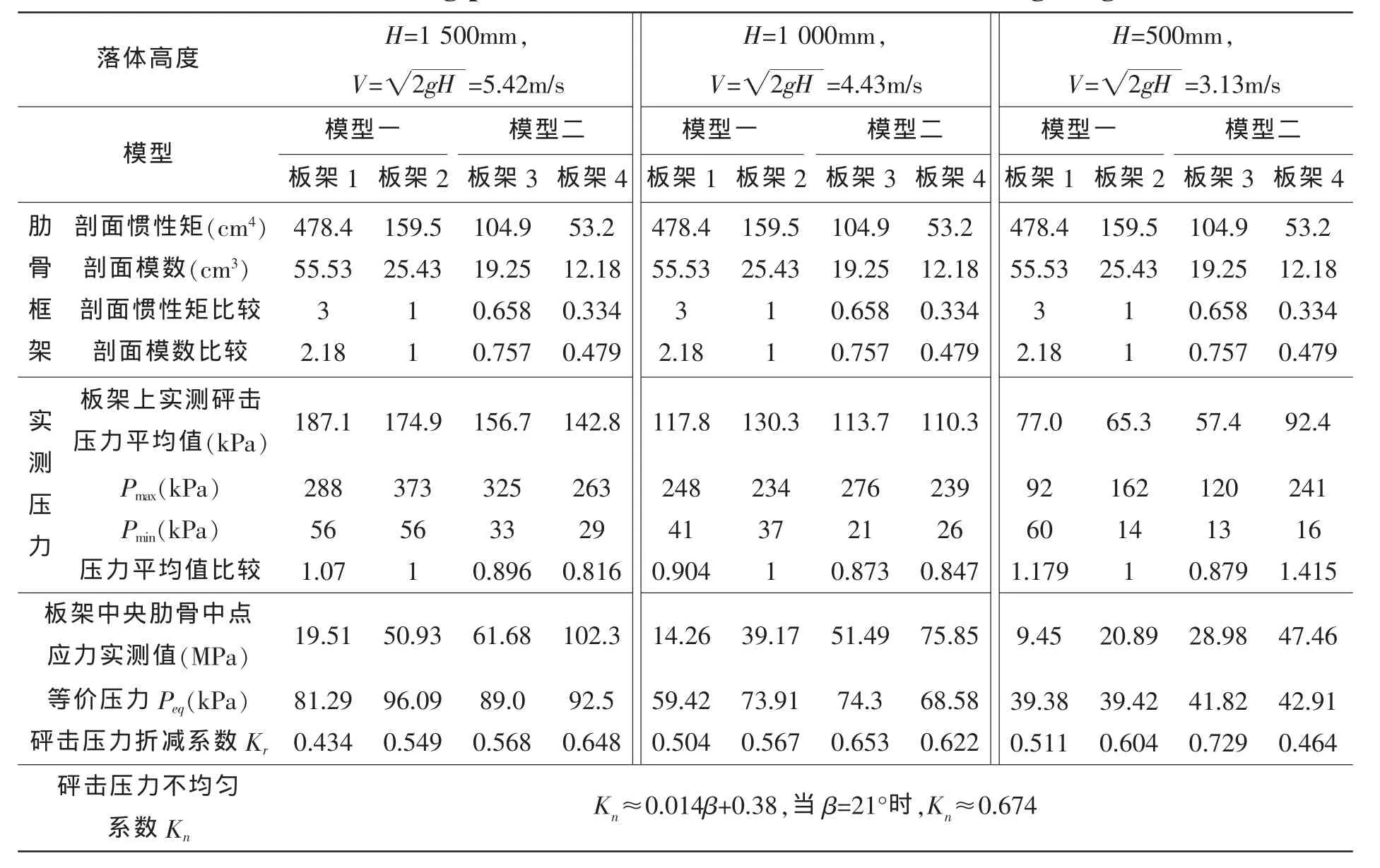
表4 試驗板架砰擊壓力與折減系數分析Tab.4 Slamming pressure and reduction factors of the test grillages

（3）對于板架1和板架2，砰擊壓力的變化規(guī)律大體上可視為剛體，而當剖面慣性矩和剖面模數降低為2/3后結構彈性對砰擊壓力的影響逐漸增大，尤其以最弱剛度的板架4最為明顯，其剖面慣性矩僅為板架2的1/3。

（4）在低速度落體沖擊工況下，砰擊壓力呈現(xiàn)一定的離散性，板架4的砰擊應力呈現(xiàn)異常增大。高速度落體沖擊工況則規(guī)律性較好。

5 結 論

本文通過變剛度楔形體板架的落體沖擊試驗以及對其結構的折減系數分析，可得結論如下：

（1）承受砰擊載荷的局部結構板架設計中，肋骨框架等效設計壓力與壓力“折減系數”的確定值得關注，通常根據實船結構以一定縮尺，按力學相似設計的結構模型，經落體砰擊試驗可以確定這個“折減系數”。

（2）砰擊壓力不均勻系數大體上反映“折減系數”的量級，而“折減系數”一般小于壓力不均勻系數，因此，在結構的初步設計中，可先根據砰擊壓力不均勻系數設計結構并采用適當的試驗手段取得相關結構的壓力“折減系數”，然后可進行詳細設計。

（3）當結構的剛度大幅下降時，彈性對砰擊壓力和結構動響應的影響會變得顯著。導致砰擊壓力的降低以及結構響應的增大，相應砰擊壓力“折減系數”也就增大。

[1]Faltinsen O M,Landrini M,Greco M.Slamming in marine applications[J].Journal of Engineering Mathematics,2004,48:187-217.

[2]ISSC.Committee V.7.Impulsive pressure loading and response assessment[C].17th International Ship and Offshore Structures Congress,16th-20th August 2009.Seoul,Korea,2009.

[3]王 輝.船舶砰擊載荷及局部結構動響應研究[D].無錫:中國船舶科學研究中心,2010.

[4]Hagiwara K,Yuhara T.Fundamental study of wave impact loads on ship bow,2nd Report-Equivalent static pressure of impact to structural reponse of a rectangular plate panel[J].J Soc.Nov.Arch,Japan,1974,11:337-342.

[5]Faltinsen O M.Sea loads on ships and offshore structures[M].Cambridge Ocean Technology Series,1990.

[6]Gu X,Hu J,Moan T,Design slamming pressures of a high-speed hydrofoil-assisted catamaran[C]//Fast 2001,4th-6th September 2001.Southampton,UK,2001.

[7]Kaplan P,Malakhoff A.Hard structure slamming of SES,craft in waves[C]//AIAA/SNAME Advanced Marine Vehicles Conference,17th-19th April 1978.San Diego,USA,1978.

[8]Wang H,Gu X,Shen J.The equivalent design pressure of ship frame structures under bottom slamming loads[C]//Proc.27th International Conference on Offshore Mechanics and Arctic Engineering.Estoril,Portugal,OMAE2008-58020,2008:197-202.

[9]王 輝.船體結構局部強度設計中的砰擊載荷確定方法[J].中國造船,2010,51(2):68-77.