材料衍生比例定律的建立及其在結構屈曲斷裂非線性失效中的應用

熊志鑫，張志平，佟福山

（1哈爾濱工程大學 船舶工程學院，哈爾濱 150001；2 DNV船級社 上海分部，上海 200336）

1 引 言

力學發展史表明，非線性問題的建模與求解是極其艱辛和費力的工作，需要大量繁復的力學推導和數學運算。近年來，隨著大型高速計算機的出現，國內外許多學者采用能量法、有限元法以及有限差分法對非線性的屈曲和斷裂問題作了諸多的數值分析。但由于大撓度帶來的幾何非線性和屈服所造成的物理非線性的耦合，使問題的分析變得非常困難，并導致計算花費的昂貴。為此，一方面，很多學者繼續采用對經典線性理論修正的方法來解決非線性問題；另一方面，人們對非線性理論本身進行反思。衍生比例定律就是綜合兩方面考慮而產生的必然結果。

2 衍生比例定律的建立和解析模型

2.1 衍生比例定律的理論依據

以切線模量因子為基本參數的強度穩定綜合理論可以較好地解決薄殼的承載能力問題和指導實驗[1]。隨著該理論的進一步發展，在疲勞、斷裂、灰色預測等領域得到了較廣泛的應用。因此，研究者對切線模量理論本身進行了反思。

文獻[2]利用應變能定理對切線模量理論進行了新的論證，并指出了其應用擴展的可能性。

文獻[3]進一步指出切影應變εt是與應變能密度相對應的平衡狀態參數，基于切影應變εt建立的材料衍生比例定律是用材料參數對材料試件的拉（壓）平衡狀態做出的數學描述，這種描述適用于各種材料和每一個拉（壓）平衡狀態。

文獻[4]把衍生比例定律概括為胡克定律（Hooke’s Law）的革新，稱其是材料固有的一種物理性質，它的使用不受材料比例極限的限制，是比胡克定律使用范圍更廣泛的一個基本定律。

衍生比例定律即是利用切線模量將各種線性理論轉化為相應的非線性理論，利用應力應變曲線上的物理參數建立了實際材料應力和理想彈性材料應力間相對應的函數關系。

2.2 衍生比例定律的建立

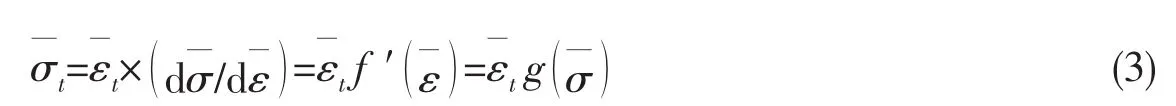
通過切影應變，實際應力可表示為利用理想狀態和實際平衡情況在每個極限平衡狀態下切影應變相等的內涵，可以建立實際應力和理想彈性應力的關系：

理想彈性應力已是經典理論研究比較透徹的，利用材料常數可以方便求得非線性的實際應力。

由于使用參數Φt表達材料應力應變曲線的廣泛性和方便性，所以采用基于切線模量因子Φt的函數來表達和求解實際應力。這將在下節中作進一步的說明。

2.3 衍生比例定律的解析模型

衍生比例定律數學模型的建立步驟如下：

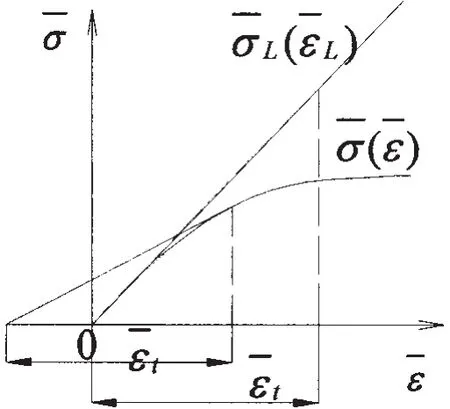
圖1 無量綱應力應變曲線Fig.1 Dimensionless stress-strain curve

（4）如果σL取得的是彈性失效應力，則對應的實際非線性應力為臨界失效應力：

也表達為 ψ=（A -B（ nφ）c）m，稱作強度利用率函數。其中，ψ表示結構失效時材料的強度利用率；φ=σ/σ，0E對應結構線性失效的參數；n是綜合因子，反映各種因素對結構穩定性的影響。

3 強度利用率函數ψ=的適用性

3.1 實例證明

文獻[6]通過引入一個六參數方程來描述材料應力應變的非線性關系，再分四組對其中幾個參數取常值進行簡化后，得到相應的四個強度利用率函數，（6）式正是這四個函數的通式。考察分組中的第Ⅱ種簡化方案[7-9]，利用得到的三參數方程分別對13種常用鋼材的應力應變關系進行曲線擬合，得到較高的擬合精確度，體現了六參數方程對材料的廣泛應用性。

文獻[10]通過研究大量的材料曲線指出，“以材料常數A，B，c和m來表示材料的非線性特征和各種不同材料之間的共性，是一種較好的表示方法”。

3.2 與潛水器規范表達的一致性

文獻[6]建議使用（8）式作為計算強度利用率的通式：

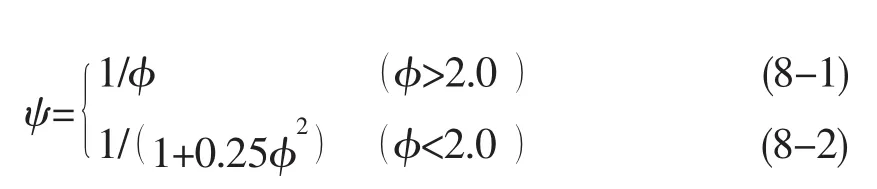
為便于比較，將（8-2）式轉換表達如下：

表達式（8）與中國潛水器規范[11]的物理修正曲線CS的比較如圖 2 所示。 由圖可知，在 φ＜0.8（即 σe/σS＞1.25）時，（8）式可以作為修正曲線CS的替代值使用。在σe/σS＞2.0時，三條曲線顯示出高度的一致性。

DNV規范對于耐壓殼塑性穩定性的修正系數：

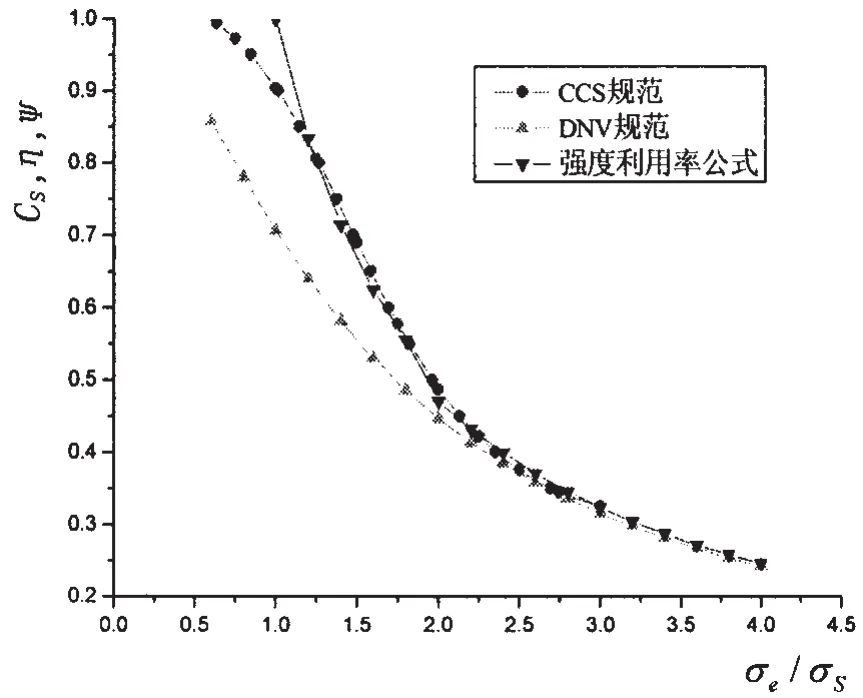
圖2 規范塑性修正系數值和公式（8）的比較Fig.2 Correction coefficient of non-linearity of three cases

則可通過取 A=1，B=1，c=-2，m=-1/2 得到。

4 衍生比例定律在結構塑性屈曲中的應用

近年來，深海載人潛水器在各國都得到了極大的重視和發展。隨著潛水器潛入深度的增加，厚度半徑比增大，球殼已屬于中厚球殼范圍。基于應變能定理立論的衍生比例定律是強度穩定綜合理論的新發展，適用于拉、壓作用下平衡狀態的任何構件，這也擴充了強度穩定綜合理論的使用范圍。所以，基于該定律計算潛水器耐壓殼極限承載能力，可以繼續對經典穩定理論中的臨界應力加以修正使用。

4.1 鈦合金球殼的強度利用率函數式

按照2.3節的步驟，可以得到深海載人潛水器耐壓殼的常用鈦合金材料在比例極限以上失穩時的強度利用率函數式：

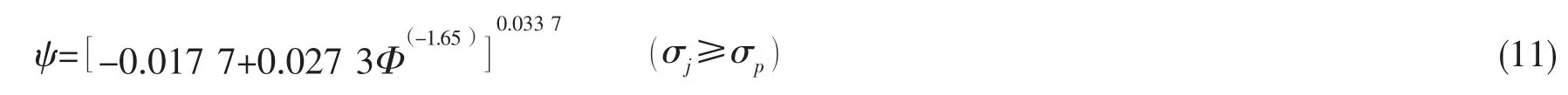
4.2 材料衍生比例定律算法的結果分析

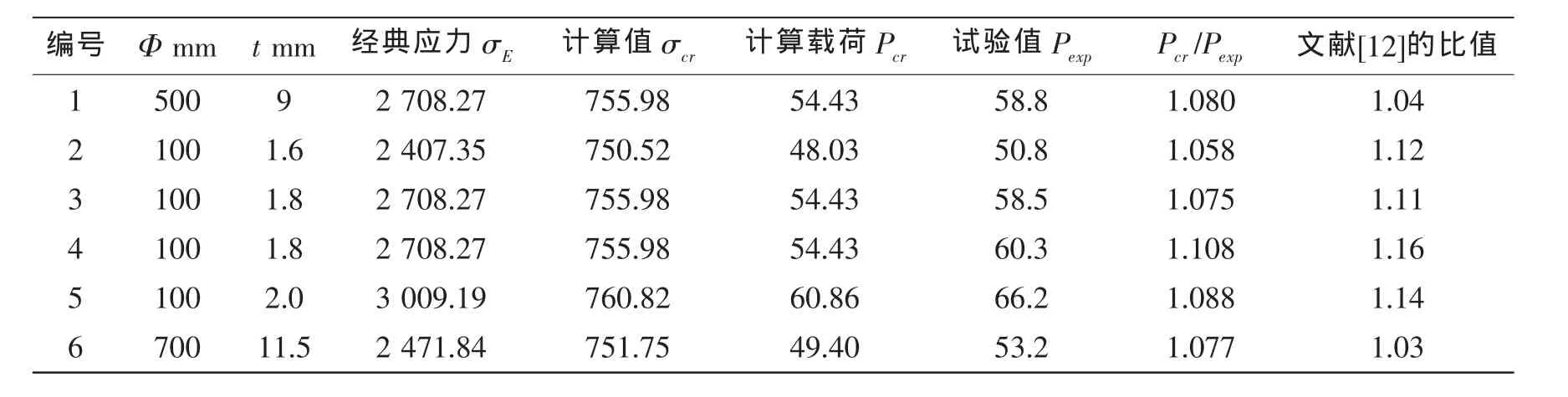
表1 計算值與試驗結果的比較Tab.1 Comparison between calculation values and experiment results

由表1可以看出，計算值與試驗結果誤差基本都在10%以內。與文獻[13]介紹的簡易算法相比，本文的方法立論于應變能定理，應用范圍更廣泛，使用也更為規范和方便。

4.3 結果誤差的調整和n的物理意義

上式中的計算值與試驗結果存在著誤差的原因在于：在實際中，由于工藝或實際需要，球殼總是存在著幾何缺陷、殘余應力等。這種影響可以通過引入系數n來量化。表1中，對n取2.55，則計算值與試驗值相對誤差都在5%以內。

n值的大小既可以通過理論分析算出，也可以統計試驗數據得出。通過n可以反映各種因素等對結構承載能力的影響。如果因素過多，則可以選取主要因素建立n的表達式

顯然，充分利用n值對實驗數據進行整理分析，可以達到通過少數模型實驗的方法確定多數原型極限載荷的目的。

5 衍生比例定律在彈塑性斷裂中的應用

根據裂紋端部塑性區尺寸的大小，彈塑性斷裂問題可以分為小范圍屈服斷裂，大范圍屈服斷裂和全面屈服斷裂。前者可以通過對應力強度因子修正后進行計算，后兩者則通過引入裂紋張開位移（COD）法和J積分的方法解決。利用衍生比例定律，可以代替或聯合上述的方法來解決彈塑性斷裂力學問題。

5.1 對應力強度因子KIC的修正使用

無限寬板Ⅰ型裂紋的線性斷裂臨界應力為：

利用（6）式，則對應的非線性斷裂臨界應力為：

文獻[14-15]驗證了（14）式是一些實驗統計經驗算式的通式。

5.2 與COD法的等效性

COD方法雖然缺乏嚴密的理論基礎和分析手段，但是由于它能簡單有效地解決實際問題，所以仍然得到了工程界廣泛的使用。在非線性臨界應力的計算中廣泛應用的COD法經驗近似值為：

取 Φt近似值 σs/σ，并聯合（6）式和（15）式，可得：

裂紋尖端張開位移值δc是一個材料常數，此常數和應力強度因子KIC有函數關系[16]：

聯立（5）、（13）和（17）式，可得和（16）式相同的表達。

通過5.1和5.2節的分析可知，衍生比例定律算法與修正KIC法、COD法的不同之處在于考慮了材料常數A，B，c，m對實際臨界應力的影響。

利用Φt數可以方便建立斷裂的非線性臨界應力表達式，這也從一個側面反映出采用參數Φt來表達應力應變曲線的優越性。

5.3 Φt與 J 積分的關系

J積分是與積分路徑無關的線積分。可以取其積分回路為以裂紋尖端為圓心，以r為半徑的圓，則可進一步簡化得到J積分的如下表達式[17-18]

式中Q為一個無因次的量，隨參考點的不同而變化。σ，ε是參考點處的應力和應變，參考點可在積分路徑Γ上任意選取，一般選便于計算的點。

當應變增加dε時，假設裂紋仍不擴展。對（18）式兩邊取微分并忽略高次項，得

（19）/（18）可消去參數 rQ，

引入無量綱數并對照（5）式，可得J與Φt的關系式：

由（2）式和（5）式可知，Φt與存在函數關系，所以可以通過 Φt～的關系式求 J 積分的值。

近年來，失效評定圖技術正經歷著由COD理論為依據轉向以J積分為依據。無論是EPRI（美國電力研究院）的失效評定圖還是CEGB（英國中央電力局）的新R6曲線，都加入了把材料應力應變曲線關系作為判定的基本參考條件。這也體現出和衍生比例定律研究思路的一致性。

6 結 論

（1）論證了強度利用率函數對絕大多數材料應力應變曲線的適用性。

（2）通過材料應力應變關系建立的衍生比例定律可以較好地解決結構的非線性失穩問題，尤其是方便計算大深度潛水器耐壓球殼或圓柱殼的極限承載能力。

（3）引入基于材料的平衡狀態參數Φt，可以與三種斷裂度量參數建立關系或等效使用，證明了該定律也可以在彈塑性斷裂力學中得到應用，但這方面進一步的研究需要更多試驗數據的參與。

（4）基于參數Φt建立的材料衍生比例定律可以解決屈曲和斷裂的非線性失效問題，繼而可以統一失穩和斷裂的雙準則失效問題。深入這方面的研究，從而解決實際結構的失效問題，將是一項很有意義的工作。

[1]羅培林.結構強度穩定綜合理論的梗概和意義[J].機械強度,1986,2:56-60.

[2]韓 蕓,羅培林,佟福山.切線模量理論的內涵和用途的擴展[J].中國造船,2008,49(3):98-103.

[3]張志平.廣義切線模量理論及其應用[D].哈爾濱:哈爾濱工程大學,2005:11-18.

[4]羅培林.Hooke’s Law（胡克定律）的革新與“強度穩定綜合理論”的創建和發展[J].哈爾濱工程大學學報,2008,29(7):641-650.

[5]羅培林.材料應力應變圖的相似性及其表達形式和應用[J].哈爾濱船舶工程學院學報,1984(1):9-22.

[6]羅培林.應力應變六參數方程及其在結構穩定性計算和實驗中的應用[J].中國造船,1981(3):65-75.

[7]雒高龍,張淑茳,任慧龍.船用鋼應力—應變關系的數學表達及其在計算加筋板屈曲應力中的應用[J].造船技術,2006,3:13-19.

[8]張淑茳,石德新,姜志慶,佟利軍.某種新的高強度鋼非線性品質的研究[J].哈爾濱工程大學學報,1996,17(4):62-66.

[9]張淑茳,萬 磊,石德新.材料非線性性質的解析表達[J].固體火箭技術,1996,19(2):71-78.

[10]石德新.結構承壓能力的模型實驗原理和方法[D].哈爾濱:哈爾濱船舶工程學院,1990:10-41.

[11]中國船級社.潛水系統和潛水器入級與建造規范[S].北京:人民交通出版社,1996:31-42.

[12]劉 濤.深海載人潛水器耐壓球殼設計特性分析[J].船舶力學,2007,11(2):214-220.

[13]劉 濤.大深度潛水器耐壓殼體彈塑性穩定性簡易計算方法[J].中國造船,2001,42(3):8-14.

[14]Luo P L.Relationship between critical stress coefficients of buckling and fracture and its signification[C]//Proceedings of Sixth Pacific Structural Steel Conference.Beijing,China,2001(10):15-17,251-259.

[15]戴 光,劉康林,齊文浩.結構斷裂強度研究的切線模量因子法[J].大慶石油學院學報,1999,23(2):53-56.

[16]李志安.壓力容器斷裂理論與缺陷評定[M].大連:大連理工大學出版社,1994:57-63.

[17]Broek D.The Practical Use of Fracture Mechanics[M].Kluwer Academic Pulished,Dordrecht/Boston/London,1988.

[18]劉康林.結構失效分析的強度穩定綜合理論法研究[D].哈爾濱:哈爾濱工程大學,1996:46-55.