一種新的基于四點插值細分的圖像修復算法

韓翠英，段琳琳

HAN Cui-ying1，DUAN Lin--lin2

（1.安陽工學院，安陽 455000；2.鄭州大學，鄭州 450001）

0 引言

圖像破損以及數據丟失是圖像經壓縮、傳輸、解壓縮過程中經常遇到的問題，這一問題已經引起圖形圖像處理研究人員的廣泛關注，圖像破損中較為嚴重的情況是像素群丟失，如圖像經編碼后在傳輸中受到干擾而出現解碼后的像素群丟失，或由解碼技術本身決定的圖像不能完全復原。針對單像素丟失，常見的解決方法為簡單的鄰點平均法和中指濾波法。對像素群丟失的情況則問題比較復雜，只能根據待修復區域適當范圍內的像素所含信息通過建立的修復規則進行修復，要想完全修復是不可能的。

1 基于四點插值細分模式的修復算法

1.1 細分細則

插值面分裂型細分方法是指用于規則四邊形網格時，其細分規則是曲線四點插值細分模式通過張量積形式的自然推廣，對于非正規四邊形網格采取特殊的細分規則。通過一定規則作用到舊網格上產生新網格，通過網格不斷加細最終生成光滑曲面。該插值面分裂型細分方法的細分規則是曲線四點插值細分模式通過張量積形式的自然推廣，對于非正規四邊形網格采取特殊的細分規則。通過一定規則作用到舊網格上產生新網格，通過網格不斷加細最終生成光滑曲面。新網格的生成規則包括兩部分，即幾何點的產生和拓撲結構的建立。新的幾何點包括新邊點、新頂點、新面點，新邊點是對應邊的兩端鄰近四個頂點的加權平均；新頂點等于舊頂點；新面點是對應面上所有頂點及周圍的一些點的加權平均。其拓撲結構依如下規則建立，連接每一新面點與其周圍的新邊點；連接每一新頂點與其周圍的新邊點。

1.2 對破損圖像區域的預處理

設二元函數z=f（x,y），定義區域為D，值域為G。我們把圖像中的像素點位置集合視為空間曲面的定義區域，即二元函數z=f（x,y）中的D；把圖像中像素點處的灰度值與空間曲面的函數值相對應，即二元函數z=f（x,y）中的G。由于圖像所反映的是現實的世界，因此除邊緣（輪廓）部分外，圖像中像素的灰度值一般可看作是連續變化的，這樣就可以采用曲面四點插值細分模式的細分規則。進行插值，恢復其灰度值。這樣做的優點在于能夠合理而有效地利用破損像素塊周圍像素灰度特點構造未知像素的灰度值，且由四點插值細分理論，二元函數z=f（x,y）在該部分的灰度函數具有一階連續性。但如果破損像素塊包含邊緣像素時，利用曲面細分模式進行插值修復，導致修復后圖像邊緣被過度光滑，修復效果不理想。因此，在進行圖像修復前，需要對圖像進行預處理，判斷破損區域是否存在邊緣像素。

利用求破損圖像周圍的各鄰點（所謂鄰點是指距破損區域邊緣最近的非丟失的像素點）梯度的方法，判斷破損圖像周圍像素的灰度變化情況，即檢測出在破損圖像區域中可能包含的邊緣像素點。如果存在邊緣點，找出其邊緣的走向，利用四點插值細分規則的邊點計算方法對邊緣像素進行修復，然后再用曲面細分規則對其它區域進行修復。若破損圖像區域中不包含邊緣點，則直接利用曲面細分規則對破損區域進行修復。

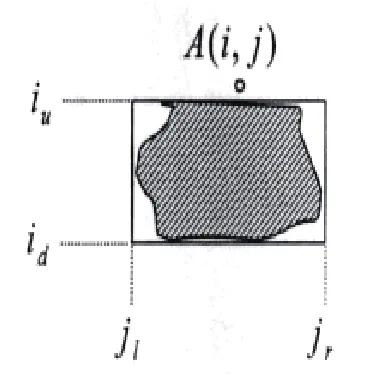
圖1 假設破損圖像區域

假設破損圖像區域如圖1所示。圖中陰影部分為破損區域，為了便于處理，將破損區域外推成矩形區域，并視為待修復的破損區域，該區域所包含的像素為 。設破損區域的某一鄰點A的坐標為（i,j），破損圖像區域的左上角的坐標為（iu,jl），右下角的坐標為（id,jr）如圖1所示。

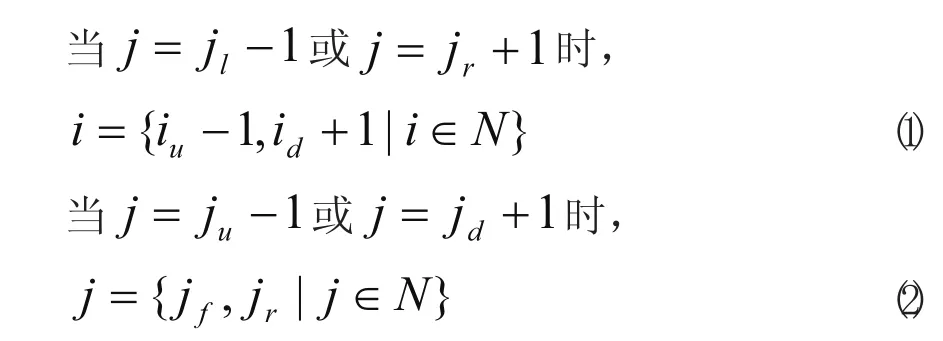
當按（1）、（2）式給出的i，j值，可以取遍破損圖像區域的所有鄰點。對像素點A（i,j），求其梯度幅值和其梯度幅角為：

對于所有的破損區域的所有鄰點，由公式（3）、（4）得到所有破損圖像區域的鄰點的梯度幅值和梯度方向的集合{G（i,j}和{θ（i,j}。為避免修復的復雜性和減少計算量，對梯度幅值設置一個閩值k，然后，將G（i,j）和闡值k進行比較。如果梯度幅值G（i,j）大于k，則該像素點（i,j）被認為是階躍點（或稱為邊緣點）；反之則認為為光滑點。如果破損圖像區域位于圖像的邊緣處，通過這樣的比較，即可留下破損圖像區域鄰點的邊緣像素點。對所有的這樣的像素點進行線插補后，再對剩余區域按曲面插值算法進行修復；如果破損區域位于圖像的光滑區域，則跳過線插值修復，而直接進行曲面插值修復。

1.3 基于四點插值細分模式的修復算法

為了說明這種算法，我們假設有一邊緣破損區域的圖片，如圖2所示。其中“。”表示待修復的像素，“。”為破損圖像區域外圍的己知像素，“。”為面點和邊點，并以已知A的坐標，設圖像的灰度值用f（x，y）表示，x，y為像素的坐標；初始層k=0。

圖2 假設一邊緣破損區域圖

具體的曲面四點插值細分模式用于破損圖像修復的算法如下：

1）根據破損區域的像素個數和破損區域的外鄰點A求待修復區域中的中間像素點（面點）的位置，設求得面點S的坐標為（i,j），距A的距離（像素點個數）為p，q，則可用面點S的坐標和p,q將A點表示為A（i-p,j-q）。

2）以p,q為步長，以S點為基準，在破損區域周圍取如下16個已知像素點（取點是按曲面四點細分規則進行的），即：f（i-3p，j-3q），f（i+3p，j-3q），f（i+3p，j+3q），f（i-3p，j+3q），f（i-p，j-3q），f（i-p，j+3q），f（i+p，j-3q），f（i+p，j+3q），f（j-3P，j-q），f（i-3P，j+q），f（i+3P，j-q），f（i+3P，j+q），f（i-p，j-q），f（j-p，j+q），f（i+p，j-q），f（i+p，j+q）。然后計算面點S的灰度值。

3）以新計算的面點S為已知點，計算面點。該步需要計算出四個新邊點，如圖4所示。具體算法這里以B點為例進行說明。為計算邊點B的灰度，首先計算出B點在該行破損區的位置，該點的坐標為（i，j+q/2），然后，按照邊點細分規則取如下四點f（i，j-2，），f（i，j-q），f（i，j）（由第二步計算出的面點），f（i，j+q）。再計算出邊點B的灰度值f（i，j+q/2）。同理可計算出其它三個邊點。

4）使k=k+1，利用第二步和第三步計算的面點、邊點為己知點，計算k+1的面點和邊點。為計算第k+1層的面點、邊點，將破損區域劃分22k個區域，并根據不同的區域調整A點的位置，并使p=p/2，q=q/2。

5）返回第一步，計算22k個區域的面點和邊點，直到p，q的值小于1為止。

1.4 算法仿真結果

為驗證算法的有效性，本文對lena圖進行了人為的損壞，破損區域大小均為7×7，并包含了平滑區域和含有邊緣區域，如圖3所示。由圖中可以看出，修復后的圖像和原始圖像的效果非常接近，因此驗證了本文所提出的四點插值細分模式用于破損圖像的修復算法是有效的，恢復后的圖像的質量也是優良的。

圖3 對本文算法的驗證圖

2 結論

本文提出一種新的基于四點插值細分的圖像修復算法，該方法來源于計算機輔助幾何設計研究領域中三維空間自由曲線曲面造型技術。使用該方法不僅可以修復不規則像素群，而且修復邊緣具有很好的平滑過渡性，但如果圖像破損處的灰度有階躍或近似階躍變化時，我們用梯度方法對破損圖像周圍的邊緣像素點進行檢測，對破損區域中包含的邊緣像素點按照四點插值細分模式中的邊點計算規則進行單獨處理，在破損圖像修復中得到了較好的結果。

[1]檀結慶,汪忠慶.一種新的基于鄰近像素點的圖像修復算法[J].合肥工業大學學報（自然科學版）,2006,29（9）：1072-1076.

[2]周春霞,吳錫生.基于方差和邊緣插值的鄰近點圖像修復算法[J].計算機工程與應用,2008,44（14）：184-186.

[3]張智豐,張亞榮.細分曲線參數化與累加弦長參數化的數值比較[J].湘潭師范學院學報（自然科學版）,2009,31（4）.