一類混雜系統的預測控制設計

鄒媛媛 賈廷綱 牛玉剛(.華東理工大學 信息科學與工程學院，上海 0037;.上海電氣集團股份有限公司中央研究院，上海 0003)

0 引言

分段線性(Piecewise Linear，PWL)系統作為一類基本的混雜動態系統模型，能夠用來描述許多工程實際系統中的混雜特性，如飽和、繼電器、死區等環節［1，2］，也可以用來近似非線性系統。因此，對PWL系統控制問題的研究具有重要的理論和實際意義。

目前，預測控制已經被成功應用于 PWL系統［3-7］，其中，PWL系統預測控制的穩定性綜合問題是大家關注的焦點［5，6］。針對這個問題，本文對含有兩個子系統的連續時間PWL系統進行預測控制器設計。首先，對每個子系統，設計有界控制器，在此基礎上，提出一種預測控制和有界控制相結合的混合控制方法，并給出子系統之間的穩定切換規則，從而保證系統的全局穩定性。這種方法的好處是只需要對每個子系統求解二次規劃問題，避免了對整個PWL系統求解含有邏輯變量的二次(或線性)規劃問題，降低了算法的復雜度。

1 有界控制

考慮如下的連續時間PWL系統

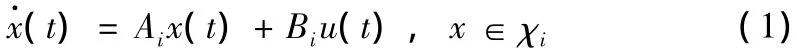
其中，x(t)=［x1(t)…xn(t)］T∈Rn是狀態向量，u(t)=［u1(t)…um(t)］T∈U?Rm是控制輸入向量。U是輸入約束，定義為U∶=系數矩陣分別為 Ai∈Rn×n，Bi∈Rn×m，i∈

考慮第i個子系統，設其Lyapunov函數為Vi=xTPix，存在滿足Ricatti方程

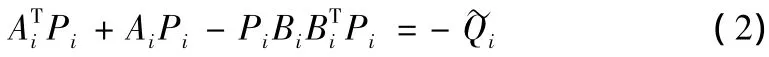
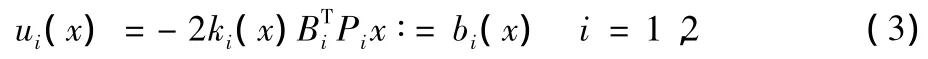
其中

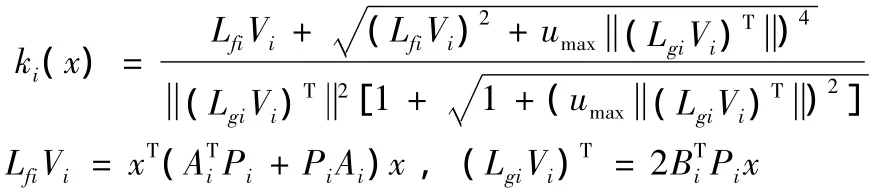
我們發現，如果狀態軌跡滿足如下條件

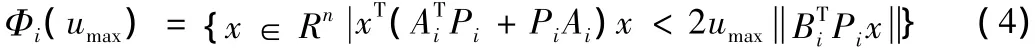
那么，根據Lyapunov理論，有界控制器(3)滿足輸入約束，并且Lyapunov函數是單調遞減的。利用集合Φi(umax)，可以構造一個包含在Φi(umax)的最大橢圓集作為穩定域

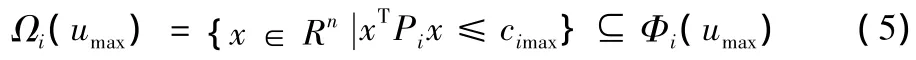
其中，cimax＞0是滿足Ωi(umax)?Φi(umax)的最大值。

對于系統(1)來說，穩定域估計集可以如下構造。假設S∶?為狀態分區的邊界

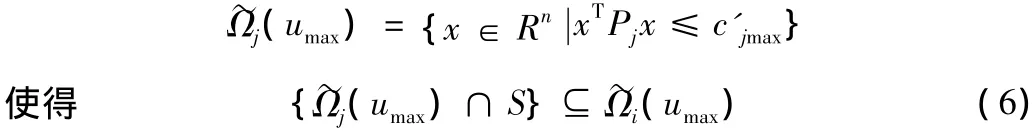
其中，c'jmax是滿足條件的最大值。則系統(1)的穩定域估計集

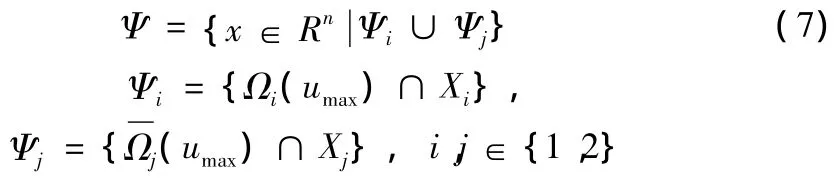
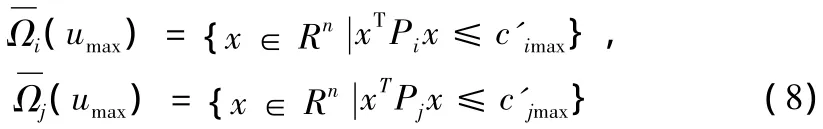
使得

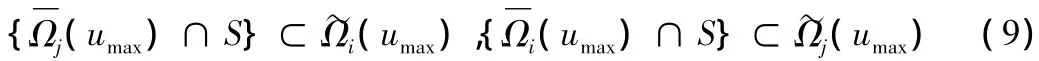
其中，c'imax、c'jmax是滿足條件的最大值。則含系統(1)的公共的穩定域估計集為(7)的形式，

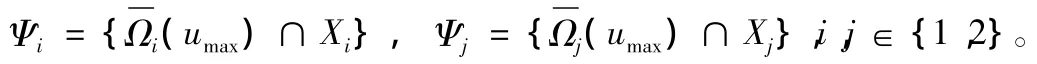
定理1 考慮系統(1)，對第i個子系統，通過構造Lyapunov函數Vi，得到該子系統的有界控制器(3)，穩定域估計集Ψ。假設初始狀態為 x0∈Ψi，i∈{1，2}。如果在時刻

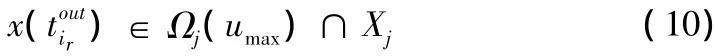
那么狀態切換到第j個子系統，反復此控制過程，可得閉環系統是漸近穩定的。其中是第r次離開第i個子系統的時間為第m次進入第j個子系統的時間為第m-1次進入第j個子系統的時間。

雖然定理1給出的有界控制策略能夠保證閉環系統穩定，但是，有界控制對系統的最優性沒有要求，因此在有界控制的作用下系統的控制性能較差。

2 混合預測控制

由于預測控制是在最優性能指標的情況下，求解滿足系統狀態和輸入約束的控制律，因此，其具有良好控制性能。基于上述分析，本文將預測控制和有界控制相結合，在系統的穩定域估計集內，采用兩種控制律切換模式以達到系統穩定性和最優性的兼顧。

2.1 子系統預測控制

針對系統(1)的每個子系統，設計相應的預測控制器。考慮第i個子系統，x(t)為系統在t時刻的狀態，可以通過求解如下優化問題得到預測控制

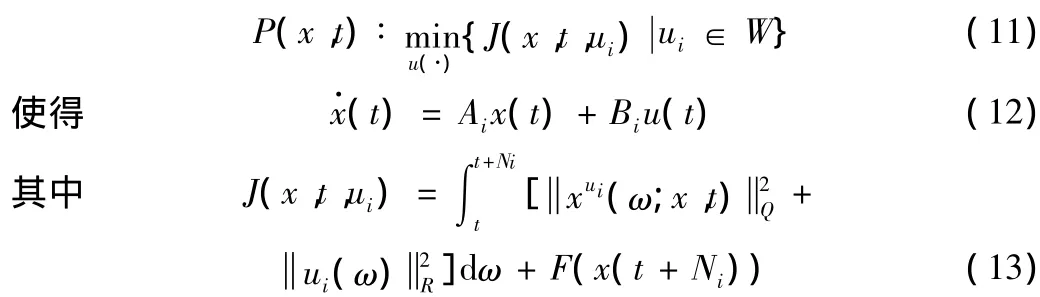
W=W(t，Ni)是一組由［t，Ni］映射到 U 的分段連續函數，Ni是預測時域，{ui［k］=ui(kT)}為要求的控制序列，滿足:ui(·)∈W ，ui(t)=ui［k］，t∈［kT，(k+1)T］，T 為采樣周期。xui(ω;x，t)是式(12)的解，Q和R是嚴格正定對陣矩陣，F是終端加權。

在時段［kT，(k+1)T］內，通過求解上述優化問題，可以得到一組預測控制序列。通常我們只采用第一個(·)∈W，即

作用到第i個子系統。

2.2 混合預測控制

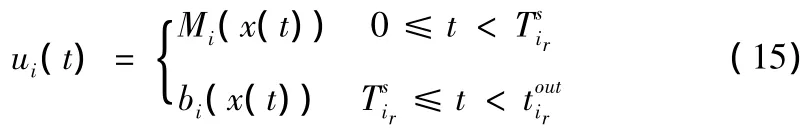
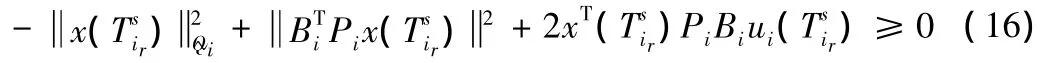
3 仿真研究

為了驗證混合預測控制的有效性，考慮下面例子

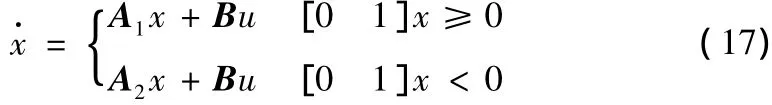
針對(17)描述的兩個子系統，分別考慮對應的Lyapunov函數 xTPix。取，通過求解 Ricatti方程，可知

根據(7)的描述形式，系統(17)的穩定域估計集，預測控制目標函數的參數選擇為 Q=2×I2，R=0.1，時域長度 T=0.4。取初始狀態為x0=［23］T∈Ψ1，采用定理2提出的混合預測控制策略，閉環系統狀態軌跡漸近到達原點。

4 結論

本文針對一類混雜系統，提出了一種保證閉環系統穩定性的預測控制策略。對每個線性子系統，分別設計相應的有界控制器，并在此基礎上，基于子系統之間的狀態切換條件構造出系統的穩定域估計集。在穩定域估計集內，給出有界控制和預測控制相結合的控制策略，保證了不同子系統之間切換的穩定性。

［1］ SONTAG E.Nonlinear regulation:The piecewise linear approach［J］.IEEE Transactions on Automatic Control，1981，26(2):346-358.

［2］ 張聚.混雜系統理論及在非線性系統中的應用研究［D］.浙江大學，2005.

［3］ 鄒媛媛，鄒濤，李少遠.混雜系統的預測控制.控制與決策，2007，22(4):361-365.

［4］ 丁寶蒼.預測控制的理論與方法［M］.北京:機械工業出版社，2008.

［5］ 曾鋒，高東杰，李秀改.一類有約束的分段線性系統雙模預測控制.控制與決策，2006，21(5):597-600.

［6］ ?ZKAN L，KOTHARE M V，GEORGAKIS C.Model predictive control of nonlinear systems using piecewise linear models［J］.Computers and Chemical Engineering，2000，24(2-7):793-799.

［7］ LAZAR M，HEEMALS W P M H.Predictive control of hybrid systems:Input-to-state stability results for sub-optimal solutions［J］.Automatica，2009，45(1):180-185.

［8］ El-Farra N H，Mhaskar P，Christofides PD.Uniting bounded control and MPC for stabilization of constrained linear systems［J］.Automatica，2004，40(1):101-110.