在活動中感悟數學:以多邊形內角和的教學為例

●郜青林 (溫嶺市第九中學 浙江溫嶺 317520)

在活動中感悟數學:以多邊形內角和的教學為例

●郜青林 (溫嶺市第九中學 浙江溫嶺 317520)

《義務教育階段數學課程標準(修訂稿)》強調:學生學習應當是一個生動活潑的、主動的和富有個性的過程．除接受學習外，動手實踐、自主探索與合作交流同樣是學習數學的重要方式．學生應當有足夠的時間和空間經歷觀察、實驗、猜測、計算、推理、驗證等活動過程．在這樣的數學活動中，讓學生經歷從不同角度尋求分析問題和解決問題的方法的過程，體驗解決問題方法的多樣性，掌握分析問題和解決問題的一些基本方法．并在與他人合作和交流過程中，更好地理解他人的思考方法和結論．下面筆者結合《多邊形內角和》的教學設計，例談如何組織開展數學活動．

1 基于學生的知識基礎，提出活動問題

重視研究學生原有的知識基礎．任何新知識都是舊知識的延伸發展，因此教師要認真深入研究學生學習新知識所必備的知識基礎及舊知識的掌握狀況．即已經知道什么，哪些知識掌握得較扎實，哪些知識掌握得較模糊等，從而確定教學的途徑、方法．因為學生在小學階段已經初步掌握了三角形的內角和及正方形和長方形的內角和等知識，所以筆者在“多邊形內角和”的教學導入是這樣設計的:

師:大家還記得三角形的內角和是多少度?

生:180°．

師:正方形、長方形的內角和呢?

生:360°．

師:任意一個四邊形的內角和是否也是360°?

生:……(給學生1分鐘左右的時間思考)．

設計意圖從學生的實際出發，開門見山地談到了本節課需要的知識基礎“三角形的內角和”，同時也給學生留下了思維的空間．既重視全體學生的學情，又重視個別學生的學情，有利于因材施教．

2 利用學生的已有經驗，探究新知識

孔子曾說過:“不憤不啟，不徘不發”．教師作為一個啟發者、引導者，應為學生根據所學知識巧妙設計問題，使學生產生“心欲求而未得，口欲言而不能”的積極進取狀態，讓學生達到“憤悱狀態”．激發學生的求知欲，調動學生積極主動地探索、分析、解決問題．可采用多種方式引導探索，讓學生先通過嘗試、探索思考，然后講解引導獲得新知識;或先猜后證，即學生先通過大膽猜想發現結論，然后教師引導證明;亦或學生先動手實驗，進行觀察、分析從而發現規律，然后教師引導尋求結論．在此過程中，教師要適時點撥充分發揮主導作用．在拋出問題“任意一個四邊形的內角和是否也是360°”后，可以進行如下引導:

師:(點撥)大家能利用三角形內角和去研究四邊形的內角和等于360°嗎?

生:……(給學生1分鐘左右的時間思考)．

師:(點撥)用三角形的知識去證明四邊形的知識，關鍵是什么?

生:只要將四邊形分成幾個三角形即可．

師:請同學自己動手試試，分好后再簡易推理四邊形的內角和是不是360°．

(分小組，放手由學生自己去實踐，教師掌握各組的進程，并作指導．)

展示學生的幾種方案如下:

生1:連結一條對角線，如圖1所示．把四邊形分成2個三角形，四邊形 ABCD的內角和等于△ABD的內角和與△BCD的內角和之和，即180°+180°=360°．

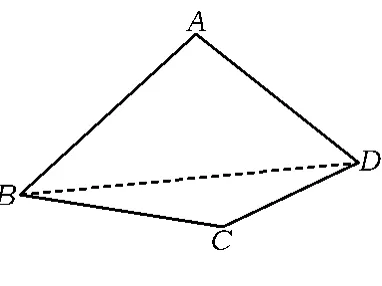
圖1

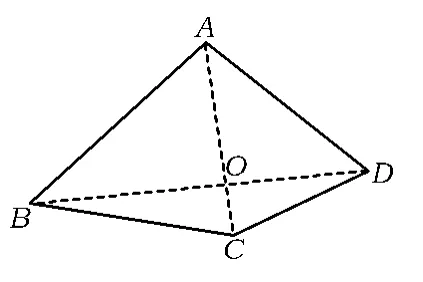
圖2

生2:連結2條對角線，如圖2所示．把四邊形分成4個三角形，則四邊形ABCD的內角和等于△ABO，△BCO，△DCO，△ADO的內角和之和減去360°，即180°+180°+180°+180°－360°=360°．

(教師提出:若點O不是對角線的交點，則可以嗎?點O在邊上或在四邊形的外部，又如何推理呢?如圖3，推理過程此處略．)

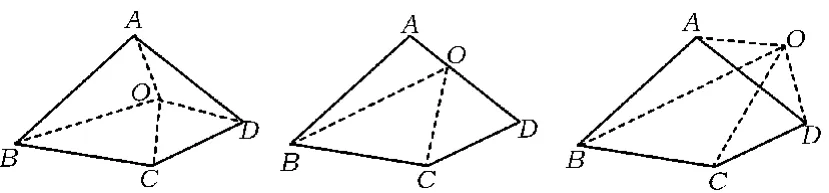
圖3

圖4

生3:不考慮交點的位置也可以證明．如圖4所示，四邊形ABCD的內角和=△AEG的內角和+△EBF的內角和+△EFG的內角和+△FDG的內角和+△FCD的內角和－180°－180°－180°=180°+180°+180°+180°+180°－180°－180°－180°=360°．

設計意圖該設計注重培養學生的能力，同時也體現了教師的主導作用．以學生為本，把課堂還給了學生．只有這樣，學生的頭腦才真正動起來，才能真正地參與到知識的發現過程中來，我們的教學才能真正做到注重過程而不是結論．

3 引導學生歸納活動過程，拓展知識

通過對任意四邊形內角和的探究，學生已經找到了研究多邊形內角和的最簡單辦法．教師應該趁熱打鐵，幫助學生總結方法并加以拓展，可以作如下設計:

師:大家分得很好，這說明用三角形的知識去研究四邊形的方向是正確的，也足以說明任何四邊形的內角和都是360°．大家回顧一下剛才的作圖，哪種分法及推理更簡潔呢?

生:生1的分法更簡潔．

師:生1的作法就是從一個頂點引對角線，從而分成了2個三角形．那么大家考慮:從五邊形的一個頂點出發，可以引幾條對角線?它們將五邊形分為幾個三角形?五邊形的內角和等于180°乘以幾?

同時，在屏幕上打出從五邊形一個頂點出發，可以引＿＿條對角線，它們將五邊形分為＿＿個三角形，五邊形的內角和等于180°×＿＿ ．．

生:2條對角線，3個三角形，乘以3．

師:請大家完成屏幕上的表格，如表1所示．

表1 對角線數、三角形數與內角和

師:從表格上你發現什么規律?

生:從一個頂點畫的對角線的條數比邊數少3，分成三角形的個數比邊數少2．

師:為什么會這樣呢，是不是任意多邊形都有這個規律，能推理嗎?

生:在畫對角線時，不能往點的自身及和它相鄰的2個點引，故此比邊數少3;而除與這個頂點相鄰的2個邊外的邊都對應一個由對角線分這個頂點而成的角，剛好有邊數少2個三角形．

師:你觀察得很仔細，那么大家可以說出100邊形的相應數值嗎?

生:97條，98個三角形，內角和為98乘以180°．

師:那n邊形呢?

生:(n－3)條，(n－2)個三角形，內角和為(n－2) ×180°．

師:大家通過學習得到了多邊形的內角和為(n－2)×180°，其中n表示的是什么?

生:邊數．

師:對，n表示多邊形的邊的條數．在研究一個復雜問題時，通常可以轉化為從簡單問題入手來研究，去尋求規律，從而使復雜問題得以解決．

設計意圖通過由一個頂點出發引多邊形的對角線是分割多邊形為三角形，探求多邊形內角和的最簡單方法入手，是研究問題的一般規律，也是探求復雜問題結論的一種方法，潛移默化地培養了學生解決問題的能力．

從三角形的內角和到多邊形的內角和，在教學中通過分圖活動以及師生的共同探究，讓學生感受一種研究問題的一般方法，從特殊到一般的經歷，體會數學的轉化思想．因此，在教學時，教師一定要掌握知識發生的淵源，盡可能地給學生創造數學活動的機會，培養他們探究的習慣．其實，只要我們在教學活動上多花點功夫，經常反思活動成效，讓學生在課堂上體驗做數學的樂趣，品嘗做數學的快樂，課堂教學就一定能高效率地開展起來，也能得到更好的教學效果，從而實現輕負高質的愿望．