不同應力水平下結構性黏土動力特性試驗研究①

雷華陽，劉景錦，霍海峰

（1.天津大學 土木工程系，天津 300072；2.濱海土木工程結構與安全教育部重點實驗室（天津大學），天津 300072）

0 引言

為解決城市交通擁擠問題，大力發展城市快速路、城市輕軌、城市地鐵已成為每個城市的重點工程。但是對于東部沿海地區深厚軟黏土地質條件，由于受到車輛荷載作用軟黏土會產生較大變形和差異沉降，已有多個由于行車振動荷載作用而導致基礎破壞的實例。如何正確認識這種現象、解決這種現象是每位巖土工程工作者急需解決的難題，也是天津濱海新區大面積開發建設所面臨的重要的實際工程難題之一。

近年來，隨著人們對于土體結構性重視程度的增加，不同應力水平下結構性軟土的變形特性成為諸多學者研究的熱點之一。然而這種研究多集中于利用室內壓縮試驗分析土體在不同壓力階段的靜力學特性，無法獲得其動力特性變化規律。

許多學者曾對循環荷載作用下土體變形問題開展過研究。如Diyaljee和Raymond在靜止應力－應變數據和反復荷載試驗的最小循環次數數據的基礎上，建立了一個預測長期反復荷載作用下永久變形的方案［1］；Behzadi和Yandell采用矩形波的形式進行加載，提出了一個預測路基土永久變形的模型［2］；王建榮等通過動三軸試驗研究振動頻率對原狀黃土動本構關系的影響［3］；周建建立了綜合反映軟黏土孔壓變化和應變軟化的彈塑性模型［4］；鐘輝虹通過一系列應力控制的循環三軸試驗，分析研究了軟黏土在不排水條件下循環荷載作用下的累積殘余變形規律［5］；Sakai和 Miura提出了一個模擬不同圍壓下軟黏土部分排水特性的模型［6］，顧中華等提出循環荷載作用下飽和粘土強度計算方法以及參數的確定方法［7］；黃茂松等通過不同靜偏應力和動應力組合情況下的飽和軟黏土不排水循環三軸試驗，引入相對偏應力水平參數，分析給出了累積變形特征方程式［8］。

前人的研究成果側重于應力－應變本構關系及變形規律的描述，很少涉及到應力水平對軟黏土動力變形特性的影響規律。為了進一步了解應力水平對結構性軟黏土動力變形特性的影響，本文針對天津濱海新區典型軟黏土在不同固結應力下進行循環三軸試驗，探討不同應力狀態下土體的動力變形規律，以加深對結構性飽和軟黏土在動力荷載作用下變形特性的了解。

1 試驗土樣和試驗方法

1.1 試驗土樣

天津濱海地區分布有廣泛海相沉積的淤泥質黏性土，具有較強的結構。試驗取用濱海新區典型的淤泥質粉質黏土，取樣深度為4～8m，基本的物理力學指標如表1所示。

表1 試驗用土的基本物理力學指標

1.2 固結試驗

固結試驗采用的設備為杠桿式高壓固結儀。固結壓力采用12.5kPa、25kPa、50kPa、100kPa、200 kPa、300kPa、400kPa、800kPa、1600kPa加荷等級，進行不同固結壓力條件下的卸荷－再加荷過程。土樣面積為30cm2，高度為2cm。

1.3 動三軸試驗

為研究應力水平和土體結構性對軟黏土動力特性的影響，以壓縮試驗測定的原狀軟黏土先期固結應力和結構屈服應力為分界點，選取不同固結應力對原狀土樣進行動力試驗。

試驗儀器選用英國GDS動三軸試驗系統，固結應力分別為小于先期固結應力σv0、先期固結應力σv0與結構屈服應力σvy之間以及大于結構屈服應力σvy。振動頻率為1Hz、2Hz和5Hz。土樣高為10 cm，直徑為5cm。

2 結構性軟黏土的先期固結應力和結構屈服應力

土的先期固結應力是指土層在歷史上受到的最大豎向有效固結壓力。土的結構屈服應力是指原狀土在受壓縮過程中，以土骨架彈性壓縮為主的變形階段基本結束，土的結構和粒間聯系開始出現破壞時所對應的壓力。

眾多研究表明，軟黏土作為一種典型的結構性土，用傳統方法測得的先期固結應力值往往大于其上覆土層的應力，這就給判斷其固結狀態帶來了一定的困難。因此，沈珠江指出，這類土的原狀土壓縮曲線的拐點所對應的應力應稱為結構屈服應力而不應稱為先期固結應力［9－11］。超固結比應為結構應力比。

對于室內壓縮試驗曲線，許多學者都提出校正方法，這里結合郝玉龍等［12］針對溫州結構性軟土所提出的確定原位壓縮曲線及土體結構屈服應力的方法，確定天津濱海地區典型軟黏土的先期固結應力σv0和結構屈服應力σvy。結果見圖1和表2所示。

表2 土樣的先期固結應力和結構屈服應力

3 軟黏土在不同固結應力狀態下的動力特性

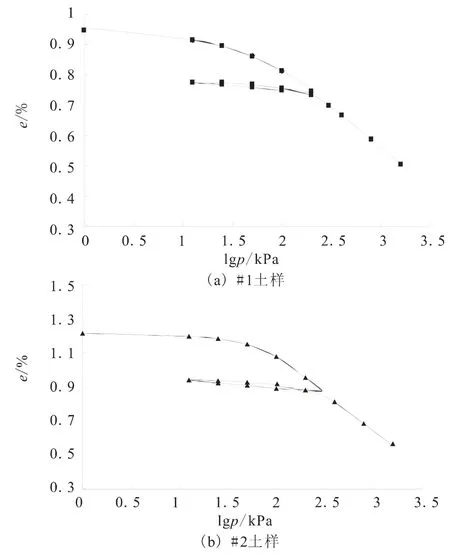
圖1 原狀土樣的壓縮曲線Fig.1 Compression curves of natural soft clay samples.

前面指出天津濱海地區軟黏土具有明顯的先期固結應力σv0和結構屈服應力σvy，為了解結構性軟黏土在不同應力水平下的動力變形特性，利用同種土樣以這兩個關鍵應力點為界限，進行了循環三軸試驗。

3.1 不同固結應力下的動應變－循環振次關系

圖2、3為原狀土樣＃1和＃2的軸向動應變－循環振次關系曲線。從圖中可以看出，在初期的循環荷載作用周數內，無論動應力多大，土樣的軸向動應變εd均表現為增長較快，只有當循環荷載作用到一定次數后，隨著動應力的增大土樣發生破壞所需的循環振次N不斷減少，表現為很小的循環振次N范圍內就達到破壞，呈現脆性破壞特征。即存在一個臨界動應力比σd／2σc′。

當固結應力σc小于先期固結應力σv0情況下，＃1和＃2的臨界動應力比σd／2σc′分別為0.4和0.306；σc介于σv0和σvy之間時，＃1和＃2的σd／2σ′c分別為0.326和0.224；當σc大于σvy情況下，＃1和＃2的σd／2σc′分別為0.244和0.214。由此可見，結構性土體的臨界動應力比并不是一個定值，而是與圍壓大小相關的。

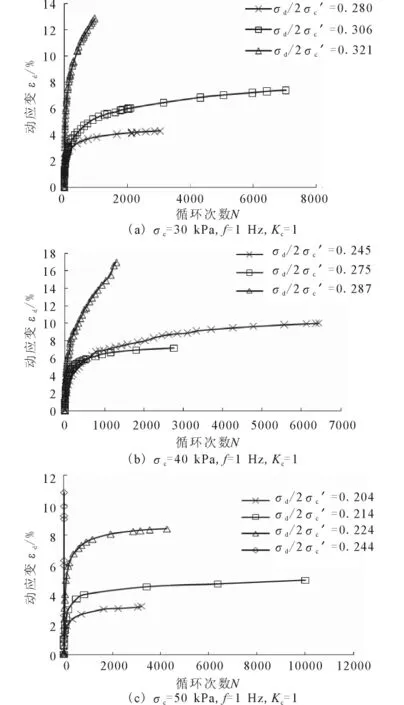
圖2 1號原狀土樣軸向動應變－循環振次關系曲線Fig.2 Relation curves of cyclic axial strain with cycle number of undisturbed clays＃1.

圖4為不同應力條件下軸向動應變－循環振次關系曲線。從圖中可以看出，當σc小于σv0情況下，變形轉折點對應的應變εd與σc介于σv0和σvy之間時所對應的應變值基本接近，然而，當σc大于σvy后，土樣發生破壞所需的循環振次N不斷減少，表現為很小的循環振次N范圍內就達到破壞，土樣的軸向動應變εd均表現為增長較快。

以上現象的產生可從土體的微觀結構角度出發給予解釋。由于土體結構性的存在，在低圍壓條件下，尤其是在低于土體的結構屈服應力情況下，土體的結構性基本上沒有遭到破壞，剛度較高，受到外力作用很難發生變形，所以達到破壞時所需要的循環應力比數值較大；而當應力水平超過結構屈服應力時，會出現結構性的大量破壞，土骨架剛度急劇變小，軸向應變則隨著振動次數的增加出現急劇增大現象，達到破壞所需要的循環應力比相應減小。

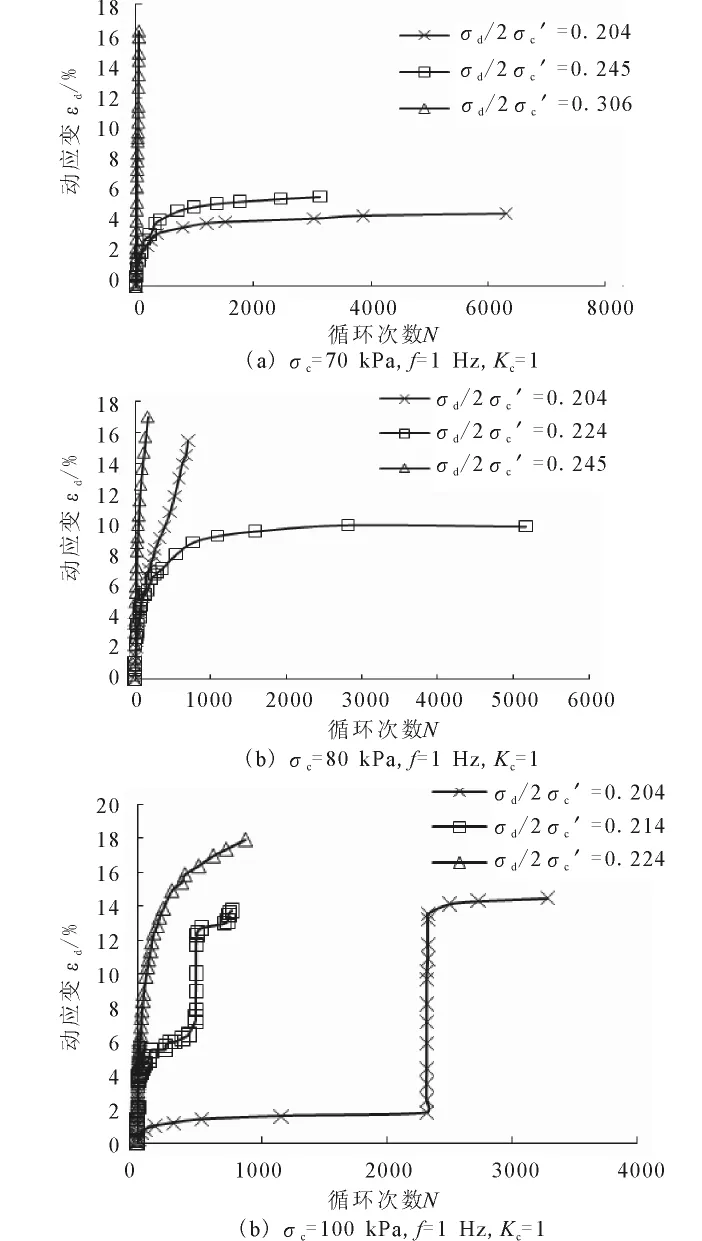
圖3 2號原狀土樣軸向動應變－循環振次關系曲線Fig.3 Relation curves of cyclic axial strain with cycle number of undisturbed clays＃2.

3.2 不同固結應力下的孔隙水壓力－循環振次關系

圖5為原狀軟土在不同固結壓力下的孔隙水壓力與振動次數之間的變化過程曲線。

從圖中可以發現：總的變化規律是隨著循環次數的增大孔隙水壓力不斷增大。當圍壓低于先期固結應力時，孔壓隨著振次的變化分兩種情況，一種是動應力比較小時，在最初的振次內孔壓隨著振次的增加而增加較快，當孔壓達到一定程度以后孔壓隨著循環振次的增加得非常緩慢，達到穩定狀態；另一種情況為動應力較大時，孔隙水壓力基本上隨著振

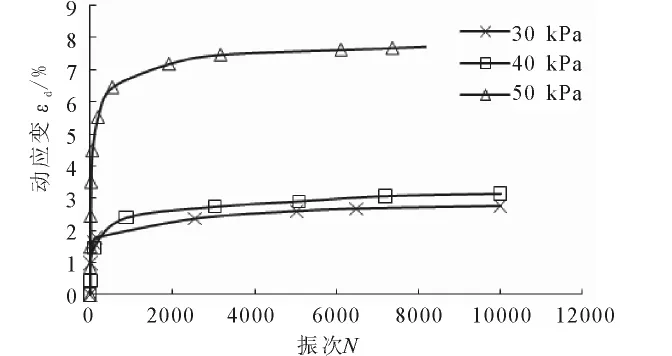
圖4 不同圍壓下應變－振次關系曲線Fig.4 Relation curves of cyclic axial strain with cycle number of the samples in different stress level.

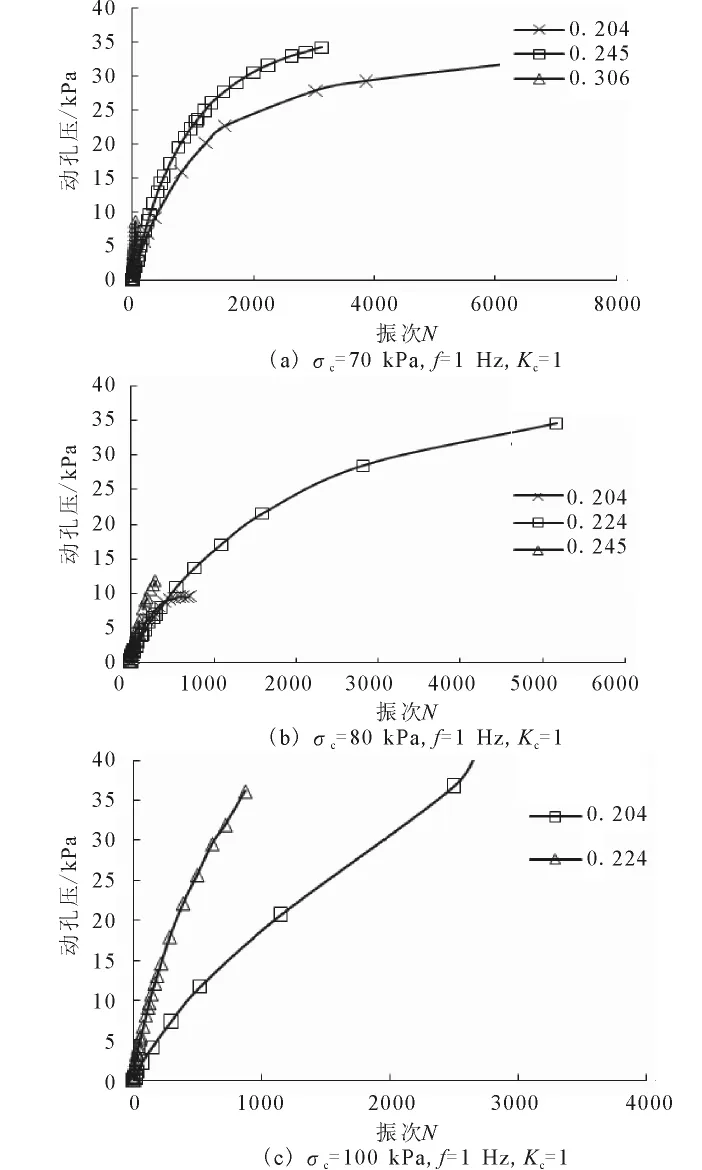
圖5 不同固結壓力下軸向動孔壓－振次關系曲線Fig 5 Relation curves of dynamic pore water pressure with cyclic number under different confining pressures.

次改變呈線性關系，并且增加的速率隨著動應力比的增大而增大。該臨界應力比和土體的軸向應變臨界循環應力比相同。

當圍壓超過先期固結壓力后，孔隙水壓力的變化基本上呈現出線性增長關系，同時動應力比的改變對于孔隙水壓力值的影響也趨于不明顯狀態。尤其是圍壓超過結構屈服應力后，這種現象更加明顯。其原因一方面是由于土體結構破壞，另一方面是試樣的滲透系數較小，從而使得孔隙水壓力在短期內不能得以消散，從而造成孔壓的線性增長。

3.3 不同固結應力下振動頻率的影響

圖6為不同固結應力下采用三種振動頻率得到的軸向動應變與振動次數的關系曲線。

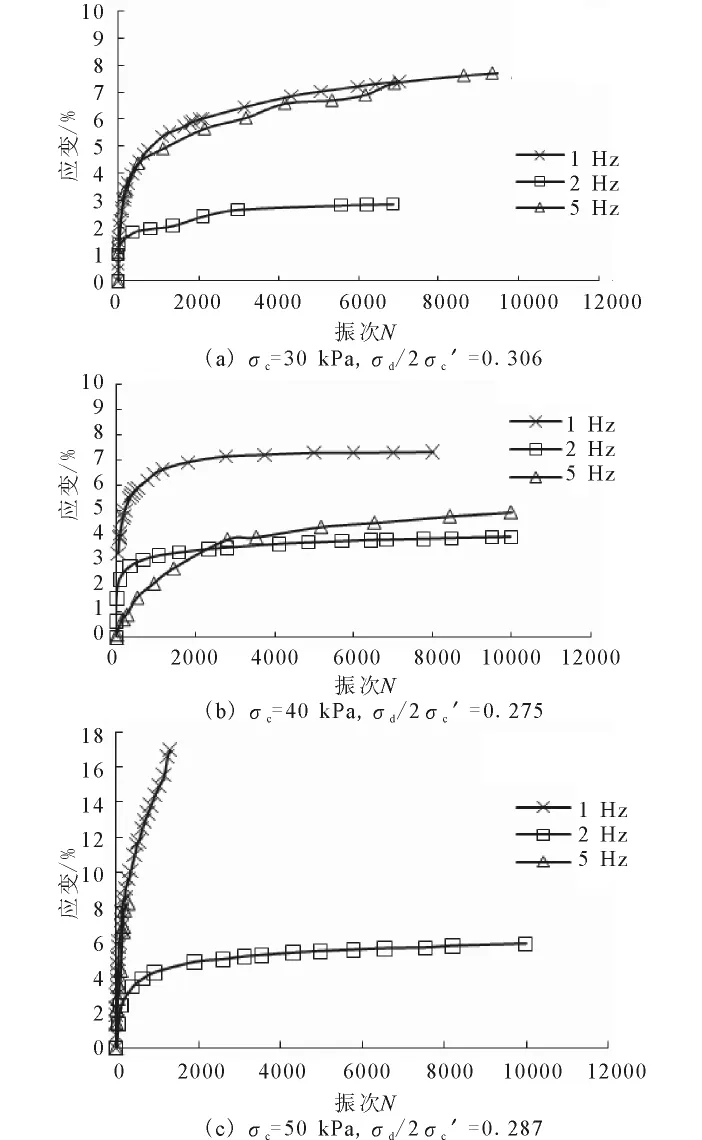
圖6 不同頻率下軸向動應變－振次關系曲線Fig 6 Relation curves of dynamic axial strain with cyclic number under different vibration frequencies.

從圖中可以看出，總的變化規律是無論固結應力的大小，均存在一個轉折頻率。當振動頻率低于或高于2Hz時，若圍壓低于結構屈服應力，軸向動應變隨著振次的變化表現為：在最初的振次內動應變隨著振次的增加增長較快，當動應變達到一定程度以后，隨著循環振次的增加增長得非常緩慢，達到穩定狀態；當圍壓高于結構屈服應力后，軸向動應變隨振次的變化基本上呈現出線性增長的關系。

振動頻率為2Hz時，軸向動應變與振次之間的關系曲線均表現為振次較少時動應變增長較快，之后，隨著振動次數逐漸增加動應變趨于穩定狀態，基本上不受固結應力大小的影響。

4 結論

本文以天津濱海新區典型結構性軟土為研究對象，通過一系列動三軸試驗，研究不同應力水平下結構性軟黏土的動力變形特性。據試驗結果可以得到以下一些結論：

（1）在動應變發展過程中存在一個臨界動應力比（σd／σc）t，該臨界動應力比并不是一個定值，而是與圍壓大小相關的，隨著圍壓的逐漸增大而降低。

（2）孔隙水壓力的變化以先期固結壓力和結構屈服應力為轉折點呈現出不同的變化規律：圍壓低于先期固結壓力時，孔壓隨著振次的變化分兩種情況；當圍壓超過先期固結壓力后，孔隙水壓力的變化基本上呈現出線性增長關系，同時動應力比的改變對于孔隙水壓力值的影響也趨于不明顯狀態；尤其是圍壓超過結構屈服應力后，這種現象更加明顯。

（3）無論固結應力為多少，均存在一個轉折頻率：當振動頻率低于或高于2Hz時，圍壓逐漸增大，軸向動應變隨著振次的變化從增加較快，之后趨于穩定狀態轉變為基本上呈現出線性增長關系；當振動頻率為2Hz時，固結應力的改變對軸向動應變的影響呈現不明顯狀態。

［1］Diylajee V A，Raymond G P.Repetive Load Deformation of Cohesionless Soil［J］.Geotech.Engrg.Div.，ASCE，1982，108（10）：1215－1229.

［2］Behzadi G，Yandell W O.Determination of elastic and plastic subgrade soil parameters for asphalt cracking and rutting prediction［J］.Transportation Research Record，1996，1540：97－104.

［3］王建榮，張振中，王峻，等.振動頻率對原狀黃土動本構關系的影響［J］.北地震學報，1999，21（3）：310－314.

［4］周建.循環荷載作用下飽和軟粘土的孔壓模型［J］.工程勘察，2000，（4）：7－9.

［5］鐘輝虹，黃茂松，吳世明，等.循環荷載作用下軟黏土變形特性研究［J］.土工程學報，2002，24（5）：629－632.

［6］Sakai A ，Samang L，Miura N.Partially－drained cyclic behavior and its application to the settlement of a low embankment road on silty－clay［J］.Soils and Foundations，2003，43（1）：33－46.

［7］顧中華，高廣運.循環荷載下飽和粘土強度等效計算探討［J］.西北地震學報，2005，27（1）：13－16.

［8］黃茂松，李進軍，李興照，等.飽和軟粘土的不排水循環累積變形特性［J］.巖土工程學報，2006，28（7）：891－895.

［9］沈珠江.軟土工程特性和軟土地基設計［J］.巖土工程學報，1998，20（1）：100－111.

［10］何開勝，沈珠江.天然沉積粘土的結構性調查［J］.東南大學學報（自然科學版），2002，32（5）：818－822.

［11］劉恩龍，沈珠江.不同應力路徑下結構性土的力學特性［J］.巖石力學與工程學報，2006，25（10）：2058－2064.

［12］郝玉龍，王立忠，陳云敏，等.深厚軟土水泥攪拌樁復合地基沉降分析及控制［J］.巖土工程學報，2001，23（3）：345－349.