基于灰色層次分析法的高校崗位津貼設計模型

肖亞奇

(通化師范學院 人事處,吉林 通化 134002)

高校崗位津貼制度是高校在上級主管部門核定的績效工資總量內，按照規范的分配程序和要求，自行制定實施的靈活多樣的薪酬分配辦法；它不受政府財政撥款的保障，經費自理.所以高校崗位津貼既受上級主管部門核定的績效工資總量限制，又受高校財務狀況的制約.但隨著國家收入分配改革的進行，它將作為國家工資制度的補充和完善部分，在一定時間內將替代績效工資在高校起著激勵作用.本文將利用灰色層次分析法[1]在高校有限的財力下，根據學校發展定位科學確定不同崗位等級的津貼標準，充分發揮高校崗位津貼的激勵作用.

1 灰色層次分析法

A.L.Saaty提出的AHP[2]是用一個實數來描述進行比較的兩元素的相對重要程度，而在實際的操作過程中，兩元素之間的相對重要程度往往難以用確定的數值來衡量.這時，考慮用灰數來代替實數進行衡量，建立灰色層次分析法，其步驟與AHP基本一致.

1.1 灰色判斷矩陣的建立

灰色判斷矩陣?(R)表示針對上一層某元素，本層次與之有關元素之間相對重要程度的比較，假定上一層次的元素C同下一層次中的元素a1,a2,…,an相關聯，則灰色判斷矩陣可表示為：

Ca1a2…ana1(r11)(r12)…(r1n)a2(r21)(r22)…(r2n)……………an(rn1)(rn2)…(rnn)

元素?(rij)表示元素ai和元素aj相對于元素C進行比較時，元素ai比元素aj重要程度的灰數標度，為了得到定量描述，約定如表1.

表1 灰數判斷標度

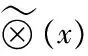
有了上面的判斷標度后，灰色判斷矩陣

具有如下性質：

(1)?(rii)=1,i=1,2,…,n.

1.2 權重系數和最大特征根的數值求解

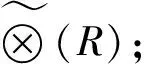
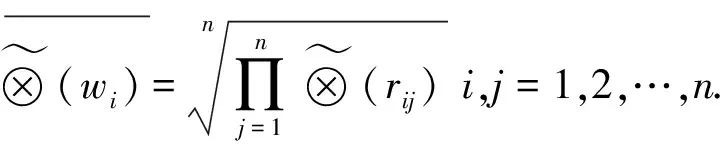
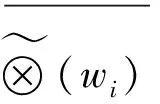
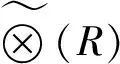
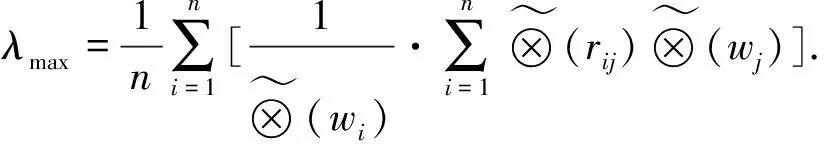
1.3 一致性檢驗

對灰色判斷矩陣的一致性檢驗的步驟如下：

(2)查找相應的平均隨機一致性指標RI.對n=1,…,9,Saaty給出了RI的值，見表2.

表2 RI值

當CR<0.10時，認為判斷矩陣的一致性是可以接受的，否則應對判斷矩陣適當修正.

1.4 層次總排序及一致性檢驗

上面我們得到的是一組元素對其上一層中某元素的權重向量.我們最終要得到最低層中各方案對于目標的排序權重.總排序權重要自上而下地將單準則下的權重進行合成.

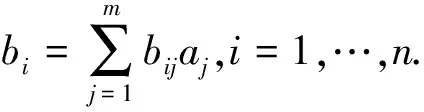
對層次總排序也需作一致性檢驗，檢驗仍象層次總排序那樣由高層到低層逐層進行.這是因為雖然各層次均已經過層次單排序的一致性檢驗，各成對比較判斷矩陣都已具有較為滿意的一致性.但當綜合考察時，各層次的非一致性仍有可能積累起來，引起最終分析結果較嚴重的非一致性.

設B層中與Aj相關的因素的成對比較判斷矩陣在單排序中經一致性檢驗，求得單排序一致性指標為CI(j)，(j=1,…,m)，相應的平均隨機一致性指標為RI(j)(CI(j)、RI(j)已在層次單排序時求得)，則B層總排序隨機一致性比例為

當CR<0.10時，認為層次總排序結果具有較滿意的一致性并接受該分析結果.

2 應用

某教學型高校要對教授、副教授、講師、助教四個崗位類別進行崗位津貼標準設計，根據學校財務狀況，要求崗位津貼標準總和不超過4000元.現將教學、科研、師德、社會服務[3]作為評判標準，層次結構模型如圖1.

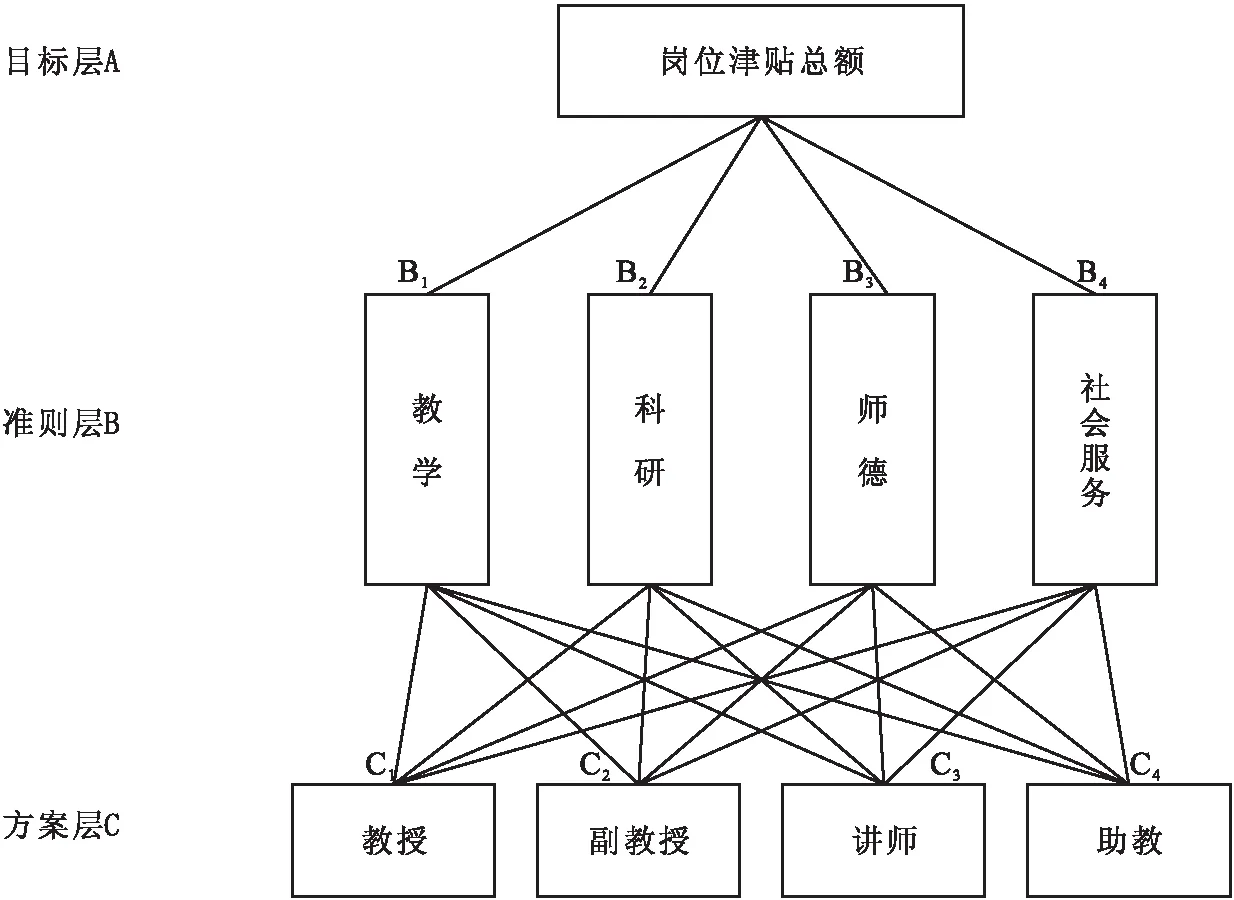
圖1 層次結構圖

某評判人給出如下灰色判斷矩陣：

AB1B2B3B4B1(1)(2)(5)(5)B2(12)(1)(3)(1)B3(15)(13)(1)(1)B4(15)(1)(1)(1)

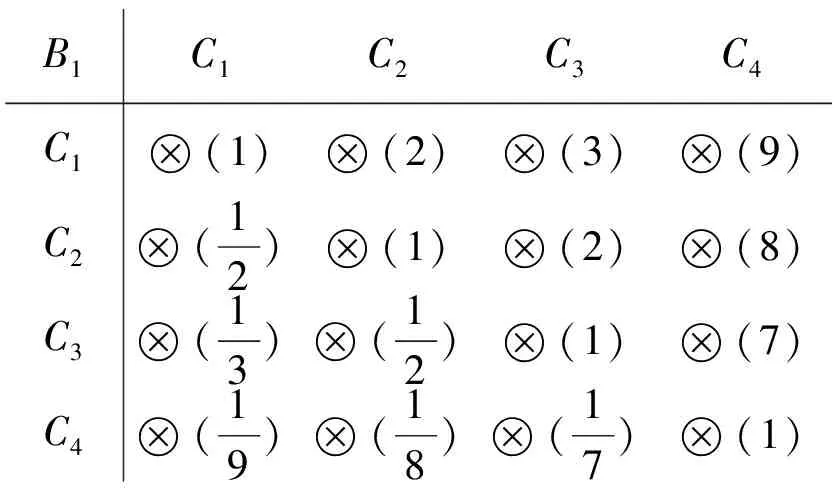
B1C1C2C3C4C1(1)(2)(3)(9)C2(12)(1)(2)(8)C3(13)(12)(1)(7)C4(19)(18)(17)(1)

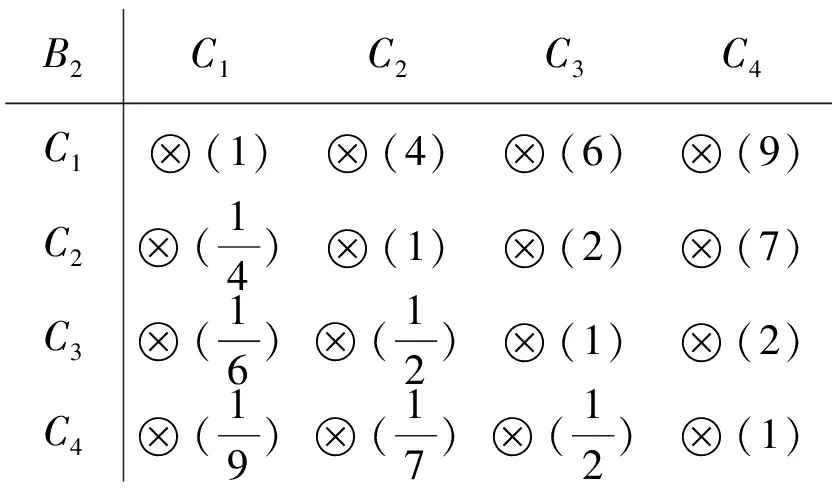
B2C1C2C3C4C1(1)(4)(6)(9)C2(14)(1)(2)(7)C3(16)(12)(1)(2)C4(19)(17)(12)(1)

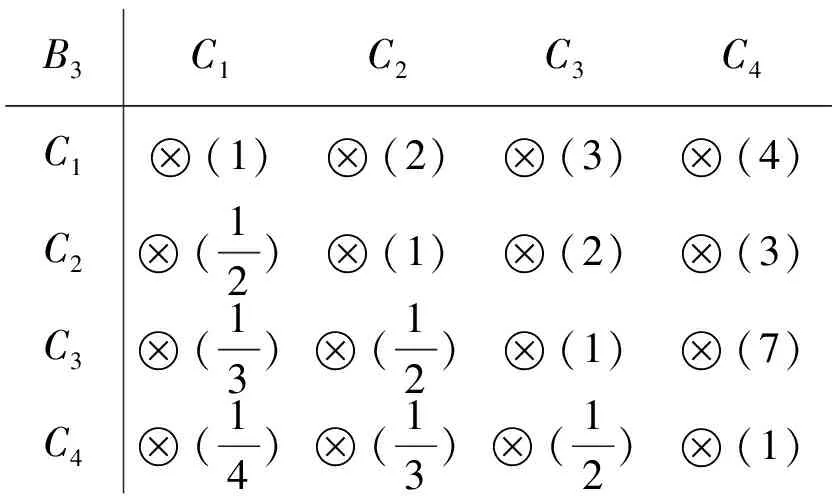
B3C1C2C3C4C1(1)(2)(3)(4)C2(12)(1)(2)(3)C3(13)(12)(1)(7)C4(14)(13)(12)(1)

B4C1C2C3C4C1(1)(6)(8)(9)C2(16)(1)(3)(4)C3(18)(13)(1)(2)C4(19)(14)(12)(1)

根據灰色層次分析法計算步驟，計算結果見表3.

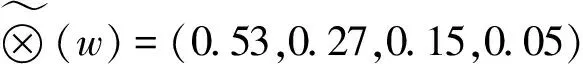
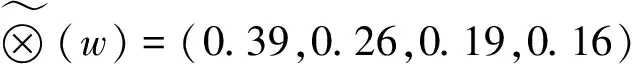
3 總結

本文應用灰色層次分析法對崗位津貼標準進行了設計，設計結果全面、客觀、公正地反映了評判人的想法，信度、效度較高，設計結果易讓全體教師接受，此設計方案能充分發揮高校崗位津貼的激勵作用.

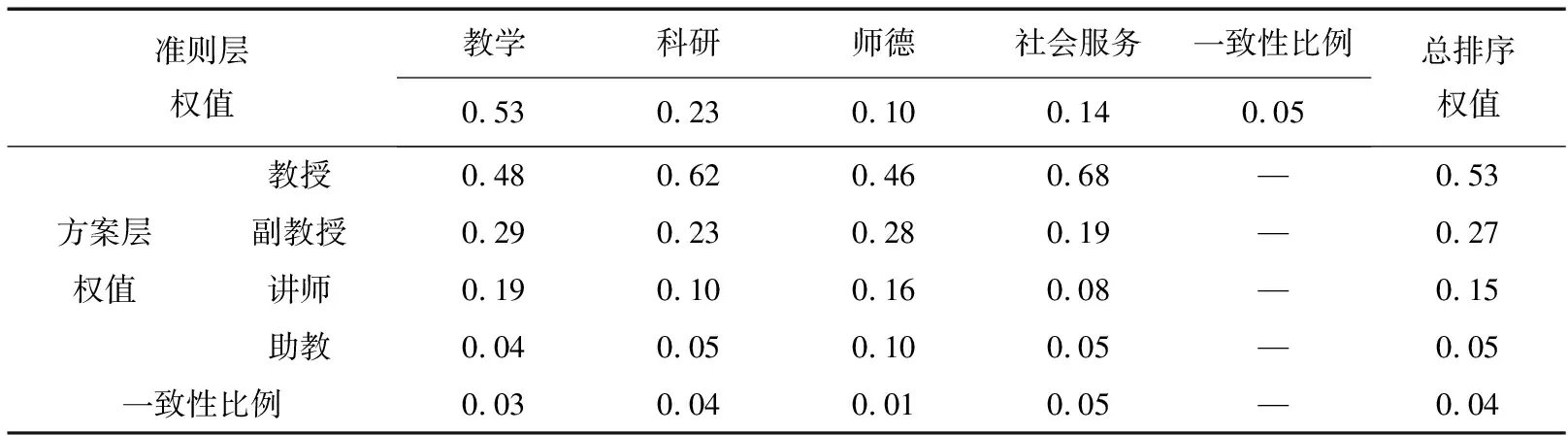
表3 灰色層次分析法計算結果

[1]鄧聚龍.灰色系統基本方法[M].武漢:華中理工大學出版社,1987.

[2]楊娜.基于層次分析法的人力資源評價[J].中國管理信息化,2007,10(10).

[3]李黎.對高校教師績效工資考核標準的探析[J].經濟師,2009(11).