風帆輔助推進船舶操縱可控區研究

陳紀軍，吳寶山，沈定安

（中國船舶科學研究中心，江蘇 無錫 214082）

風帆輔助推進船舶操縱可控區研究

陳紀軍，吳寶山，沈定安

（中國船舶科學研究中心，江蘇 無錫 214082）

加裝風帆后的船舶在低速時的航行特性有別于無帆情形。為確保低速航行安全，基于MMG非線性運動方程，計算了有、無風帆情況下的船舶操縱可控區。運動方程中的船體水動力系數、舵模塊參數等由經驗公式得到，帆/船整體氣動力系數由基于滑移網格方法的CFD手段獲得。計算結果表明：不同帆攻角下的船舶自由操控區不同，通過合理的帆/舵聯合操縱，可以擴大風帆輔助推進船舶低速航行的可自由操控區，增強其在風中的抗風能力。

風帆；滑移網格；自由操控區；風速限界線；非線性

1 引 言

近年來，隨著全球能源日趨短缺，油氣價格飛速攀升，如何降低燃料成本逐漸成為眾多行業關注的焦點；此外燃燒這些石化燃料排放的氣體也給環境帶來嚴重影響（CO2使得全球氣候變暖，NOX、SOX造成酸雨等），因此如何減少污染物排放成為關注的另外一大焦點。船舶運輸業作為一大能源消耗產業，近年來隨著航運量的飛速增長，給環境帶來的影響也已不容忽略，鑒于此，一些世界性的組織如國際海事組織（IMO）、歐盟（EN）等，相繼頒布了各種國際公約與規則，如國際船舶能效設計指數（EEDI）新規約，加強對船舶設計、生產、營運等的嚴格監控。在此背景下，船舶運營商們不斷地去尋求各種高效的節能減排方式，風帆輔助船舶推進技術就是其中一項重要技術。

明顯地，加裝風帆將會使得船舶原有的受力特性發生改變，這也必然直接導致船舶操縱特性的改變。考慮到船舶低速航行時，舵效較低，因此為確保風帆輔助推進船舶低速航行時的安全，有必要分析加裝風帆對于船舶低速航行時的抗風能力影響變化，也即確定船舶的可自由操控區及使得操縱性喪失的極限風速。

關于風對船舶航行性能影響研究最早可以追溯至1933年[1]，其后比較有代表性的是Eda[2]，他研究了風對船舶航向穩定性的影響；Ogawa首次研究了風中船舶的回轉性[3]。縱觀早期操縱性研究，大都有一個顯著的缺點，即數學模型中采用的是線性水動力系數，從本質上講，這只是在小的漂角及小的艏搖角速度下有效。然而，船實際在風中低速前進時，漂角可能很大，因此為準確評估船在風中低速航行時的抗風能力，有必要考慮高階的水動力系數。上世紀八十年代后，伴隨著計算機及測試水平的發展，Martin（1980）[4]、夏尚鈺[5]、沈定安[6]、馬向能[7]等對風中的船舶操縱性各類問題進行了計算與試驗的對比，對船舶的保向性能進行了分析，并給出了船舶航行時的臨界風速。關于風帆輔助推進船舶的舵力保向研究，目前公開發表文獻甚少[8]。

為評估加裝風帆對于風帆輔助推進船舶低速航行時的抗風能力影響，本文基于MMG非線性運動方程組，計算了有、無風帆情況下的船舶在滿載情況下不同舵角時的風速限界線，通過對比分析，確定了不同相對風向角下的最優操帆角，為風帆輔助推進船舶的安全低速航行提供了操縱策略。運動方程中的船體水動力系數、舵模塊參數等由經驗公式擬合得到，帆/船整體氣動力系數由基于滑移網格方法的CFD手段獲得。

2 風帆輔助推進船舶運動坐標系定義

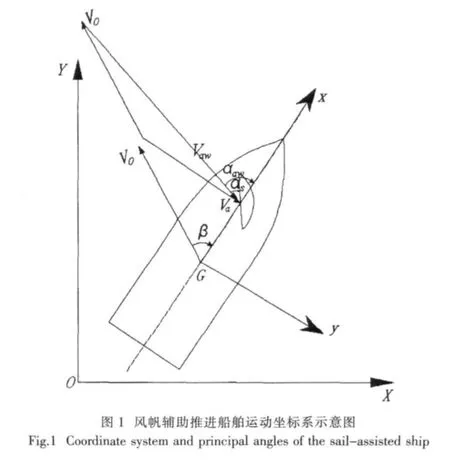
定義大地坐標系O-XYZ和船體坐標系G-xyz，如圖1所示。其中船體坐標系G-xyz原點選在船體重心G處，x軸指向船艏，y軸指向船右舷，Gz軸垂直于Gxy平面，其正向使G-xyz構成右手直角坐標系。此外，船實際航速V0與Gx正向之間的夾角稱為漂角β，規定V0轉向Gx軸順時針方向為正；實際風速記為Va，根據速度三角形關系，在風帆安裝處實際感受到的是風速Vaw，此為相對風速，其與船艏間的夾角稱為相對風向角，記為βaw，與風帆弦向之間的夾角稱為帆攻角，記為αs，并且定義帆面迎流前緣向右偏轉為帆攻角αs的正方向。

3 數學模型

為了方便計算風帆輔助推進船舶的風速限界線，確定可自由操控區，引入如下假定：

（1）作用在風帆輔助推進船舶上的為均勻風，并且不考慮由之引起的自由面興波效應；

（2）船體水動力系數不隨航速的變化而改變；

（3）不考慮船合速度的變化以及定常均勻風作用下風帆輔助推進船舶的橫傾與縱傾改變。

在上述假定下，按照準定常處理，風帆輔助推進船舶在風中操舵保向時滿足側向力Y和偏航力矩N平衡，船體所受各流體動力之間滿足下述關系：

式中，腳標“H”代表船體水動力（矩）項，腳標“R”代表舵力（矩）項，腳標“a”代表船體氣動力（矩）項，當加帆時，代表帆/船整體氣動力（矩）。考慮到風帆輔助推進船舶在低速航行時，為克服風作用于船體上的氣動力，船需要保持的橫向速度可能會比較大，所以在船體力中計及水動力系數的非線性項。具體地，船體側向力Y及偏航力矩N按照如下形式表達：

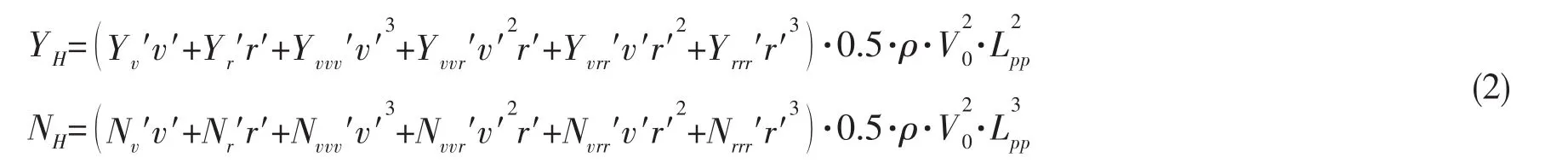
上式中，各船體水動力系數由文獻[9]中的經驗公式結合目標船的相關參數獲得；式中的舵力（矩）表達成：

式中，aH為舵對船體水動力的影響系數，xR為舵中心到船重心的縱向距離，這里取xR=0.5Lpp，xH為操舵誘導船體橫向力作用中心到船舶重心的距離，可由下式計算[10]：

式中，AR為側向投影面積，fA為舵的升力系數在攻角為0時的斜率，是展弦比Λ的函數，記為：

式中，Λ可表述為Λ=H2/AR，H為舵高。

風帆輔助推進船舶所受氣動力可表述為：

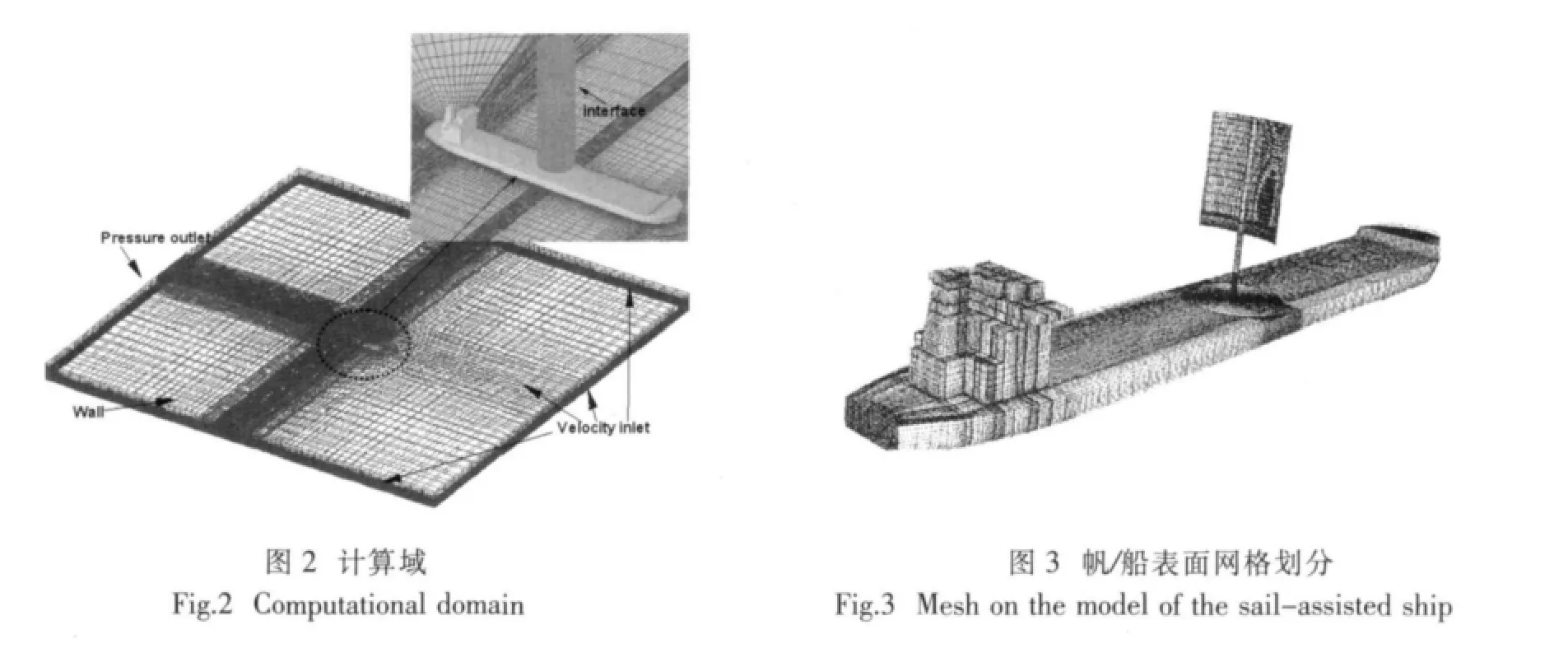
上式中，ρa為空氣密度，Vaw為相對風速，Cya，Cna為帆/船整體氣動力（矩）系數，是相對風向角 βaw、帆攻角αs的函數，由基于CFD的滑移網格方法（圖2、3）預報得到，關于計算方法的驗證及結果參見文獻[11-12]。

4 風帆輔助推進船舶操縱可控區計算

4.1 計算對象

本文計算對象為一艘加裝圓弧形風帆的76000噸散貨船，表1～3中列出目標船、舵、帆的主參數。

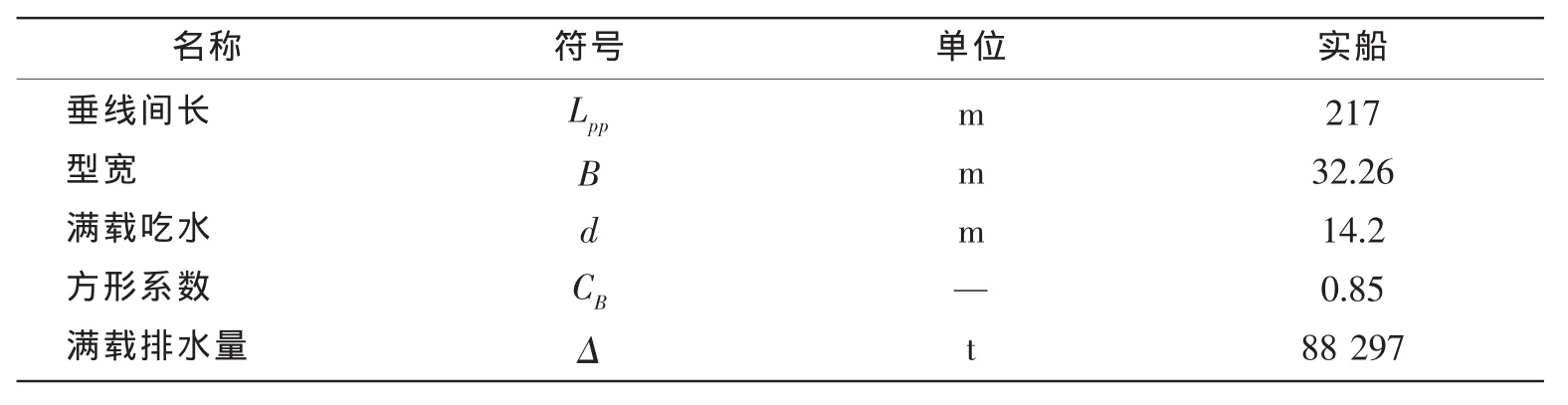
表1 散貨船主參數Tab.1 Main parameters of the bulk carrier

表2 舵主參數Tab.2 Main parameters of the rudder

表3 圓弧形風帆主參數Tab.3 Main parameters of the arc-sail

4.2 計算工況說明

（1） 計算散貨船無帆情況時，不同舵角（+35°、+25°、+15°、+5°）下的風速限界線，并與文獻[4]進行對比，初步驗證本文數學模型的可靠性；

（2） 計算散貨船不同帆攻角時，在不同舵角（+35°、+25°、+15°、+5°）下的風速限界線，帆攻角 αs∈［0°,180 ］° ，Δαs=20°。

4.3 風帆輔助推進船舶風速可控區的計算與分析

4.3.1 數學模型的驗證

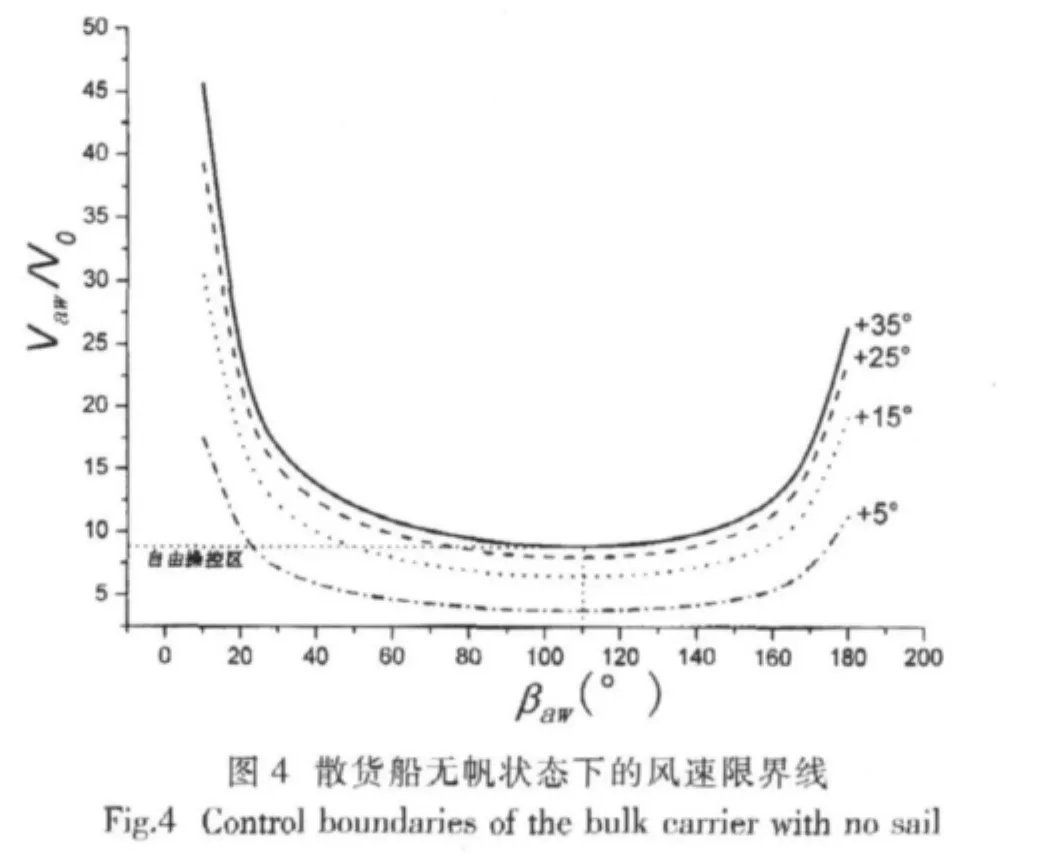
散貨船無帆情況下不同舵角時的風速限界線計算結果參見圖4所示。由圖4可知，隨著舵角的增大，在某一相對風向角下所能承受的最大相對風速變大，在整個相對風向角范圍內可自由操縱區的上限（ Vaw/V0）max≈8.4；此外，通過與文獻[4]的比較，兩者曲線形狀相似，定性地驗證了本文數學模型的可靠性。

4.3.2 不同帆攻角情況下的風速限界線隨舵角變化規律

在驗證數學模型可靠性的基礎上，探討了不同帆攻角情況下風帆輔助推進船舶的風速限界線。計算結果參見圖5所示。

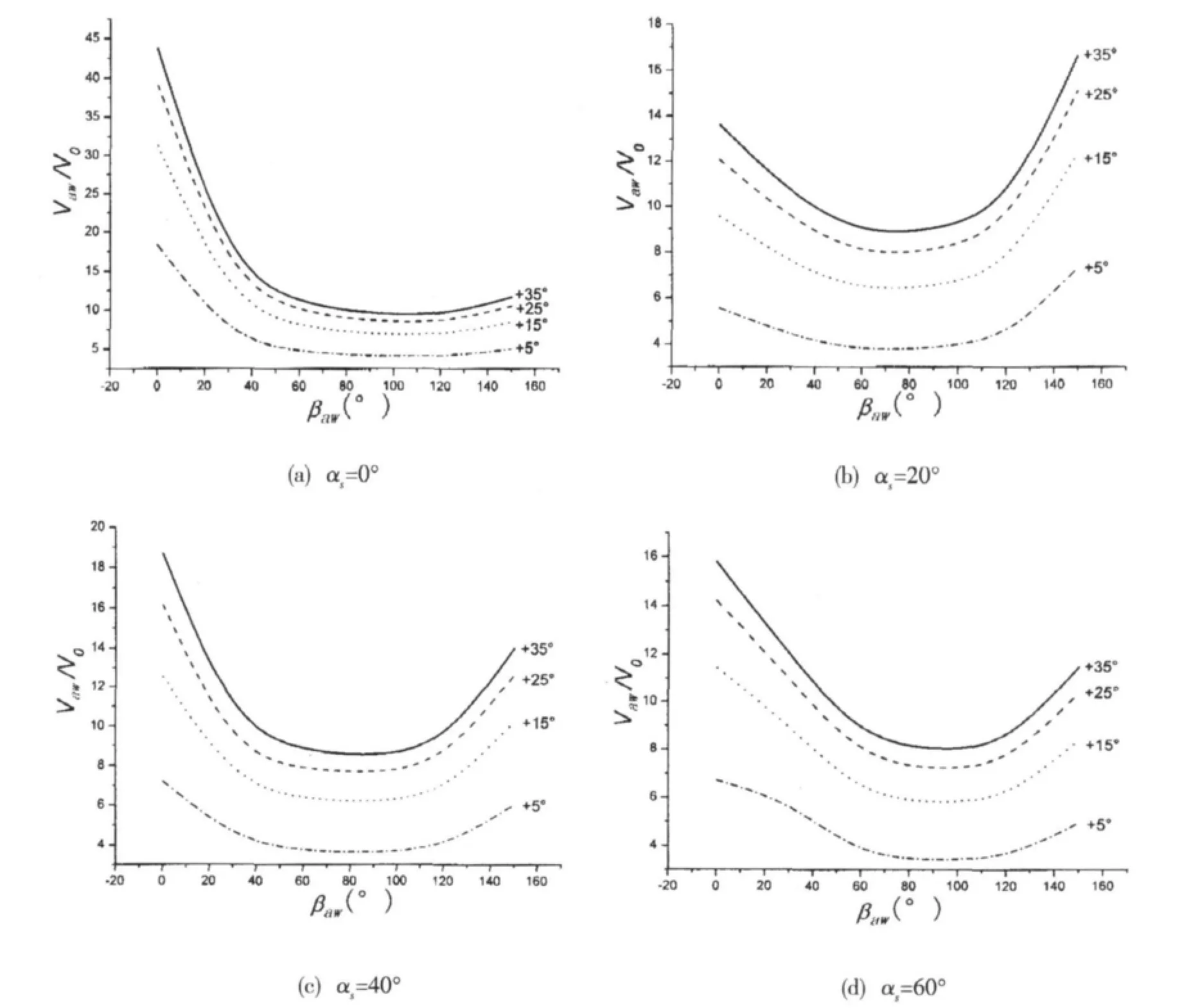
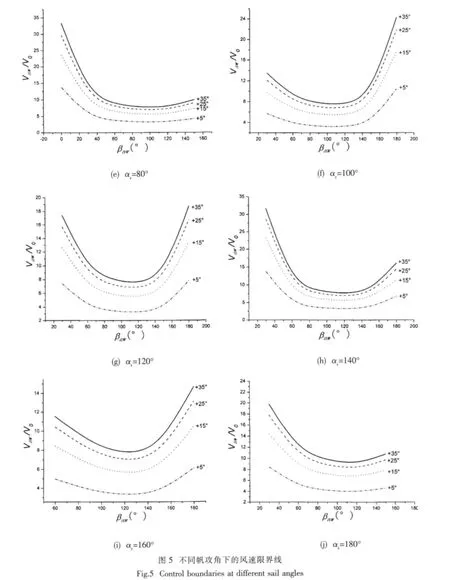
由圖5可見，風帆輔助推進船舶在不同帆攻角下的可自由操控區有相當大的區別，倘若在不同相對風向角下通過適當合理地操帆可以顯著擴大可自由操控區。通過對系列帆攻角下的數據分析，整理獲得不同相對風向角下的最優操帆，具體操帆角隨相對風向角變化關系列于表4中。

由之獲得的最優操帆與無帆時的風速限界線對比參見圖6所示。

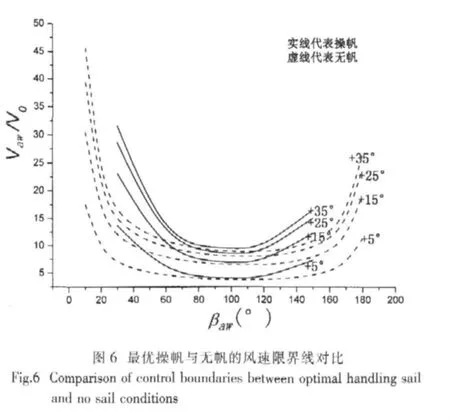
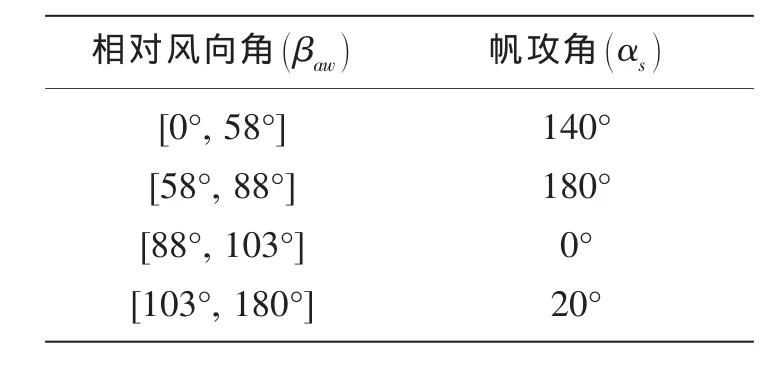
表4 風帆輔助推進船舶低速航行時的最優操帆策略Tab.4 Handling strategies for a sailassisted ship at low speed

由圖6可見，通過合理操帆，可自由操縱范圍的上限 （Vaw/V0）max≈9.3，有效提高了風帆輔助推進船舶的可自由操縱范圍。

5 結 論

（1）基于MMG非線性運動方程組，獲得了有無風帆情況下的散貨船風速限界線，通過計算表明，不同相對風向角下操帆角不同，抗風能力不同。在此基礎上，通過數據分析，獲得了達到最大可自由操縱范圍上限時的最優操帆策略，與無帆情況相比，顯著增大了可自由操縱區。本文工作，可為深入開展風環境下加裝多帆后的散貨船操縱性預報及仿真奠定基礎；

（2）本文并未考慮風/浪聯合作用，因此在后續工作中，需深入開展這方面的研究。

[1]Hughes G.The effect of wind on ship performance[J].Trans.INA,1933.

[2]Eda H.Low-speed controllability of ships in a wind[J].Journal of Ship Research,1968,12(3):181-200.

[3]Ogawa A.Calculation of the steered motion of ships under the action of external forces.Part I.Course keeping and turning of a ship in uniform wind and flow[J].Journal of the Society of Naval Architects of Japan,1969,126.

[4]Martin L L.Ship maneuvering and control in wind[J].SNAME Transactions,1980,88:257-281.

[5]夏尚鈺,竺瑞庭.均勻風作用下的船舶操縱性研究[J].艦船科學技術,1984,10:1-14.

[6]馬向能,沈定安,何春榮.大型集裝箱船受風工況下操縱性計算預報[J].船舶力學,2001,5(4):17-28.

[7]沈定安,馬向能.船隊風浪中操縱可控區的計算[J].船舶力學,2008,12(4):582-587.

[8]湯 躍,吳秀恒.風帆助航船操縱性研究[J].中國造船,1986,3:8-19.

[9]孫澄溥.肥大型船操縱性船體水動力導數的經驗估算方法（深水部分）[R].無錫:中國船舶科學研究中心科技報告,1995.

[10]賈欣樂,楊鹽生.船舶運動數學模型-機理建模與辨識建模[M].第一版.大連:大連海事大學出版社,1999.

[11]陳紀軍.風帆輔助推進船舶氣動力特性數值研究[R].無錫:中國船舶科學研究中心科技報告,2010.

[12]陳紀軍.風帆輔助推進船舶氣動力數據庫的建立[R].無錫:中國船舶科學研究中心科技報告,2010.

Freely maneuverable range study for a sail-assisted ship

CHEN Ji-jun,WU Bao-shan,SHEN Ding-an
(China Ship Scientific Research Center,Wuxi 214082,China)

Ship’s sailing performance will be changed when sails are installed.In order to sail safely at slow speed,freely maneuverable range for a sail-assisted ship was presented under both with and no sail conditions based on the MMG nonlinear motion equations.Hull hydrodynamic coefficients and rudder module parameters were calculated by empirical formula,and wind force coefficients of sail/hull were predicted by CFD based on the sliding meshes.The result showed that freely maneuverable range varies with sail angles,and freely maneuverable range for a sail-assisted ship at slow speed can be enlarged through reasonably handling sail and rudder.

sail;sliding mesh;freely maneuverable range;control boundaries;nonlinear

U661.3

A

1007-7294（2011）05-0456-07

2010-11-03

陳紀軍（1984-），男，中國船舶科學研究中心碩士生；吳寶山（1968-），男，研究員。