船舶上層建筑整體縱向振動固有頻率預報方法研究

殷玉梅，趙德有

（大連理工大學 船舶工程系，遼寧 大連 116085）

船舶上層建筑整體縱向振動固有頻率預報方法研究

殷玉梅，趙德有

（大連理工大學 船舶工程系，遼寧 大連 116085）

文章推導了船舶上層建筑整體縱向振動固有頻率預報公式，將上層建筑整體縱向振動固有頻率視為由上層建筑根部剛性固定在主船體上的剪彎振動固有頻率和上層建筑根部彈性固定在主船體上的剛體回轉振動固有頻率兩部分串聯合成，重點研究了上層建筑剛體回轉振動固有頻率計算公式中等效剛性系數的取法，并對剪切振動固有頻率計算公式進行了修正，給出了考慮彎曲振動影響的修正系數計算公式。采用三維有限元模型計算了6600TEU集裝箱船、112000t油輪、35000t散貨船、PANAMAX型油船、31000t散貨船和12000t貨船六條船的上層建筑整體縱向振動固有頻率以及剪彎振動固有頻率和剛體回轉振動固有頻率，并且得到了各條船的等效剛性系數，繪制了等效剛性系數曲線。以52000t大艙口貨船為例，采用本文方法計算其上層建筑整體縱向振動固有頻率，與實測值較為接近，證明文中提出的方法是可行的。

上層建筑；固有頻率；等效剛性系數；彎曲振動修正系數

1 引 言

1.1 研究概況

船舶上層建筑是船員休息的場所，屬于臥室區和生活區，同時也是精密儀器安裝較多的場所，該區域對振動水平要求較高。船舶上層建筑出現嚴重的振動將直接影響船員的生活以及儀器設備的正常使用，因此上層建筑的振動問題一直受到國內外學者的普遍重視。現代船舶采用機艙和上層建筑布置在艉部的形式日益增多，使上層建筑接近螺旋槳和主機這兩個船上的主要振源，導致上層建筑經常處于較大的激勵作用下。同時為了改善駕駛視線的需要以及船員人數的減小，往往將上層建筑設計得更高、更短；為了減小噪聲，采用上層建筑和機艙棚、煙囪分離型式，這樣就使上層建筑整體剛度有所減弱，導致上層建筑整體振動固有頻率降低，易與螺旋槳葉頻和主機高階激勵頻率相遇，產生共振并造成有害振動。目前國內外建造的船舶，上層建筑經常發生劇烈振動現象，為了解決上層建筑振動問題，關鍵是在船舶設計階段能較準確地預報出上層建筑固有頻率。這樣就可從避免上層建筑共振的角度合理地選擇主機型號和螺旋槳葉數；或者當主機型號、螺旋槳葉數已確定時，可以通過改變上層建筑尺度和構件尺寸等方式來改變其固有頻率，避免發生上層建筑共振。否則如果在船舶建造完成后發現上層建筑整體振動問題再去解決，將會造成人力、物力的巨大浪費。

上層建筑振動包括上層建筑整體振動和局部振動，其中上層建筑整體振動是指上層建筑整體縱向振動、橫向振動和扭轉振動。上層建筑整體縱向振動最常見也是人們最關心的問題。對于上層建筑整體縱向振動計算，目前有兩種方法：經驗公式法和有限元法。在上層建筑整體縱向振動研究方面，國內外很多學者已經做了大量工作，大沼覺等[1]提出了上層建筑根部固定時剪切振動固有頻率計算公式。馬廣宗等[2]運用正交試驗、回歸分析等方法提出了上層建筑縱向振動固有頻率公式。曹迪等[3]運用統計回歸和力學分析相結合的方法提出了上層建筑縱向振動固有頻率公式。趙德有等[4]提出一種計算上層建筑基礎的剛性系數和上層建筑剛體回轉振動固有頻率的算法，并利用文獻[1]提出的剪切振動固有頻率計算公式，得到了船舶上層建筑縱向振動固有頻率公式。此外，許多船級社[5-6]也給出了上層建筑整體縱向振動固有頻率的近似計算公式。近年來隨著計算機技術的發展，許多學者[7-9]采用三維有限元方法研究船舶上層建筑的動力特性，三維有限元模型是一種接近船舶真實結構的計算模型，能夠較準確地計算船舶振動特性，但三維有限元方法的計算模型復雜，計算工作量大，不適合在船舶設計初期使用。

1.2 近似公式與三維有限元法計算結果比較

本文利用日本海事協會（NK）、挪威船級社（DNV）、英國勞氏船級社（LR）、法國船級社（BV）和英國船舶研究協會（B.S.R.A）所提出的經驗公式以及三井造船公司、富田法和文獻[3]中方法分別計算了12000t貨船、6600TEU集裝箱船、112000t油輪、PANAMAX型油船、31000t散貨船和35000t散貨船的上層建筑整體縱向振動固有頻率，并與三維有限元方法的計算結果進行了比較，計算結果見表1。由表1中的計算結果可知，各種經驗公式的計算結果之間存在較大差異，這是由于上述經驗公式中有的方法考慮的影響因素較少，有的沒有完全體現出上層建筑整體剛度和質量分布影響，有的雖然考慮了上層建筑整體剛度和質量分布影響，但未能充分考慮上層建筑整體與主船體之間連接的剛度，而且有的經驗公式需要根據相關參數查圖求得固有頻率，這又引入了一定的人為誤差。并且現有的經驗公式無法準確地考慮主船體對上層建筑振動特性的耦合影響。因此更精確地預報上層建筑整體縱向振動固有頻率具有重要的理論意義和工程實用價值。

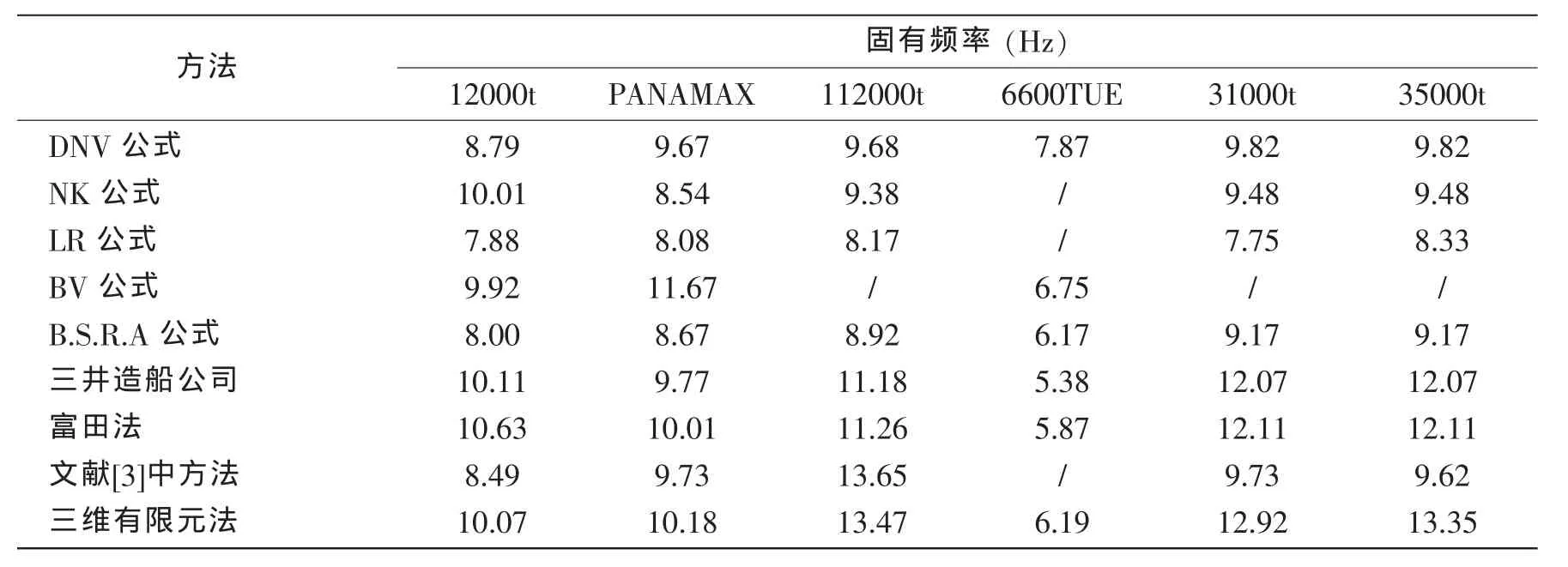
表1 上層建筑整體縱向振動固有頻率計算結果Tab.1 Natural frequency of superstructure’s overall longitudinal vibration

2 上層建筑整體縱向振動固有頻率公式推導

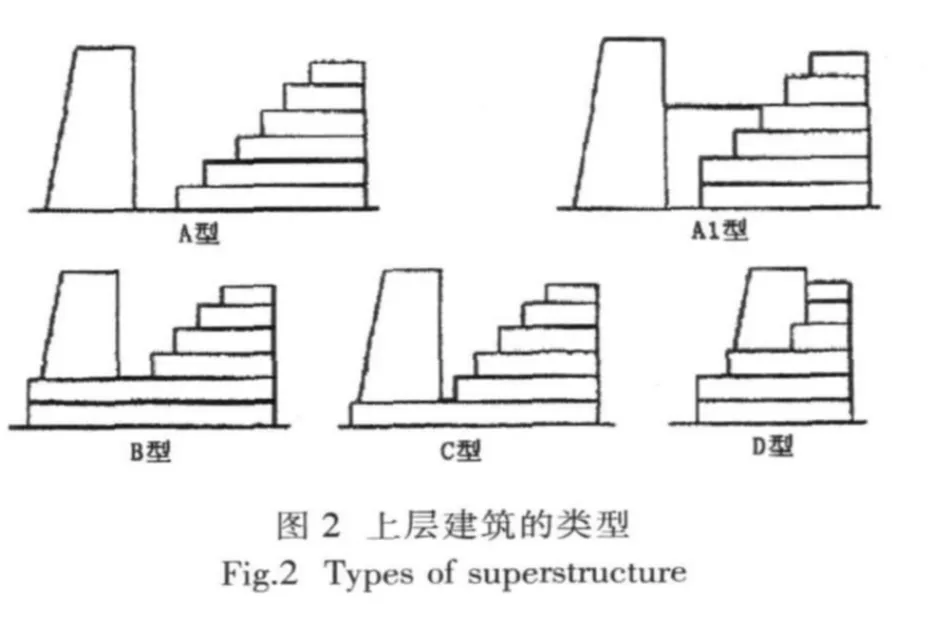
由國內外學者多年的理論研究和試驗研究可知，影響上層建筑整體縱向振動固有頻率的主要因素是上層建筑的剪切和彎曲剛度及其分布、上層建筑質量及其分布以及上層建筑根部與主船體的連接剛度。目前國內外用于船舶上層建筑整體縱向振動固有頻率計算的近似算法大致可分為兩類：其中一類方法只考慮上層建筑的主要尺度（總高度、各層高度和長度）、層數和上層建筑類型等參數，根據上層建筑整體縱向振動固有頻率實測值采用回歸方法獲得估算公式；另一類方法是將上層建筑整體縱向振動固有頻率視為由上層建筑根部剛性固定在主船體上的剪彎振動固有頻率和上層建筑根部彈性固定在主船體上的剛體回轉振動固有頻率兩部分組成，采用簡單串聯公式計算上層建筑整體縱向振動固有頻率，即按下式計算：

式中：fc為上層建筑整體縱向振動固有頻率，Hz；fs為上層建筑根部固定時縱向剪彎振動固有頻率，Hz；fr為上層建筑根部為彈性支持時剛體回轉振動固有頻率，Hz。

2.1 剪彎振動固有頻率

文獻[1]中，上層建筑根部固定時，上層建筑整體僅作剪切振動，其固有頻率按（2）式計算：

式中：fJ′為上層建筑根部固定時剪切振動固有頻率，Hz；H為艉樓甲板以上的上層建筑總高度，m；n為艉樓甲板以上的上層建筑總層數；i為上層建筑由下而上的層數；Mi為第i層上層建筑質量，kg，除圖2中A類型上層建筑外，其它類型上層建筑的質量應計入煙囪質量；φi為第 i層質量系數，按公式（3）計算；Si為第i層剪切面積，m2；G為材料的剪切模量，N/m2。

由于文獻[1]在推導中只考慮了上層建筑的剪切振動，沒有考慮上層建筑的彎曲振動，這與上層建筑整體縱向振動的實際情況不符，使計算結果偏高，因 此需要對其進行修正。本文給出了以剪切為主的剪彎振動固有頻率計算公式：

其中C為考慮彎曲振動影響的修正系數。

彎曲振動修正系數C的推導過程如下：本文將彎曲振動修正系數取為一階剪彎振動固有頻率與一階剪切振動固有頻率之比。

梁的彎曲振動方程：

式中：I為梁元截面慣性矩，m4；E為材料的彈性模量，N/m2；A為梁元截面面積，m2；ρ為材料密度，kg/m3。

對于懸臂梁，邊界條件取為固定端位移和轉角為0，自由端彎矩和剪力為0。懸臂梁第一階彎曲振動固有頻率為[10]：

式中ks為考慮剪應力不均勻分布的系數。

對于懸臂梁，邊界條件取為固定端位移為0，自由端剪力為0。懸臂梁第一階剪切振動固有頻率為：

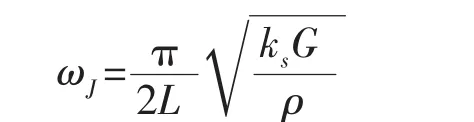
將一階剪切振動固有頻率與一階彎曲振動固有頻率按下式進行耦合，其中f=ω/2π：

式中：f為合成的剪彎振動固有頻率，Hz；fJ為一階剪切振動固有頻率，Hz；fW為一階彎曲振動固有頻率，Hz。

對于船舶上層建筑而言：L取為上層建筑總高度；A取為上層建筑沿高度方向各層截面面積的平均值；I取為上層建筑沿高度方向各層截面慣性矩的平均值，計算過程中只考慮上層建筑的外壁；ks為考慮剪應力不均勻分布的系數，對于矩形截面ks取1/1.2。

采用本文提出的考慮彎曲振動影響的修正系數計算公式計算了12000t貨船、6600TEU集裝箱船、112000t油輪、PANAMAX型油船、31000t散貨船和35000t散貨船六條船的彎曲振動修正系數，同時采用三維有限元方法分別計算了以上六條船的剪彎振動固有頻率，并與利用文獻[1]中公式計算得到的剪切振動固有頻率結果進行比較，得到比例系數，計算結果見表2。

表2 彎曲振動修正系數計算結果Tab.2 Results of the bending vibration correction coefficient

由表2中的計算結果可知，本文方法與三維有限元方法的計算結果較為接近，證明了本文提出的彎曲振動修正系數計算公式的準確性。

2.2 剛體回轉振動固有頻率

文獻[4]中將上層建筑整體視為剛體，并彈性固定在主船體上，上層建筑前端為簡支、后端為彈性支持，其剛體回轉振動固有頻率計算公式如下：

式中： fr為上層建筑剛體回轉振動固有頻率，Hz；ri為上層建筑第i層質量質心到回轉軸的距離，m；k為上層建筑根部的等效剛性系數，N/m；l1為上層建筑最下一層長度，m。

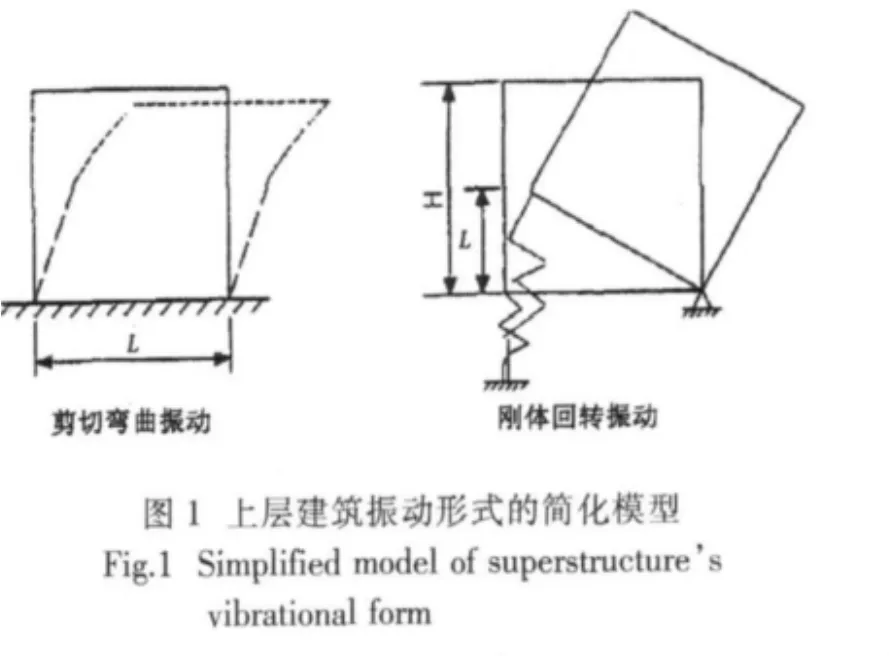
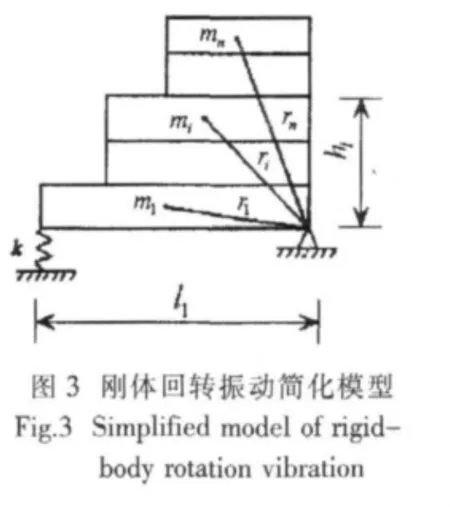
通常上層建筑前壁之下有主船體橫艙壁，上層建筑的后壁落在機艙區，其下一般沒有主船體橫艙壁，其剛體回轉振動簡化成如圖3所示的形式。

對于上層建筑剛體回轉振動固有頻率計算,在上層建筑結構已經確定的情況下，關鍵問題是確定上層建筑后壁根部與主船體連接的等效剛性系數k，目前這個問題尚未得到圓滿的解決。本文利用ANSYS軟件建立了12000t貨船、6600TEU集裝箱船、112000t油輪、PANAMAX型油船、31000t散貨船和35000t散貨船六條船的全船三維有限元模型，確定其等效剛性系數k，將上層建筑前壁與主船體連接處進行約束處理，在上層建筑后壁與主船體連接處施加單位均布載荷，通過計算上層建筑后壁處節點位移與施加的作用力的關系，進而求出等效剛性系數k。

目前船舶多采用機艙和上層建筑布置在艉部的形式，即尾機型或中尾機型，上層建筑與主船體的連接形式簡化為如圖4所示。上層建筑與主船體連接剛度主要取決于主船體的剛度、上層建筑與主船體的連接長度、船體尾部與上層建筑的耦合影響，即上層建筑整體振動時會帶動艉部一起振動。而主船體的剛度主要取決于船體橫剖面慣性矩，船體橫剖面慣性矩可以近似取為I*=cBD2L*，其中：c為常數；B為船寬；D為型深；L*為船長。因此可以取剛度參數為Q=I*l*1/l*c=BD2L*l*1/l*，其中：l*1為上層建筑與主船體的連接長度；l*為因考慮船體尾部與上層建筑的耦合影響而計入的主船體尾部結構長度，通常船體尾部結構是指從艉端至機艙前端橫艙壁這部分結構。

本文計算了六條船的等效剛性系數和剛度參數，計算結果見表3。并以剛度參數Q為橫坐標，等效剛性系數k為縱坐標，采用最小二乘法進行曲線擬合，繪制出等效剛性系數曲線如圖5所示，擬合得到的曲線方程如下：

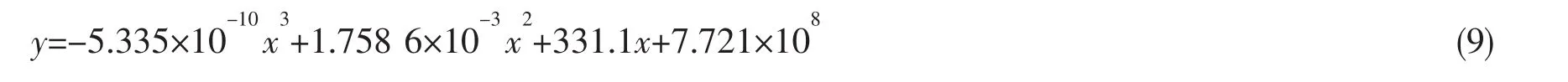
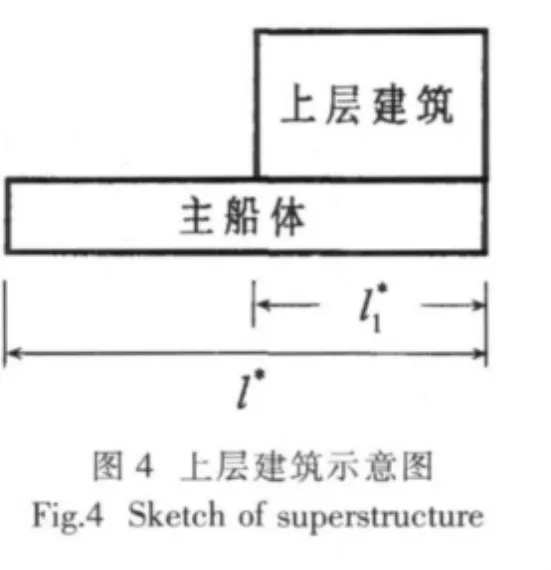
表3 6條船的等效剛性系數計算結果Tab.3 Results of six different ships’equivalent rigid coefficients

對于其它船舶，如果已知剛度參數Q，利用圖5或（9）式可以簡單方便地計算出等效剛性系數k，進而求得上層建筑剛體回轉振動固有頻率。

2.3 上層建筑整體縱向振動固有頻率

為了計算方便將上層建筑整體縱向振動固有頻率計算公式（1）改寫為如下形式：

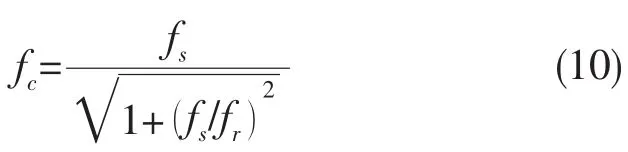
此式即為上層建筑整體縱向振動固有頻率的最終表達式。應用本文提出的方法計算6600TEU集裝箱船、112000t油輪、35000t散貨船、PANAMAX型油船、31000t散貨船和12000t貨船六條船的上層建筑整體縱向振動固有頻率以及剪彎振動固有頻率和剛體回轉振動固有頻率，并與三維有限元方法的計算結果進行了比較，計算結果見表4。由表4中的計算結果可知，本文方法與三維有限元方法的計算結果較為接近。

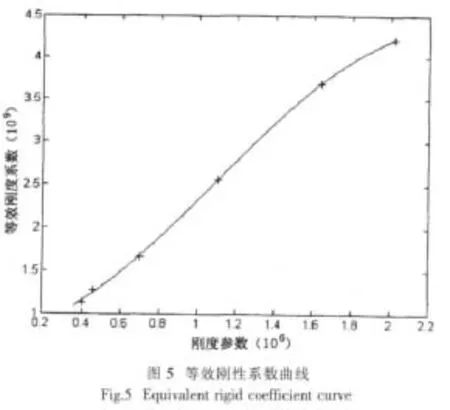
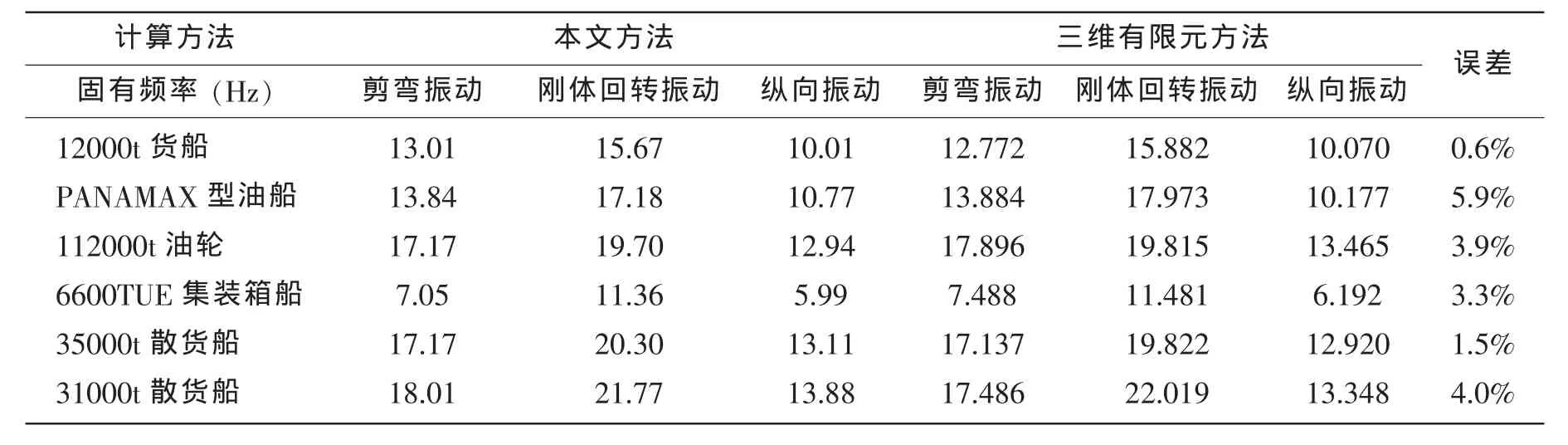
表4 6條船的固有頻率計算結果Tab.4 Natural frequency results of six different ships

3 算例驗證

以52000t大艙口貨船為例，采用本文方法計算其上層建筑整體縱向振動固有頻率，其剛度參數取值為1.20×106m4，計算得到的等效剛性系數為2.75×109N/m，彎曲振動的修正系數0.758，剪彎振動固有頻率為10.86Hz，剛體回轉振動固有頻率為12.16Hz，最終得到的上層建筑整體縱向振動固有頻率為8.10Hz，與實測值8Hz較為接近[12]。

4 結 論

本文推導了上層建筑整體縱向振動固有頻率預報公式，將上層建筑整體縱向振動固有頻率視為由上層建筑根部剛性固定在主船體上的剪彎振動固有頻率和上層建筑根部彈性固定在主船體上的剛體回轉振動固有頻率兩部分串聯合成，重點研究了上層建筑剛體回轉振動固有頻率計算公式中等效剛性系數的取法，并對剪切振動固有頻率計算公式進行了修正，給出了彎曲振動修正系數計算公式。采用三維有限元模型計算了6600TEU集裝箱船、112000t油輪、35000t散貨船、PANAMAX型油船、31000t散貨船和12000t貨船六條船的上層建筑整體縱向振動固有頻率以及剪彎振動固有頻率和剛體回轉振動固有頻率，并且得到了各條船等效剛性系數，繪制了等效剛性系數曲線，根據剛度參數Q，可以簡單方便地計算出等效剛性系數。以52000t大艙口貨船為例，采用本文方法計算其上層建筑整體縱向振動固有頻率，計算結果與實測值較為接近，證明本文提出的方法是可靠的。本文所提出的方法主要適用于油船、散貨船和集裝箱船等上層建筑結構短且高的情況，今后可以搜集大量實船資料，按船舶類型來繪制等效剛性系數曲線，可以使計算結果更精確。

[1]大沼覺,山本鷹司,中野元博,尾上光賢.船尾船橋樓の船樓の振動について[J].西部造船會會報,1969（第38號）:93-120.

[2]馬廣宗,劉健宜,石慈忠.估算船舶上層建筑固有頻率的新方法[J].中國造船,1986(3):56-66.

[3]曹 迪,趙德有,馬廣宗等.船舶上層建筑縱向振動固有頻率估算[J].大連理工大學學報,1989(4):463-469.

[4]趙德有,林 哲.船舶上層建筑整體縱向固有頻率算法研究[J].中國造船,2001(3):22-27.

[5]日本海事協會.船舶振動設計指南[M].1981.

[6]DNV.Prevention of Harmful Vibration in Ship[M].1983.

[7]惲偉君,葉祖英,胥加華.膜梁組合模型的船舶總體與上層建筑耦合振動[J].上海船舶運輸科學研究所學報,1987(1):71-77.

[8]楊 波,薛惠鈺,何 窮.分析船舶上層建筑動力特性的有限元模型研究[J].計算結構力學及其應用,1985(4):61-68.

[9]郭 列,吳士沖,何富堅等.船舶上層建筑有限元計算模型研究[J].振動與沖擊,1996(2):47-52.

[10]張義民.機械振動[M].北京:清華大學出版社,2007.

[11]陸鑫森,金咸定,劉涌康.船體振動學[M].北京:國防工業出版社,1980.

[12]趙德有,唐建生,洪 明等.52000t大艙口多用途貨船有害振動的診斷及治理[J].大連理工大學學報,1998,38(4):438-444.

Study on predicting method of natural frequency for superstructure’s overall longitudinal vibration

YIN Yu-mei,ZHAO De-you
(Department of Naval Architecture,Dalian University of Technology,Dalian 116085,China)

The prediction formula for natural frequency of the superstructure overall longitudinal vibration is derived,natural frequency of the overall longitudinal vibration of superstructure is consisted of two parts:the natural frequency of shearing-bending vibration of superstructure rigidly fixed on the hull and the natural frequency of rigid-body rotation vibration of superstructure elastically fixed on the hull.The algorithm of the equivalent stiffness coefficient for calculating the natural frequency of superstructure with rigid-body rotation vibration is studied.And formula for calculating the natural frequency of shear vibration is amended,also correction coefficient formula of bending deformation is proposed.The natural frequency of longitudinal vibration,the natural frequency of shearing-bending vibration and the natural frequency of rigid rotating vibration of superstructure of six ships including 6600TEU container ship,112000t tankers,35000t bulk carrier,PANAMAX tanker,31000t bulk carrier and 12000t multi-purpose cargo ship are calculated by ANSYS software.And the equivalent rigid coefficient is obtained,and the curve of the equivalent rigid coefficient can be drawn.Taking 52000t big hatch cargo ship for example,the frequency result of superstructure longitudinal vibration calculated by the method proposed in this paper coincides with measured value,thus the method proposed is feasible.

superstructure;natural frequency;bending deformation correction coefficient;equivalent rigid coefficient

殷玉梅（1982-），女，博士生，E-mail:21932937@163.com； 趙德有（1935-2009），男，教授，博士生導師。

U661.44

A

1007-7294（2011）05-0538-07

2010-01-15 修改日期：2011-03-09