積分第一中值定理中間點集穩定性的注記

羅群

（肇慶學院 數學與信息科學學院,廣東 肇慶 526061）

0 引言

在《數學分析》教材中，有如下定理：

積分第一中值定理[1]若f在[a,b]上連續，則至少存在一點ξ∈[a,b]，使得

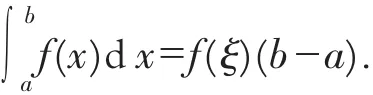
該定理是數學分析中的一個重要定理.稱這樣的點ξ∈[a,b]為連續函數f在區間[a,b]上的中間值點（或平均值點），以下簡稱f的中間點.文獻[2]及其參考文獻中討論了連續函數f的中間值點的漸近性.對于[a,b]上的連續函數f，這樣的中間點不一定是唯一的.本文討論中間點集的穩定性，即當連續函數f發生微小變化時，f的中間點集是否也發生微小變化？有例子表明這個結論是否定的.為此，筆者引入本質中間點等概念討論中間點集的穩定性問題，得到如下結論：[a,b]上大多數連續函數（在Baire分類意義下）的中間點集是穩定的；[a,b]上連續函數的中間點集是本質連通區的一個充分條件.

1 預備知識

設X和Z是2個Hausdorff拓撲空間，F∶Z→2X是集值映射.

定義1 1）稱F在y∈Z處是上半連續的，如果對X中任意開集O且F(y)?O，存在y的開鄰域N(y)，使得對任意y′∈N(y)，有F(y′)?O；稱F在Z上為上半連續的，如果F在任意y∈Z處為上半連續的.

2）稱F在y∈Z處是下半連續的，如果對X中任意開集O且O∩F(y)≠?，存在y的開鄰域N(y)，使得對任意y′∈N(y)，有F(y′)∩O≠?；稱F在Z上為下半連續的，如果F在任意y∈Z處為下半連續的.

3）稱F在Z上是連續的，如果F在Z上既是上半連續又是下半連續的.

4）稱F在Z上是usco映射，如果對任意y∈Z，F(y)是緊值的且F在Z處是上半連續的.

記C[a,b]是定義在閉區間[a,b]上的實值連續函數，對任意f，g∈C[a,b]，定義度量ρ和范數‖·‖如下：

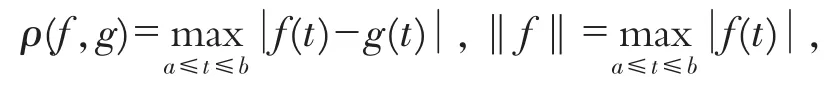
則C[a,b]是Banach空間[3].

對集合A，B?[a,b]，記H(A,B)為[a,b]上的Hausdorff度量.

下面的引理1是Fort定理，參見文獻[4－5].

引理1 如果X是度量空間，Z是Baire空間，F是Z上的usco映射，則存在Z中的稠密剩余集Q，使得對任意y∈Q，F在y處是下半連續的.

2 主要結論

引理2 映射G是一個usco映射，即G是具有緊值且上半連續的集值映射.

證 由于[a,b]是緊的，要證G是緊值的，只需證：對任意f∈C[a,b]，G(f)是閉的.設ξ0是G(f)的聚點，則存在G(f)中的點列，使得

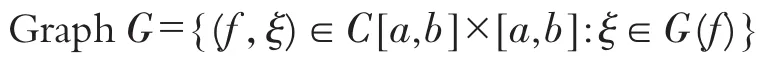
由于

例1 設[a,b]＝[0,1]，f（t）≡1,t∈[0,1]，則G（f）＝[0,1].對任意ε＞0，取則，但G（fε）＝{1/2 }，顯然，即G在f不連續，從而G（f）不穩定.

即(f*，ξ*)∈Graph G，從而映射G是usco映射.

定義2 1）對f∈C[a,b]，稱ξ∈G（f）是f的本質中間點，如果對ξ的任意開鄰域O(ξ)∈[a,b]，存在δ＞0，使得對任意滿足ρ(f，g)＜δ的g∈C[a,b]都有O(ξ)∩G(g)≠?；

2）稱f∈C[a,b]是本質的，如果每個ξ∈G（f）都是f的本質中間點；

3）設f∈C[a,b]，Cα（f）?G（f）是連通子集，稱Cα（f）是G（f）的本質連通區，如果對任意在[a,b]內且包含Cα（f）的開集O，都存在δ＞0，使得對任意滿足ρ(f，g)＜δ的g∈C[a,b]，都有O∩G(g)≠?；

4）稱f∈C[a,b]的中間點集G（f）是穩定的，如果G在f處是連續的.

由定義1及定義2易得下面的定理1.

定理1 映射G在f∈C[a,b]處下半連續的充要條件為f是本質的.（證明省略）

由引理1、引理2和定理1可得到定理2.

定理2 存在C[a,b]中一個稠密剩余集Q，使得對任意f∈Q?C[a,b]，G在f處是下半連續的.從而f∈Q是本質的，G在f處是連續的，即G（f）是穩定的.（證明省略）

由定理2可知，仍有f∈C[a,b]，而G在f處不是連續的，即G（f）是不穩定的.

例1說明，當C[a,b]中的連續函數f有微小變化時，f的中間點集G(f)發生較大變化，即中間點集不穩定.盡管不能得到G(f)是穩定的，但可以得到G(f)存在本質連通區的一個充分條件.

定理3 對f∈C[a,b]，若G(f)＝[α,β]?[a,b]，則G(f)是本質連通區.

證 （反證法）假設G(f)不是本質連通區，則存在開集O*?G(f)，使得對任意n＝1,2,3,…，存在gn∈C[a,b]，ρ(f，gn)＜1/n,滿足G(gn)∩O*＝?.

對任意n＝1,2,3,…，取xn∈G(gn)，則xn?O*.由于｛xn｝?[a,b]，所以｛xn｝有聚點x*?[a,b].不妨設而所以f(x*)(b－a)＝于是x*∈G(f)＝[α,β]?O*，而O*為開與xn?O*矛盾.故G(f)是本質連通區.

推論1 對f∈C[a,b]，若G(f)是單點集｛x0｝，則x0是f的本質中間點，此時G在f處是連續的.

注1 對f∈C[a,b]，若G(f)不是單點集，則f可能沒有本質中間點.

例2 設[a,b]＝[0,1]，f(t)≡0,t∈[0,1]，則G(f)＝[0,1]不是單點集.下面證明f沒有本質中間點.

事實上，對任意x0∈[0,1].若x0∈(0,1)，取充分小的δ＞0，使得(x0－4δ,x0＋4δ)?(0,1).對任意ε＞0，取

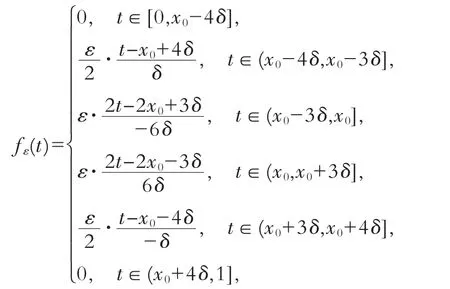
同理可證x0＝0與x0＝1也不是f的本質中間點，故f沒有本質中間點.

[1] 華東師范大學數學系.數學分析:上冊[M].3版.北京:高等教育出版社，2005:217.

[2] 張新元,王驍力.一類函數第一積分中值定理中值點的漸近性[J].數學的實踐與認識,2011,41(4):228-233.

[3] 泛函分析引論及應用[M].張石生，等譯.重慶:重慶出版社,1986:57.

[4] FORT M K J.Points of continuity of semicontinuous functions[J].Publ Math Debrecen,1952(2):100-102.

[5] 羅群，俞建.擬變分不等式解集的極小本質集及其應用[J].高校應用數學學報:A輯,2004,19(1):81-88.