一種用于無線傳感器網(wǎng)絡(luò)節(jié)點(diǎn)遞增式定位的新方法*

熊偉麗，唐蒙娜，徐保國

(江南大學(xué)輕工過程先進(jìn)控制教育部重點(diǎn)實(shí)驗(yàn)室，江蘇無錫214122)

無線傳感器網(wǎng)絡(luò)技術(shù)作為一種新的信息獲取和處理技術(shù)，具備傳統(tǒng)技術(shù)不可比擬的優(yōu)勢，在軍事和民用領(lǐng)域擁有廣闊的應(yīng)用前景。正確的節(jié)點(diǎn)定位是無線傳感器網(wǎng)絡(luò)構(gòu)建和維護(hù)、監(jiān)測定位、目標(biāo)跟蹤等功能實(shí)現(xiàn)的前提和基礎(chǔ)［1］。目前用的較多的節(jié)點(diǎn)定位方法是最小二乘法、加權(quán)最小二乘法等，然而最小二乘法雖然考慮了參考節(jié)點(diǎn)的定位誤差，但沒有考慮到遞增式定位方法中不同級的參考節(jié)點(diǎn)定位誤差的不同［4－5］;加權(quán)最小二乘法雖然考慮了各級參考節(jié)點(diǎn)的定位誤差的不同，但其權(quán)值的確定不能使節(jié)點(diǎn)定位達(dá)到最優(yōu)。

本文延續(xù)遞增式模型中不同級參考節(jié)點(diǎn)定位誤差不同的特點(diǎn)，針對加權(quán)最小二乘法中權(quán)值選取的不足，提出最優(yōu)加權(quán)最小二乘法對該問題進(jìn)行改進(jìn)，在估計(jì)誤差方差矩陣最小時(shí)取得最優(yōu)權(quán)值，最終得到最優(yōu)估計(jì)解。該方法能使節(jié)點(diǎn)的估計(jì)坐標(biāo)與真實(shí)坐標(biāo)間的誤差保持在一個(gè)較穩(wěn)定狀態(tài)，同時(shí)也使誤差減小，確保后級節(jié)點(diǎn)定位的準(zhǔn)確性，盡量減小遞增誤差帶來的影響。仿真結(jié)果表明，最優(yōu)加權(quán)最小二乘在遞增式節(jié)點(diǎn)定位中具有明顯的優(yōu)越性。

1 遞增式定位與累積誤差的形成

按照節(jié)點(diǎn)定位的先后次序不同，定位方法可分為遞增式定位法與并發(fā)式定位法。并發(fā)式定位法中所有節(jié)點(diǎn)同時(shí)進(jìn)行位置計(jì)算，要求錨節(jié)點(diǎn)通信范圍較大，適用于小型傳感器網(wǎng)絡(luò)。當(dāng)網(wǎng)絡(luò)中節(jié)點(diǎn)較多、覆蓋范圍較廣時(shí)采用遞增式定位法較為合理［6－7］。為了降低成本，應(yīng)減小WSN中錨節(jié)點(diǎn)所占的比例，但同時(shí)也降低了定位節(jié)點(diǎn)覆蓋率。為了提高定位節(jié)點(diǎn)的覆蓋率，將已定位節(jié)點(diǎn)升級為參考節(jié)點(diǎn)，利用參考節(jié)點(diǎn)迭代定位將定位節(jié)點(diǎn)的范圍逐步擴(kuò)展到整個(gè)網(wǎng)絡(luò)，這就是遞增式定位法［8］。錨節(jié)點(diǎn)為能夠通過GPS直接定位的節(jié)點(diǎn)。

遞增式定位法引入了誤差累積的問題，參考節(jié)點(diǎn)本身可能存在較大的位置誤差，由于測距誤差和參考節(jié)點(diǎn)位置誤差同時(shí)作用，在下一輪的定位估計(jì)中引入了更大的誤差，當(dāng)網(wǎng)絡(luò)規(guī)模較大時(shí)，誤差累積造成的位置誤差將不容忽視［2，9－10］。遞增式定位方法中，被定義為同一級節(jié)點(diǎn)的定位是同時(shí)進(jìn)行的。假設(shè)目標(biāo)節(jié)點(diǎn)與定位節(jié)點(diǎn)之間的距離已獲得，且測距誤差與距離有關(guān)，建立一個(gè)模擬無線傳感器網(wǎng)絡(luò)來對遞增式定位中的累積誤差進(jìn)行分析［3，11］。圖 1 中，假設(shè) S1、S2、S3為錨節(jié)點(diǎn)，節(jié)點(diǎn)A～E為待定位的未知節(jié)點(diǎn)。連線表示在通信范圍內(nèi)的節(jié)點(diǎn)，圖中線段長度不代表距離。設(shè)錨節(jié)點(diǎn)為零級節(jié)點(diǎn)，一級節(jié)點(diǎn)是指只由錨節(jié)點(diǎn)直接定位的節(jié)點(diǎn)A;只由一級節(jié)點(diǎn)定位或由錨節(jié)點(diǎn)和一級節(jié)點(diǎn)共同定位的節(jié)點(diǎn)C稱為二級節(jié)點(diǎn);以此類推，B、D為三級節(jié)點(diǎn)，E為四級節(jié)點(diǎn)。假設(shè)錨節(jié)點(diǎn)定位無誤差，由前面提到的遞增模式可知，后級節(jié)點(diǎn)的定位誤差通常都大于其前級節(jié)點(diǎn)，節(jié)點(diǎn)定位誤差隨著定位的逐級進(jìn)行呈現(xiàn)增大的趨勢。因此，各節(jié)點(diǎn)誤差大小關(guān)系為:S1、S2、S3＜A ＜C ＜B、D ＜E。為了解決誤差累積問題，引入最優(yōu)加權(quán)最小二乘估計(jì)的方法，在最小二乘估計(jì)中加入最優(yōu)權(quán)值，使定位誤差方差達(dá)到最小，提高定位精度。

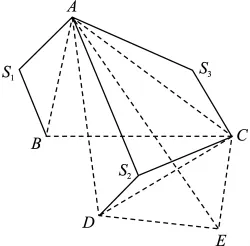
圖1 網(wǎng)絡(luò)中的節(jié)點(diǎn)

2 最優(yōu)加權(quán)最小二乘的節(jié)點(diǎn)定位方法

改進(jìn)的最優(yōu)加權(quán)最小二乘法相對于其他普通的加權(quán)最小二乘，不僅考慮了不同級節(jié)點(diǎn)誤差因子的差異，并在估計(jì)誤差的方差矩陣E［(－H)(－H)T］達(dá)到最小時(shí)取得權(quán)值，能使為真值H的最優(yōu)估計(jì)。下面分別對一級節(jié)點(diǎn)、二級及二級以上節(jié)點(diǎn)的定位進(jìn)行分析。

2．1 一級節(jié)點(diǎn)定位

在本段中，對無線傳感器節(jié)點(diǎn)定位算法進(jìn)行建模，列出方程，針對傳統(tǒng)的加權(quán)最小二乘法存在的估計(jì)有偏問題，列出使估計(jì)最優(yōu)的兩個(gè)條件，引入最優(yōu)加權(quán)最小二乘法，不僅得出對節(jié)點(diǎn)位置的最優(yōu)估計(jì)，且此最優(yōu)估計(jì)無偏。

在實(shí)際無線傳感器網(wǎng)絡(luò)中，各級節(jié)點(diǎn)都可能有無數(shù)個(gè)。假設(shè)網(wǎng)絡(luò)中零級節(jié)點(diǎn)坐標(biāo)為Si(Xsi，Ysi)，且不存在位置誤差，一級節(jié)點(diǎn)坐標(biāo)為A(XA，YA)，測得待定位節(jié)點(diǎn)A到各零級節(jié)點(diǎn)的距離為dsi，其中測距誤差εi1與節(jié)點(diǎn)間距離成比例，獨(dú)立且服從方差為高斯分布，則可建立如下方程組:

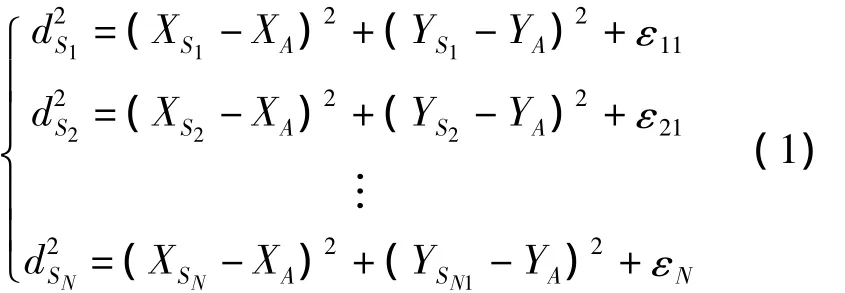
從方程組(1)的第一個(gè)方程開始分別減去最后一個(gè)方程，所得的方程組表示為矩陣形式:

式中:

本文針對上述問題提出最優(yōu)加權(quán)最小二乘法，其核心是找到最優(yōu)的權(quán)系數(shù)陣W，使其估計(jì)誤差的方差矩陣達(dá)到最小，并且為無偏估計(jì)。推導(dǎo)如下:

估計(jì)誤差為:

式中:Kij是相關(guān)系數(shù)，由于各測距誤差不相關(guān)，當(dāng)i≠j時(shí)，Kij=0。

在一級節(jié)點(diǎn)的定位中，權(quán)值取值的不同主要取決于測距誤差的不同。上面計(jì)算的權(quán)值是在方程作差的基礎(chǔ)上取得的。因此，要了解各參考節(jié)點(diǎn)的權(quán)值，需再組建一個(gè)簡單方程組，經(jīng)過計(jì)算得到各節(jié)點(diǎn)的權(quán)值，且各權(quán)值略小于1。

2．2 二級及二級以上節(jié)點(diǎn)定位

由于無線傳感器節(jié)點(diǎn)間存在距離測量誤差，造成一級節(jié)點(diǎn)的定位有誤差，而這些存在誤差的節(jié)點(diǎn)將被后一級節(jié)點(diǎn)作為參考節(jié)點(diǎn)來對自身進(jìn)行定位。由于參考節(jié)點(diǎn)受本身的定位誤差和距離測量誤差的影響，后一級節(jié)點(diǎn)的定位誤差呈現(xiàn)增大的趨勢。要提高節(jié)點(diǎn)的定位精度，除了提高距離測量精度外，還需減小參考節(jié)點(diǎn)定位誤差的影響。

如圖1所示C為二級節(jié)點(diǎn)，其參考節(jié)點(diǎn)包括兩個(gè)零級參考節(jié)點(diǎn)和一個(gè)一級節(jié)點(diǎn)。由于一級節(jié)點(diǎn)受距離測量誤差影響，其估計(jì)位置必然存在誤差，因此一級節(jié)點(diǎn)的定位誤差大于零級參考節(jié)點(diǎn)的定位誤差，根據(jù)不同節(jié)點(diǎn)對C節(jié)點(diǎn)精確定位的影響大小，賦予不同的權(quán)值。

對于二級及二級以上的節(jié)點(diǎn)，其參考節(jié)點(diǎn)存在不同程度的定位誤差，設(shè)各參考節(jié)點(diǎn)定位誤差εi2符服從高斯分布，設(shè)其均值為零，方差為σ2il。由于測距誤差εi1也服從高斯分布，因此εi1+εi2仍服從高斯分布，方程組可表示為:

在定位級數(shù)為二級以及二級以上的待定位節(jié)點(diǎn)時(shí)，由于參考節(jié)點(diǎn)可能是不同級的，而各級的定位精度不同，賦予的權(quán)值也各不同，甚至有較大差異。參考節(jié)點(diǎn)中，除了錨節(jié)點(diǎn)權(quán)值略小于1，而對于其它節(jié)點(diǎn)，由于存在節(jié)點(diǎn)位置本身的定位誤差，其權(quán)值都小于1，且級數(shù)越高，其本身誤差越大，越不利于后級節(jié)點(diǎn)的正確定位，對應(yīng)的權(quán)值也越小。

3 誤差分析

當(dāng)只存在測距誤差，各級參考節(jié)點(diǎn)的定位誤差沒有顯著差別，即測距誤差對各級節(jié)點(diǎn)的影響大致相同;當(dāng)只存在參考節(jié)點(diǎn)定位誤差時(shí)，后級節(jié)點(diǎn)的定位誤差明顯大于前級節(jié)點(diǎn)。在遞增式定位過程中，各級節(jié)點(diǎn)定位誤差來源于測距誤差與參考節(jié)點(diǎn)的定位誤差，因此存在嚴(yán)重的累積誤差，在相同測距誤差的情況下，累積誤差主要是由節(jié)點(diǎn)的定位誤差決定的，如圖2所示。

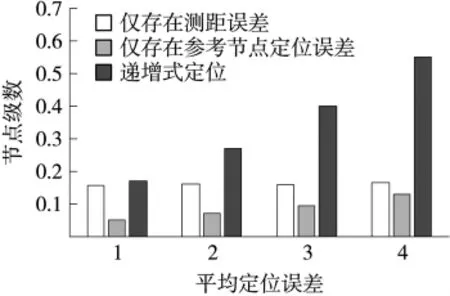
圖2 三種情況下的定位誤差對比圖

每條路徑的測距誤差與其路徑長度有關(guān)，路徑最短的測距誤差服從獨(dú)立的高斯分布 N(0，σ2)。假設(shè)待定節(jié)點(diǎn)共K個(gè)，第i個(gè)待定位節(jié)點(diǎn)的真實(shí)坐標(biāo)為(Xi，Yi)，而根據(jù)本文所運(yùn)用的定位算法得到的定位坐標(biāo)為(i，i)，i=0，1，2，…，K。定義節(jié)點(diǎn)定位誤差為節(jié)點(diǎn)的真實(shí)位置與估計(jì)位置間的距離與通信距離D之比各級節(jié)點(diǎn)平均定位誤差為同級節(jié)點(diǎn)定位誤差之和除以節(jié)點(diǎn)數(shù)。

本文利用的最優(yōu)加權(quán)最小二乘可以盡量減小累積誤差帶來的問題，通過計(jì)算給不同級節(jié)點(diǎn)引入了不同的權(quán)值，誤差越大的節(jié)點(diǎn)對正確定位越不利，相應(yīng)的權(quán)值就越小，并賦予了結(jié)果對誤差方差最優(yōu)的特點(diǎn)。下一節(jié)對改進(jìn)方法進(jìn)行仿真分析與對比。

4 仿真與對比

以100 m×100 m的正方形農(nóng)田為單位部署100個(gè)節(jié)點(diǎn)，將節(jié)點(diǎn)射頻通信距離設(shè)為15 m，測距精度使用相對誤差表示，即誤差占射頻通信距離的比例，測距誤差服從高斯分布。部署于農(nóng)田中的無線傳感器節(jié)點(diǎn)的主要功能是采集節(jié)點(diǎn)周圍的土壤信息，如溫度、濕度及土壤緊實(shí)度等。

仿真階段必須選擇出合理的權(quán)值，使定位誤差達(dá)到最小。加權(quán)最小二乘法中，為了取得能使定位誤差達(dá)到相對小的權(quán)值，需多次取值進(jìn)行結(jié)果對比。最優(yōu)加權(quán)最小二乘法較加權(quán)二乘法的最大優(yōu)勢是權(quán)值能根據(jù)方差陣的逆陣來取得最高精度的估計(jì)值，結(jié)果同樣遵循級數(shù)越高，權(quán)值越小的原則。測距誤差增大時(shí)，要達(dá)到最小定位誤差，權(quán)值有相應(yīng)的減小，但這種減小的趨勢不明顯，即測距誤差的影響不占主導(dǎo)作用，影響主要是由參考節(jié)點(diǎn)的位置誤差造成的。圖3為參考節(jié)點(diǎn)定位誤差ε的方差取不同值時(shí)的平均誤差圖。

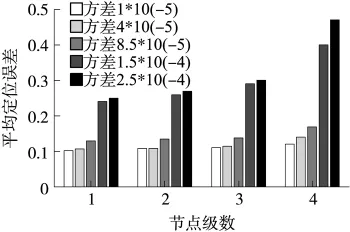
圖3 ε方差不同時(shí)各級節(jié)點(diǎn)平均定位誤差對比圖

由圖3可知，ε取不同值時(shí)，各級節(jié)點(diǎn)平均定位誤差各不同。ε的方差越大，節(jié)點(diǎn)平均定位誤差也越大。在測距誤差為1%時(shí)，由于測距誤差在距離的±1%間呈正態(tài)分布，因此其節(jié)點(diǎn)位置誤差也有變化。圖4是ε的方差一定時(shí)，應(yīng)用最小二乘法、加權(quán)最小二乘法和最優(yōu)加權(quán)最小二乘法所得到的待定位節(jié)點(diǎn)誤差的對比圖。

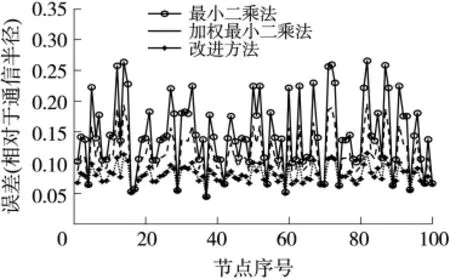
圖4 測量誤差一定時(shí)不同算法的誤差對比圖

從圖4中的對比可以看出，應(yīng)用最優(yōu)加權(quán)最小二乘法得到的定位誤差明顯低于最小二乘法和加權(quán)最小二乘法，對節(jié)點(diǎn)的正確定位具有有效的改進(jìn)作用。另外由圖可知，不管用何種方法，同一點(diǎn)處的定位誤差呈現(xiàn)相同的趨勢，即低級節(jié)點(diǎn)的定位誤差小于高級節(jié)點(diǎn)，也驗(yàn)證了本文方法的正確性。

5 結(jié)束語

本文根據(jù)遞增式定位方法的特點(diǎn)，提出最優(yōu)加權(quán)最小二乘的方法來改進(jìn)遞增式節(jié)點(diǎn)定位中的缺陷，通過不同測距誤差下定位誤差大小的對比，在一個(gè)相對最小的測距誤差下，運(yùn)用最優(yōu)加權(quán)最小二乘法與運(yùn)用其他定位方法進(jìn)行MATLAB仿真對比。從仿真結(jié)果可以看出，該方法能有效抑制無線傳感器定位迭代循環(huán)過程中誤差累積的影響，使遞增式節(jié)點(diǎn)定位方法能夠越來越廣泛的應(yīng)用于無線傳感器網(wǎng)絡(luò)的定位中。

［1］ 曹曉梅，俞波．傳感器網(wǎng)絡(luò)節(jié)點(diǎn)定位系統(tǒng)安全性研究［J］．軟件學(xué)報(bào)，2008，9(4):869 －877．

［2］ 王建剛，王福豹，段渭軍．加權(quán)最小二乘估計(jì)在無線傳感器網(wǎng)絡(luò)定位中的應(yīng)用［J］．計(jì)算機(jī)應(yīng)用研究，2006，(9):41 －42．

［3］ 嵇瑋瑋，劉中．遞增式傳感器節(jié)點(diǎn)定位方法的累積誤差分析及其改進(jìn)［J］．南京理工大學(xué)學(xué)報(bào)，2008，32(4):496 －501．

［4］ 范偉軍，周必方，夏良正等．基于最小二乘法準(zhǔn)則的光學(xué)綜合孔徑觀測目標(biāo)傅里葉信息提取［J］．光子學(xué)報(bào)，2004，33(4):72－475．

［5］ 包志華，周暉，邵世煌．基于智能估計(jì)的無線傳感器網(wǎng)絡(luò)定位算法［J］．傳感技術(shù)學(xué)報(bào)，2008，21(10):1755 －1769．

［6］ Hwang S，Willians D B．A Constrained Total Least Square Approach for Sensor Position Calibration and Direction Finding［C］//Proc of the IEEE National Radar Conference．USA，1994:155 －159．

［7］ Huang Z，Lu J．Total Least Square and Equilibration Algorithm for Range Difference Location［J］．Electronics Letter，2004，40(5):121 －122．

［8］ Savvides A，Han C C，Srivastava M B．Dynamic Fine-Grained Localization in Ad-Hoc Networks of Sensors［C］//Proc of 7th Annual International Conf on Mobile Computing and Networking(MobiCom)．USA，2001:166－179．

［9］ 魏葉華，李仁發(fā)，羅娟，等．基于支持向量回歸的無線傳感網(wǎng)絡(luò)定位算法［J］．通信學(xué)報(bào)，2009，30(10):44 －50．

［10］黃浩，盧文科．無線傳感器網(wǎng)絡(luò)中基于錨節(jié)點(diǎn)反饋的多跳測距定位算法改進(jìn)［J］．傳感技術(shù)學(xué)報(bào)，2009，22(2):269 －272．

［11］ C K Chui，G Chen．Kalman Filtering with Real-Time Applications［M］．Springer-Verlag，1987．

［12］ CostaJ A，Patwari N，Hero A O．Distributed Weighted Multidimensional Scaling for Node Localization in Sensor Networks［J］．ACM Transactions on Sensor Networks，2006，2(1):1 －26．

［13］ Niculescu D，Nath B．DV Based Positioning in Ad Hoc Networks［J］．Telecommunication systems-Modeling，Analysis，Design and Management，2003，22(1/4):267 －280．